Unit - 2

Principles of Mathematical Induction

Q1) Define principle of mathematical induction.

A1)

Mathematical induction is a mathematical technique is used to prove a statement, a theorem or a formula is true for every natural number.

The technique has two steps to prove any statement-

1. Base step (it proves that a statement is true for the initial value)

2. Inductive step (it proves that is the statement is true for n’th iteration then it is also true for iteration.

Q2)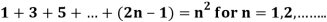

A2)

Here for n = 1,     1 = 1²

Now let us assume that the statement is true for n = k

Hence we assume that 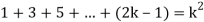is true.

Now we need to prove that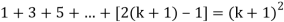

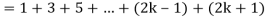
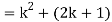
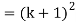
So that 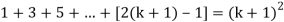which satisfies the second step.

Hence-

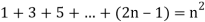
Q3) Prove 1+2+...+n = n(n+1)/2 using a proof by induction.

A3)

Let n=1: 1 = 1(1+1)/2 = 1(2)/2 = 1 is true,

Step-1: Assume n=k holds: 1+2+...+k = k(k+1)/2

Show n=k+1 holds: 1+2+...+k+(k+1)=(k+1)((k+1)+1)/2 

Substitute k with k+1 in the formula to get these lines. Notice that I write out what I want to prove.

Step-2: Now start with the left side of the equation

1+2+...+(k+1)=1+2+...+k+(k+1)

=k(k+1)/2 + (k+1)

=(k(k+1)+2(k+1))/2 by 2/2=1 and distribution of division over addition

=(k+2)(k+1)/2 by distribution of multiplication over addition

=(k+1)(k+2)/2 by commutativity of multiplication

Q4) Prove the following by using the principle of mathematical induction for all n ∈ N-

A4)

Here, n = 1, 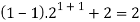, which is true

Step-1: Assume n = k holds-

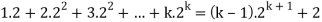
Now show n = k + 1 also holds-

Consider-

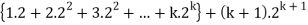
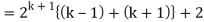
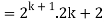
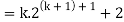
Which is also true for n = k + 1.

Hence proved.

Q5) What is Pigeonhole principle?

A5)

If n pigeonholes are occupied by n + 1 or more pigeons, then at least one pigeonhole is occupied by more than one pigeon.

This principle can be applied to many problems where we want to show that a given situation can occur.

Example: Suppose a class contains 13 students, then two of the students (pigeons) were born in the same months (pigeonholes)

Q6) Show that if seven numbers from 1 to 12 are chosen, then two of them will add up to 13.

A6)

First we will construct six different sets, each containing two numbers that add up to 13 as follows-

= {1, 12}, 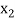= {2, 11}, = {3, 10}, = {4, 9}, 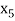= {5, 8}, 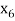= {6, 7}.

Each of the seven numbers belong to one of these six sets.

Since there are six sets, then according to the pigeonhole principle that two of the numbers chosen belong to the same set. These numbers add upto 13.

Q7) What do you understand by Generalized pigeonhole principle?

A7)

If n pigeonholes are occupied by kn+ 1 or more pigeons, where k is a positive integer, then at least one pigeonhole is occupied by k + 1 or more pigeons.

Q8) Find the number of students at a college choosing at least one of the subject from mathematics, physics and statistics.

The data is given as-

65 study maths, 45 study physics, 42 study statistics, 20 study maths and physics, 25 study maths and statistics, 15 study physics and statistics and 8 study all the three subjects.

A8)

Here we need to find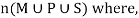

Now by using Inclusion-Exclusion principle-

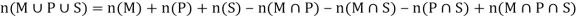
Which gives-

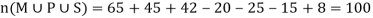
Therefore, we find that 100 students study at least one of the three subjects.

Q9) Define relatively prime integers.

A9)

Two integers a and b are said to be relatively prime or coprime if gcd(a, b) = 1. Accordingly, if a and b are relatively prime, then there exist integers x and y such that ax + by = 1

Conversely, if ax + by = 1, then a and b are relatively prime.

Example: Observe that: gcd(12, 35) = 1, gcd(49, 18) = 1, gcd (21, 64) = 1, gcd (−28, 45) = 1

Q10) What is fundamental Theorem of Arithmetic?

A10)

Every integer n >1 can be expressed uniquely (except for order) as a product of primes.

The primes in the factorization of n need not be distinct. Frequently, it is useful to collect together all equal primes. Then n can be expressed uniquely in the form

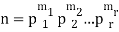
Where the mi are positive and p1 < p2 < ... < pr . This is called the canonical factorization of n.

Q11) Explain permutation.

A11)

The arrangement of a set of n objects in a given order is called a permutation.

Any arrangement of any of these objects in a given order is said to be r-permutation.

The number of permutations of n objects taken r will be denoted as-

P(n, r)

Formula-                                          

Permutation with repetitions-

The number of permutations of n objects of which are 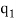are alike, are alike,

Are alike is-

Q12) There are 4 black, 3 green and 5 red balls. In how many ways can they be arranged in a row?

A12)

Total number of balls = 4 black + 3 green + 5 red = 12

The black balls are alike,

The green balls are, and the red balls are alike,

The number of ways in which the balls can be arranged in a row =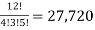

Q13) What are circular permutations?

A13)

A circular permutation of n objects is an arrangement of the objects around a circle.

If the n objects are to be arranged round a circle we take an objects and fix it in one position.

Now the remaining (n – 1) objects can be arranged to fill the (n – 1) positions the circle in (n – 1)! ways.

Hence the number of circular permutations of n different objects = (n – 1)!

Q14) Find the number of non-negative integral solutions to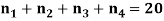

A14)

We have n = 4, r = 20

The number of non-negative integral solutions

= C (4 – 1 + 20, 20)

= C (23, 20)

= 1,771

Q15) In how many ways can a person invite one or more of his 5 friends to a party?

A15)

For every friend there are two possibilities i.e., he may be invited or he may not be invited to attend the party.

The number of ways in which we can invite his five friends at a party is 25.

But this includes the case when none of his friend is invited.

Hence, the number of ways in which he invites one or more of his five friends to a party is

– 1 = 32 – 1 = 31

Q16) Prove that C (n, r) = C (n, n – r).

A16)

C (n, r) denotes the number of selections of n objects when r-things are selected, and the remaining (n – r) objects are not selected. Therefore, selecting of r-things is the same as discarding (n – r) objects. For each selection of r things i.e., for each r-combination there is a discarding of n – r, remaining objects. The number of ways in which we discord (n – r) objects is C (n, n – r).

Since the set of r-combinations and the set of discarding of (n – r) objects are in one-one corresponding we get

C (n, r) = C (n, n – r)

Q17) Show that C (n, 0) + C (n, 1) + … + C (n, n) =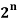

A17)

This is equivalent to finding the number of subsets of a set A with n elements. The number of subsets of A can be considered as follows:

The number of subsets having no elements (i.e., subsets with 0 elements is C (n, 0)

The number of subsets having 1 elements is C (n, 1) …

The number of subsets with n elements is C (n, n). Adding we get the number of elements in the power set of A.

i.e., | (A) | = C (n, 0) + C (n, 1) + … + C (n, n)

But the number of elements in the power set of A is .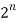

Hence C (n, 0) + C (n, 1) + … + C (n, n) =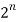

Q18) A farmer buys 4 cows, 2 goats and 5 ducks from a person who has 7 cows, 5 goats and 8 ducks. How many choices the farmer has:

A18)

The farmer can choose 4 cows from 7 cows in C (7, 4) ways, 2 goats from 5 goats in C (5,

2) ways and 5 ducks from 8 ducks in C (8, 5) ways.

∴ The farmer can choose 4 cows, 2 goats and 5 ducks in C (7, 4) C (5, 2) C (8, 5)

Q19) Find the term containing 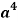in the expansion of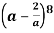

A19)

The general term will be-

Tr+1 = C(8, r) a8-r(-2/a)r

= C (8, r) a8-r(-2a-1)r

= C (8, r) a8-r (-2)r(a-1)r

= C(8, r) (-2)r a8-ra-r

= C (8, r)(-2)r a8-2r

Put 8 – 2r = 4 we get r = 2

Therefore the term contains is-

Tr+1 = T3 = C (8, r)(-r)ra4

= C(8, r) 4 a4

= 28 4 a4

= 112 a4

Q20) Prove that

A20)

We know that

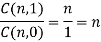
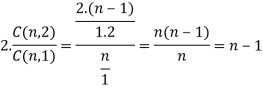
Adding, we get

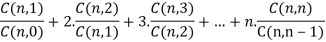
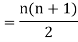
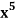
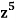
Q21) Find the coefficients of 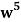in the expansion of .

A21)

We have n = 25, x1 = x1, x2 = 74, x3 = 3 z, and x4 = w

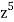
∴ The coefficients of   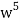in the expansion of .

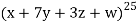Is

Q22) Check whether is a solution to the recurrence relation 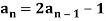with .

A22)

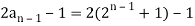
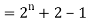
Q23) Solve the recurrence relation-

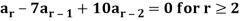
A23)

Multiplying each term of the recurrence relation by , we find-

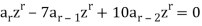
Now taking the sum to 2 to , we get

Replace each infinite sum by the corresponding equivalent expression given above, we obtain-

[A(z) – a0 – a1 z] – 7 z [ A(z) – a0] – 10 z2 A(z) = 0

On simplifying, we obtain-

A(z) (1 – 7z + 10 z2 ] = a0 + a1 z – 7a0z

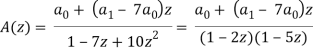
Decomposing A (z) as a sum of partial fractions, we can write

The solution is-