Unit - 1
Review of Algebraic and Order Properties of R
Q1) What are the properties of the addition of real numbers?
A1)
The properties of the addition of real numbers are
- x + y = y + x for x, y
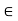 R. (Commutativity of Addition)
R. (Commutativity of Addition) - (x + y) + z = x + (y + z) for all x, y, z
 R. (Associativity of Addition)
R. (Associativity of Addition) - There exists a unique element 0
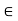 R such that x + 0 = 0 + x = x for all x
R such that x + 0 = 0 + x = x for all x  R. (Existence of Additive Identity or Zero)
R. (Existence of Additive Identity or Zero) - For every x
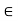 R, there exists a unique element y
R, there exists a unique element y  R such that x + y = 0 We denote this y by -x. (Existence of Additive Inverse)
R such that x + y = 0 We denote this y by -x. (Existence of Additive Inverse)
Q2) What are the properties of the multiplication of real numbers?
A2)
The properties of the multiplication of real numbers are
- x . y = y . x for all x, y
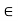 R. (Commutativity of Multiplication)
R. (Commutativity of Multiplication) - x . (y . z) = (x . y) . z for all x, y, z
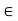 R. (Associativity of Multiplication)
R. (Associativity of Multiplication) - There exists a unique element 1
 R such that x . 1 = 1 . x = x for all x
R such that x . 1 = 1 . x = x for all x 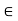 R. (Existence of Multiplicative Identity)
R. (Existence of Multiplicative Identity) - Given x
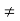 0 in R, there exists a unique y such that xy = 1 = yx.We denote this y by 1/x or
0 in R, there exists a unique y such that xy = 1 = yx.We denote this y by 1/x or 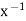 (Existence of Multiplicative Inverse or Reciprocal)
(Existence of Multiplicative Inverse or Reciprocal)
Q3) What is called ε-neighborhood of a point in R?
A3)
Let a  R and
R and 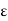 > 0. Then the
> 0. Then the 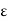 -neighborhood of a is the set-
-neighborhood of a is the set-
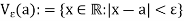
For a 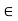 R, the statement that x belongs to
R, the statement that x belongs to 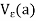 is equivalent to either of the statements
is equivalent to either of the statements


Q4) Define ordered field.
A4)
We defined the order relation 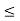 in R. It is easy to see that this order relation satisfies the following properties:
in R. It is easy to see that this order relation satisfies the following properties:
Let x, y, z be any elements of R. Then
O1: For any two elements x and y of R, one and only of the following holds:
(i) x < y, (ii) y < x, (iii) x = y,
O2: x  y, y
y, y 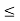 x implies x
x implies x 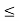 z,
z,
O3: x 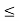 y implies x
y implies x 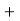 z
z  y + z,
y + z,
O4: x  y, 0 < z implies x.z
y, 0 < z implies x.z 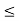 y.z
y.z
Q5) What do you understand by complete ordered field?
A5)
Although R and Q are both ordered fields, yet there is a property associated with the order relation which is satisfied by R but not by Q. This property is known as the Order-Completeness, introduced for the first time by Richard Dedekind.
Suppose set S = {1, 3, 5, 7). You can see that each element of S is less than or equal to 7. That is x 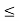 7, for each x
7, for each x 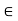 S. Take another set S, where S = {x
S. Take another set S, where S = {x 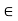 R : x
R : x  17). Once again, you see that each element of S is less than 18. That is, x < 18, for each x
17). Once again, you see that each element of S is less than 18. That is, x < 18, for each x 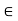 S. In both the examples, the sets have a special property namely that every element of the set is less than or equal to some number.
S. In both the examples, the sets have a special property namely that every element of the set is less than or equal to some number.
Q6) What is upper bound?
A6)
Let S  R. If there is a number u
R. If there is a number u 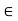 R such that x
R such that x  u, for every x
u, for every x  S, then S is said to be bounded above. The number u is called an upper bound of S.
S, then S is said to be bounded above. The number u is called an upper bound of S.
Q7) What are bounded sets?
A7)
A set S is bounded if it is both bounded above and bounded below.
In other words, S has an upper bound as well as a lower bound. Thus, if S is bounded, then there exist numbers u (an upper bound) and v (a lower bound) such that v 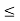 x
x 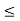 u, for every x
u, for every x 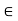 S.
S.
If a set S is not bounded then S is called an unbounded set. Thus S is unbounded if either it is not bounded above or it is not bounded below.
Q8) What is called Supremum of a Set?
A8)
Let S be a set bounded above. The least of all the upper bounds of S is called the least upper bound or the Supremum of S. Thus, if a set S is bounded above, then a real number m is the supremum of S if the following two conditions are satisfied:
(i) m is an upper bound of S,
(ii) if k is another upper bound of S, then m 5 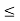 k.
k.
The greatest lower bound, in Latin terminology, is called the Infimum of a set.
Q9) Prove that the supremum of a set, if it exists, is unique.
A9)
If possible, let there be two supremums (Suprema) say m and m’ of a set $.
Since m is the least upper bound of S, therefore by definition, we have
m 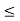 m’
m’
Similarly, since m’ the least upper bound of S, therefore, we must have
M’  m.
m.
This shows that m = m’ which proves the theorem.
Q10) What is called completeness property?
A10)
Every non-empty subset S of R which is bounded above, has the supremum.
Similarly, we have every non-empty subset S of R that is bounded below, has the infimum.
In fact, it can be easily shown that the above two statements are equivalent.
Now, if you consider a non-empty subset S of Q, then S considered as a subset of R must have, by property, a supremum. However, this supremum may not be in Q. This fact is expressed by saying that Q considered as a field in its down right is not Order-Complete.
Q11) State and prove Archimedean Property.
A11)
If x  R, then there exists
R, then there exists 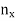
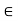 N such that x
N such that x 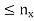
Proof:
If the assertion is false, then n 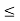 x for all n
x for all n 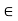 N; therefore, x is an upper bound of N. Therefore, by the Completeness Property, the nonempty set N has a supremum u
N; therefore, x is an upper bound of N. Therefore, by the Completeness Property, the nonempty set N has a supremum u 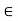 R. Subtracting 1 from u gives a number u - 1, which is smaller than the supremum u of N. Therefore u - 1 is not an upper bound of N, so there exists m
R. Subtracting 1 from u gives a number u - 1, which is smaller than the supremum u of N. Therefore u - 1 is not an upper bound of N, so there exists m 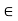 N with u - 1 < m. Adding 1 gives u < m + 1, and since m + 1
N with u - 1 < m. Adding 1 gives u < m + 1, and since m + 1  N, this inequality contradicts the fact that u is an upper bound of N.
N, this inequality contradicts the fact that u is an upper bound of N.
Q12) Prove that If S := {1/n : n 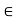 N}, then inf S = 0.
N}, then inf S = 0.
A12)
Since S 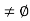 is bounded below by 0, it has an infimum and we let w := inf S. It is clear that w
is bounded below by 0, it has an infimum and we let w := inf S. It is clear that w  0. For any
0. For any 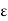 > 0, the Archimedean Property implies that there exists n
> 0, the Archimedean Property implies that there exists n 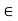 N such that 1/
N such that 1/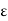 < n, which implies 1/n <
< n, which implies 1/n <  . Therefore we have
. Therefore we have
0  w
w 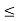 1/n <
1/n < 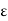 : But since
: But since 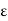 > 0 is arbitrary
> 0 is arbitrary
Q13) Prove that If t > 0, there exists 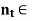 N such that 0 < 1/
N such that 0 < 1/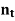 < t.
< t.
A13)
Since inf {1/n : n 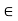 N} = 0 and t > 0, then t is not a lower bound for the set
N} = 0 and t > 0, then t is not a lower bound for the set
{1/n : n 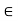 N}. Thus there exists
N}. Thus there exists 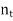
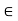 N such that 0 < 1/
N such that 0 < 1/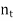 < t.
< t.
Q14) Prove that There exists a positive real number x such that 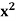 = 2.
= 2.
Q15)
Let S :{s 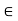 R : 0
R : 0 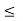 s;
s;  < 2}. Since 1
< 2}. Since 1 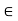 S, the set is not empty. Also, S is bounded above by 2, because if t > 2, then
S, the set is not empty. Also, S is bounded above by 2, because if t > 2, then 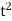 > 4 so that t does not belongs to S. Therefore the Supremum Property implies that the set S has a supremum in R, and we let x := sup S. Note that x > 1.
> 4 so that t does not belongs to S. Therefore the Supremum Property implies that the set S has a supremum in R, and we let x := sup S. Note that x > 1.
We will prove that 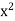 = 2 by ruling out the other two possibilities:
= 2 by ruling out the other two possibilities: 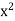 < 2 and
< 2 and 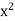 > 2.
> 2.
First assume that 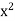 < 2. We will show that this assumption contradicts the fact that
< 2. We will show that this assumption contradicts the fact that
x = sup S by finding an n 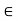 N such that x + 1/n
N such that x + 1/n  S, thus implying that x is not an upper bound for S. To see how to choose n, note that 1/
S, thus implying that x is not an upper bound for S. To see how to choose n, note that 1/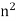
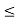 1/n so that
1/n so that

Hence if we can choose n so that
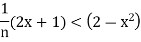
Then we get 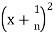 <
< 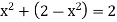 . By assumption we have 2 -
. By assumption we have 2 - 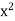 > 0, so that (2-
> 0, so that (2-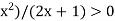 . Hence the Archimedean Property can be used to
. Hence the Archimedean Property can be used to
Obtain n 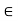 N such that
N such that
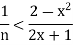
These steps can be reversed to show that for this choice of n we have x + 1=n 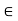 S, which contradicts the fact that x is an upper bound of S. Therefore we cannot have
S, which contradicts the fact that x is an upper bound of S. Therefore we cannot have  < 2.
< 2.
Now assume that 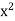 > 2.We will show that it is then possible to find m
> 2.We will show that it is then possible to find m 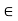 N such that
N such that
x - 1=m is also an upper bound of S, contradicting the fact that x = sup S. To do this, note that

Hence if we can choose m so that

Then 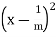 >
> >
>  – (
– (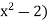 equals 2Now by assumption we have
equals 2Now by assumption we have  - 2 > 0, so that
- 2 > 0, so that 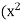 - 2)/2x > 0. Hence, by the Archimedean Property, there exists m
- 2)/2x > 0. Hence, by the Archimedean Property, there exists m 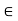 N such that
N such that
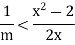
These steps can be reversed to show that for this choice of m we have 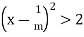
Now if s  S, then
S, then 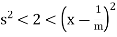 , whence it follows that s < x – 1/m. This implies that x - 1/m is an upper bound for S, which contradicts the
, whence it follows that s < x – 1/m. This implies that x - 1/m is an upper bound for S, which contradicts the
Fact that x = sup S. Therefore we cannot have 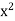 > 2. Since the possibilities
> 2. Since the possibilities 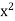 < 2 and
< 2 and  > 2 have been excluded, we must have
> 2 have been excluded, we must have 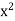 = 2. By slightly modifying the preceding argument, the reader can show that if a > 0, then there is a unique b > 0 such that
= 2. By slightly modifying the preceding argument, the reader can show that if a > 0, then there is a unique b > 0 such that 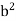 = a.We call b the positive square root of a and denote it by b =
= a.We call b the positive square root of a and denote it by b =  or b =
or b = 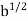 A slightly more complicated argument involving the binomial theorem can be formulated to establish the existence of a unique positive nth root of a.
A slightly more complicated argument involving the binomial theorem can be formulated to establish the existence of a unique positive nth root of a.
Q16) What do you understand by density of Rational Numbers in R
A15)
We now know that there exists at least one irrational real number,  .
.
Actually there are ‘‘more’’ irrational numbers than rational numbers in the sense that the set of rational numbers is countable, while the set of irrational numbers is
Uncountable.
However,we next show that in spite of this apparent disparity, the set of rational numbers is ‘‘dense’’ in R in the sense that given any two real numbers there is a rational number between them (in fact, there are infinitely many such rational numbers).
Q17) State density theorem.
A16)
If x and y are any real numbers with x < y, then there exists a rational number r 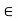 Q such that x < r < y.
Q such that x < r < y.
Note- If x and y are real numbers with x < y, then there exists an irrational number z such that x < z < y.
Q18) Explain intervals.
A17)
An interval in R is an non-empty subset of R which has the property that, whenever two numbers a and b belong to it, all numbers between a and b also belong to it.
Or in other words, A subset J 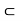 R is said to be an interval if a, b
R is said to be an interval if a, b 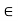 J and if
J and if
a < x < b, we then have x 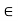 J:
J:
 a, b
a, b 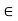 J and a < x < b =) x
J and a < x < b =) x 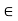 J
J
A real number x such that a < x < b is said to be between a and b.
The set N of natural numbers is not an interval because while 1 and 2 belong to N, but 1.5 which lies between 1 and 2, does not belong to N.
Let a, b 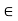 R with a
R with a 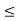 b.
b.
(i) Consider the set {x 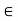 R : a
R : a 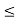 x
x 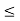 b}. This set is denoted by ]a, b[, and is called a closed interval. Note that the-end points a and b are included in it.
b}. This set is denoted by ]a, b[, and is called a closed interval. Note that the-end points a and b are included in it.
(ii) Consider the set{x 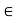 R : a < x < b}. This set is denoted by [a, b], and is called an open interval. In this case the end points a and b are not included in it,
R : a < x < b}. This set is denoted by [a, b], and is called an open interval. In this case the end points a and b are not included in it,
(iii) The interval {x 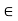 R: a
R: a 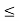 x < b} is denoted by [a, b[.
x < b} is denoted by [a, b[.
(iv) The interval {x  R : a < x
R : a < x 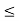 b} is denoted by ]a, b].
b} is denoted by ]a, b].
Example: Let a 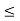 b be real numbers. We define
b be real numbers. We define
[a, b]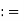 {x
{x 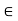 R: a
R: a 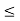 x
x 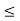 b}
b}
(a, b)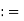 {x
{x  R: a < x < b}
R: a < x < b}
[a, b)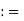 {x
{x  R: a
R: a  x < b}
x < b}
[a, b) {x
{x 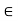 R: a < x
R: a < x 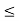 b}
b}
[a, ) {x
{x  R: x
R: x 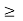 a}
a}
(a, ) {x
{x 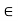 R: x > a}
R: x > a}
(-, b] {x
{x  R: x
R: x  b}
b}
(-, b)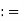 {x
{x 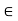 R: x < b}
R: x < b}
(-, )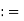 R
R
Intervals of these types are called bounded intervals. But remember that these are not finite sets. In fact these are infinite sets except for the case [a, a] = {a}.
Q19) Define open sets.
A18)
X a set S is said to be open if it is a neighbourhood of each of its points. Thus, a set S is open if for each x in S, there exists an open interval ]x – 6, x + 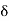 [,
[,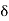 > 0 such that
> 0 such that
x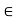 ] x –
] x – 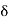 , x +
, x + 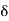 [
[  S.
S.
It follows at once that a set S is not open if it is not a neighbourhood of even one of its points.
Q20) Prove that an open interval is an open set.
A19)
Let ]a, b[ be an open interval. Then a < b. Let c] a, b[. Then a < c < b and therefore
c – a > 0 and b – c > 0
Choose
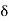 = Minimum of {b – c, c – a)
= Minimum of {b – c, c – a)
= Min (b – c, c – a).
Note that b – c > 0, c – a > 0. Therefore  > 0.
> 0.
Now 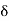
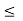 c – a
c – a 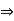 a
a  c –
c –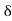
And 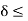 b – c
b – c  c +
c + 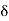 < b.
< b.
i.e.
Therefore,]c – 6, c + 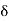 [
[ 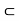 ]a, b[ and hence ]a, b[ is a neighbourhood of c.
]a, b[ and hence ]a, b[ is a neighbourhood of c.
Q21) Prove that a set is closed if and only if its complement is open.
A20)
We assume that S is a closed set. Then we prove that its complement Sc is open.
To show that 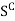 is open, we have to prove that
is open, we have to prove that 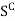 is a NBD of each of its points. Let x
is a NBD of each of its points. Let x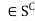 . Then, x
. Then, x  implies x
implies x 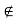 S. This means x is not a limit point of S because S is given to be a closed set. Therefore, there exists a
S. This means x is not a limit point of S because S is given to be a closed set. Therefore, there exists a 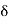 > 0 such that ]x –
> 0 such that ]x – 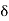 , x +
, x + 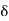 [ contains no points of S. This means that ]x –
[ contains no points of S. This means that ]x – 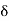 , x +
, x +  [ is contained in Sc. This further implies that Sc is a NBD of x. In other words,
[ is contained in Sc. This further implies that Sc is a NBD of x. In other words,  is an open set, which proves the assertion.
is an open set, which proves the assertion.
Conversely, let a set S be such that its complement 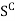 is open. Then we prove that S is closed. To show that S is closed, we have to prove that every limit point x of S belongs to S. Suppose x
is open. Then we prove that S is closed. To show that S is closed, we have to prove that every limit point x of S belongs to S. Suppose x 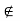 S, Then x
S, Then x  .
.
This implies that 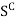 is a NBD of x because Sc is open. This means that there exists an open interval
is a NBD of x because Sc is open. This means that there exists an open interval
]x – 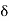 , x +
, x + 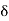 [, for some 6 > 0, such that
[, for some 6 > 0, such that
]x – 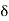 , x +
, x +  [
[
In other words, ]x – 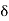 , x +
, x +  [ contains no point of S. Thus x is not a limit point of S, which is a contradiction. Thus our supposition is wrong and hence, x
[ contains no point of S. Thus x is not a limit point of S, which is a contradiction. Thus our supposition is wrong and hence, x 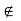 S is not possible. In other words, the (limit) point x belongs to S and thus S is a closed set.
S is not possible. In other words, the (limit) point x belongs to S and thus S is a closed set.
Q22) Prove that every infinite bounded set has a limit point.
A21)
Let S be a infinite bounded set and m, M its infimum and supremum respectively.
Suppose P is a set of real numbers defined as follows:
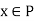 iff it exceeds at the most a finite number of members of S.
iff it exceeds at the most a finite number of members of S.
The set P is non-empty for 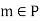 . Also M is an upper bound of P. For no number greater than or equal to M can belong to P. Thus the real number set P is non-empty and is bounded above.
. Also M is an upper bound of P. For no number greater than or equal to M can belong to P. Thus the real number set P is non-empty and is bounded above.
Therefore by the order-completeness property, P has a supremum say  .
.
We shall now show that 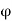 is a limit point of S.
is a limit point of S.
Consider any neighbourhood ]  where
where 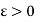
Since 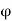 is the supremum of P, there exists at least one member say
is the supremum of P, there exists at least one member say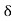 of P such that
of P such that 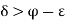 .
.
Now 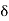 belongs to P, therefore it exceeds at the most a finite number of members of S, and consequently
belongs to P, therefore it exceeds at the most a finite number of members of S, and consequently 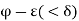 can exceed at the most a finite number of members of S.
can exceed at the most a finite number of members of S.
Again as 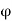 is the supremum of P,
is the supremum of P, 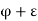 can not belong to P, and consequently
can not belong to P, and consequently 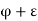 must exceed an infinite number of members of S.
must exceed an infinite number of members of S.
Now  exceeds at the most a finite number of members of S and
exceeds at the most a finite number of members of S and 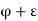 exceeds infinitely many members of S,
exceeds infinitely many members of S,
Implies that- [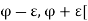 contains an infinite number of members of S.
contains an infinite number of members of S.
Consequently 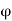 is a limit point of S.
is a limit point of S.
Q23) What do you understand by interior of a set?
A22)
Let (X,τ)be the topological space and A⊆X, then a point x∈A is said to be an interior point of set A, if there exists an open set U such that
x∈U⊆A
In other words let A be a subset of a topological space X, a point x∈A is said to be an interior points of A if x is in some open set contained in A.