Unit - 1

Partial Differential Equations

Q1) What do you understand by differential equations?

A1)

An equation containing the derivatives or differentials of one or more dependent variables with respect to one or more independent variables is called a differential equation.

Example:

Notation: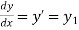

………………..

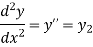
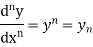
Order of a differential equation:

The order of the highest derivative involved in the differential equation i.e. how many times it is differentiated is called the order of the differential equation.

Degree of the differential equation:

The degree of the highest derivative involved in the differential equation after made free from radicals and fractions as far as derivatives are concerned i.e.  power of the highest derivative is called the degree of the differential equation.

Q2) How do we form differential equations?

A2)

To construct the differential equation from the given family of curve in x and y containing n arbitrary constants.

1. Write the given family of curves.
2. Differentiate n times to get n equations.
3. Eliminate the n arbitrary constant using (a) and (b).

Q3) Form the differential equation of ?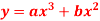

A3)

Given curve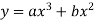

Differentiating the above curve with respect to x.

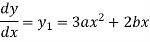
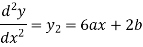
Multiplying both side by x.

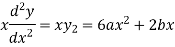
Now, 

                                          =0

Hence the required equation is

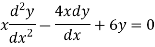
Q4) Define PDE.

A4)

A partial differential equation (PDE) is an equation involving one or more partial derivatives of an (unknown) function, call it u, that depends on two or more variables, often time t and one or several variables in space. The order of the highest derivative is called the order of the PDE. Just as was the case for ODEs, second-order PDEs will be the most important ones in applications.

A partial differential equation is one in which y depends on two or more independent variables say x, t, . . . (so that the derivatives of y are partial derivatives.)

Just as for ordinary differential equations (ODEs) we say that a PDE is linear if it is of the first degree in the unknown function u and its partial derivatives. Otherwise we call it nonlinear.

The standard methods of solving the differential equations of the following

Types:

(i)                Equations solvable by separation of the variables.

(ii)              Homogeneous equations.

(iii)           Linear equations of the first order.

(iv)            Exact differential equations.

Q5) What is quasi-linear & semi-linear equation?

A5)

A PDE is said to be quasi-linear if the derivatives of the highest order which occur in the equation are linear.

A quasi-linear PDE is called semi-linear if the coefficients of the highest order derivatives do not contain either the dependent variable or its derivative.

A semi-linear PDE is called linear if it is linear in the dependent variable and its derivative.

Q6) What are first order PDE and how do we format them?

A6)

Classification of first order partial differential equations-

1. A first order PDE is called linear equation if it is linear in p, q and z.

It is written as-

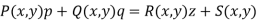
2.     A first order PDE is called semi-linear equation if it is linear in p and q are functions of x and y only if it is of the form

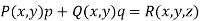
3.     A first order PDE is called quasi-linear equation if it is linear in p and q. It is of the form

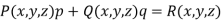
Formation of PDE-

Let

f (x, y, z, a, b) = 0  …… (1)

Be an equation involving two arbitrary constants a and b. Differentiating this equation partially with respect to x and y, we get

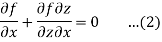
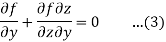
By eliminating a, b from (1), (2), (3), we get an equation of the form

F (x, y, z, p, q) = 0 …………..(4)

Which is a partial differential equation of first order.

Q7) Form a partial differential equation from-

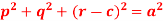
A7)

Here we have-

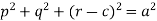
It contains two arbitrary constants a and c

Differentiate the equation with respect to p, we get-

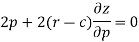
Or

Now differentiate the equation with respect to q, we get-

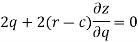
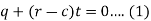
Now eliminate ‘c’,

We get

Now put z-c in (1), we get-

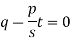
Or

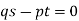
Q8) Find the differential equation of all spheres whose centres lie on the z-axis.

A8)

The equation is - , here a and b are the constants.

Now on differentiating, we get

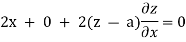
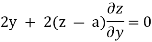
From the second equation

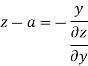
Now put this value in equation first, we get

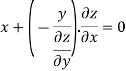
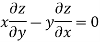
Q9) Solve-

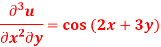
A9)

Here we have-

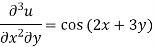
Integrate w.r.t. x, we get-

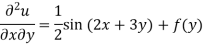
Integrate w.r.t. x, we get-

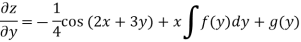
Integrate w.r.t. y, we get-

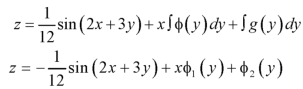
Q10) Solve the differential equation-

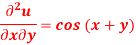
Given that 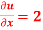when y = 0, and u = 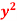when x = 0.

A10)

We have-

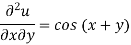
Integrating partially w.r.t. y, we get-

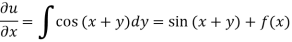
Now from the boundary conditions,

Then-

From which,

It means,

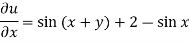
On integrating partially w.r.t. x givens-

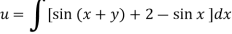
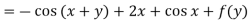
From the boundary conditions, u = when x = 0

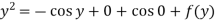
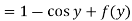
From which-

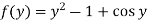
Therefore the solution of the given equation is-

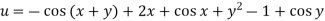
Q11) Solve   

A11)

Rewriting the given equation as

The subsidiary equations are

The first two fractions give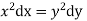

Integrating we get 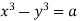   n    (i)

Again the first and third fraction give xdx = zdz

Integrating, we get

Hence from (i) and (ii), the complete solution is

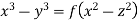
Q12) Solve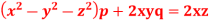

A12)

Here the subsidiary equations are

From the last two fractions, we have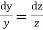

Which on integration gives log y = log z + log a or y/z=a     (i)

Using multipliers x, y and z we have

Each fraction

Which on integration gives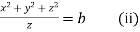

Hence from (i) and (ii) the required solution is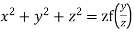

Q13) Solve-

A13)

Let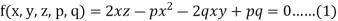
 

Charpit’s subsidiary equations are-

So that- dq = 0 or q = a

On putting q = a in (1) we get-

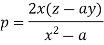
Such that-

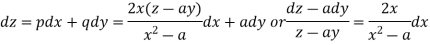
Integrating

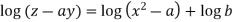
Or

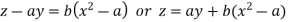
Which is the required solution

Q14) Solve-

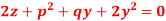
A14)

Let

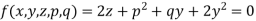
Charpit’s subsidiary equations are-

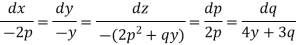
From the first and fourth ratios,

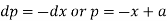
Substituting p = a – x in the given equation, we get-

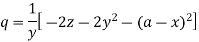
So that-

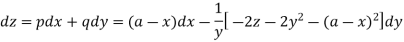
Multiply both sides by ,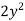

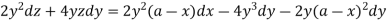
Integrating-

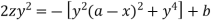
Or

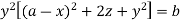
Which is the required solution.

Q15) Solve the following-

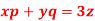
A15)

This is a linear P.D.E. Of first order Pp + Qq = R with P = x, Q = y and R = 3z. The Lagrange’s auxiliary equations are

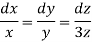
Integrating the first two equations , we obtain

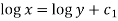
Integrating first and the last equations, we obtain

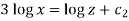
Hence

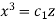
Thus the required solution is

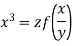
Q16) Solve-

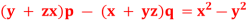
A16)

Auxiliary equations-

Choosing multipliers as x, y, −z

Xd x + ydy − zd z = x(y + zx) + y(−1)(x + yz) – z (

Integrating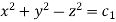

Choosing multipliers as y, x, 1, we get

Yd x + xdy + d z = y(y + zx) + x(−1)(x + yz) +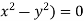

Integrating xy + z = c2

The general solution is

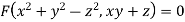
Q17) Solve-

A17)

Auxiliary equations are

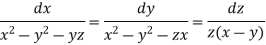
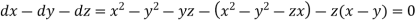
On integrating

x − y − z = c1

From first and second, we get

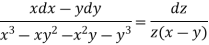
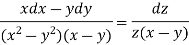
Which means

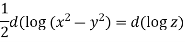
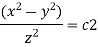
The general solution will be

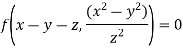
Q18) Using the method of separation of variables, solve Where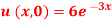

A18)

Assume the given solution

Substituting in the given equation, we have

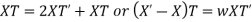
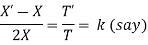
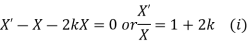
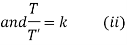
Solving (i)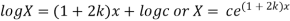

From (ii)

Thus

Now,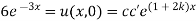

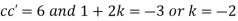
Substituting these values in (iii) we get

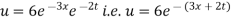
Which is the required solution.