Unit - 3
Improper integrals
Q1) Define definite integrals.
A1)
When we apply limits in indefinite integrals are called definite integrals.
If an expression is written as 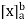 , here ‘b’ is called upper limit and ‘a’ is called lower limit.
, here ‘b’ is called upper limit and ‘a’ is called lower limit.
If f is an increasing or decreasing function on interval [a , b], then
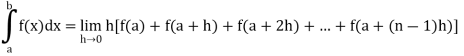
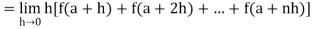
Where 
Q2) Evaluate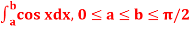 .
.
A2)
Here we notice that f:x→cos x is a decreasing function on [a , b],
Therefore by the definition of the definite integrals-
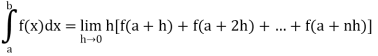
Then
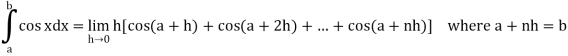
Now,
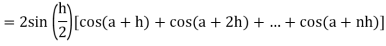
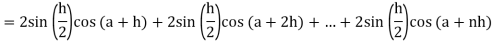
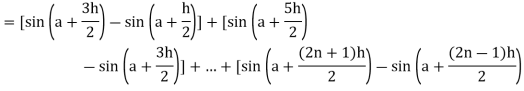

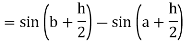
Here 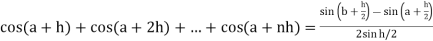
Thus
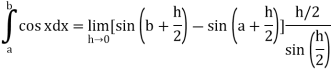
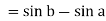
Q3) Evaluate 
A3)
Here  is an increasing function on [1, 2]
is an increasing function on [1, 2]
So that,
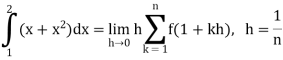
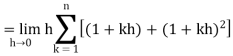
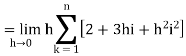
 …. (1)
…. (1)
We know that-
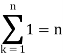
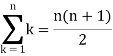
And

Then equation (1) becomes-

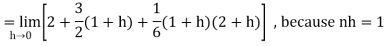
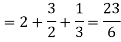
Q4) Evaluate-
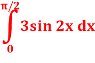 A4)
A4)
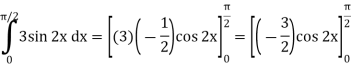
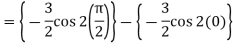

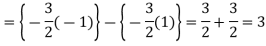
Q5) Explain improper integrals over finite intervals.
A5)
- Let f is function defined on (a, b] and
 exists for all t ∈(a, b) , then
exists for all t ∈(a, b) , then
If  exists, then we define the improper integral of f over (a, b] as follows-
exists, then we define the improper integral of f over (a, b] as follows-
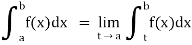
(2) Let f is function defined on [a, b) and 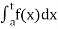 exists for all t ∈(a,b) , then
exists for all t ∈(a,b) , then
If  exists, then we define the improper integral of f over [a, b) as follows-
exists, then we define the improper integral of f over [a, b) as follows-
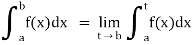
(3) Let f is function defined on [a, c) and (c, b]. If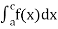 and
and 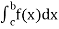 exist then we define the improper integral of f over [a, b] as follows-
exist then we define the improper integral of f over [a, b] as follows-

Q6) What do you understand by convergence at left end?
A6)
Let a be the only points of infinite discontinuity of f so that according to assumption made in the last section, the integral
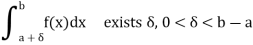
𝑇ℎ𝑒 𝑖𝑚𝑝𝑟𝑜𝑝𝑒𝑟 𝑖𝑛𝑡𝑒𝑔𝑟𝑎𝑙  is defined as the
is defined as the
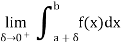
So that

If this Limit exists and is finite, the improper integral 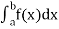 is said to converge at (a) if otherwise, it is called divergent.
is said to converge at (a) if otherwise, it is called divergent.
Q7) What do you understand by convergent at right-end?
A7)
Suppose b be the only point of infinite discontinuity the improper integral is then defined by the relation
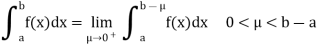
If the limit exists, the improper integral is said to be convergent at 𝑏. Otherwise
Is called divergent.
Q8) What is the comparison test in limit form?
A8)
If f and g are two positive functions [a, b] and ‘a’ is the only singular point of f and g in [a, b], such that
𝑙𝑖𝑚𝑥→𝑎+(𝑥)𝑔(𝑥) = l
Where ‘l’ is a non – zero finite number.
Then, the two integrals 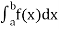 and
and  converges and diverges
converges and diverges
Together at ‘a’.
Q9) Test the convergence of
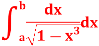
A9)
Here we have
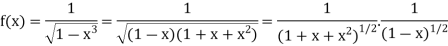
Here we can see that 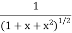 is a bounded function.
is a bounded function.
Suppose M is its upper bound then
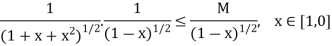
Also since
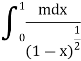
Is convergent as n = ½ < 1. Therefore,
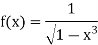
Is convergent.
Q10) Show that  is divergent.
is divergent.
A10)
Let us suppose

Here x=1 is only singular point.
Take (𝑥) =1/x-1
Then
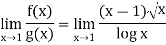
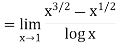
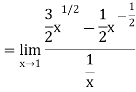
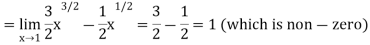
Thus, 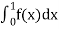 and
and  are same.
are same.
Since 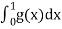 is divergent, hence
is divergent, hence  is divergent.
is divergent.
Q11) What is the convergence of beta function?
A11)
It is a proper integral for 𝑚≥1, ≥1 , 0 and 1 are the only points of infinite discontinuity; 0 when m < 1 and 1. When n < 1, we have
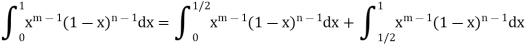
Converges at 0, when m < 1,
Suppose
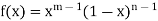

Take g(x) = 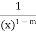
Then

Since 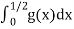 converges iff. 1 – m < 1 or m > 0.
converges iff. 1 – m < 1 or m > 0.
Thus
 converges for m > 0.
converges for m > 0.
Converges at x = 1,
We take

Take
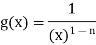
Then
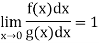
Also 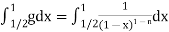 converges if and only if 1−n < 1 or n > 0.
converges if and only if 1−n < 1 or n > 0.
Thus, 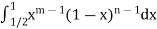 converges if n > 0.
converges if n > 0.
Hence 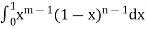 converges if m > 0, n > 0.
converges if m > 0, n > 0.
Q12) Show that 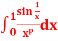 , p>0 converges absolutely for p<1.
, p>0 converges absolutely for p<1.
A12)
Suppose
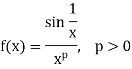
‘0’ is the only point of infinite discontinuity and f does not keeps the same sign in [0, 1].
So that
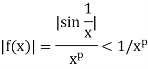
Also 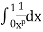 converges for 𝑝 < 1
converges for 𝑝 < 1
Thus
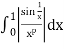 converges if and only if p > 0.
converges if and only if p > 0.
Hence
 is absolutely convergent if and only if 𝑝 < 1 .
is absolutely convergent if and only if 𝑝 < 1 .
Q13) What is the convergence at infinity?
A13)
The symbol 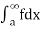 , 𝑥≥ 𝑎 is defined as limit of
, 𝑥≥ 𝑎 is defined as limit of 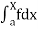 when x tends to infinity, so that
when x tends to infinity, so that
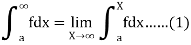
If the limit exists and is finite then the improper integral (1) is said to be divergent.
Q14) Show that 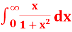 is divergent.
is divergent.
A14)
For X > 0, we have
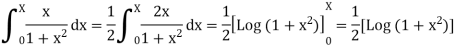
Here
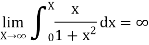
So that 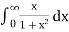 is divergent.
is divergent.
Q15) What do you understand by the convergence of gamma function?
A15)
Suppose
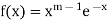
If 𝑚 < 1, the ‘0’ infinite discontinuity.
So we need to examine the convergence of above improper integral at both 0 and ∞.
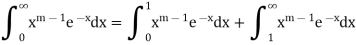
Convergence at 0 for 𝒎<1:
Let

Then

Since 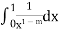 converges, if and only if m>0.
converges, if and only if m>0.
Therefore  converges if and only if 𝑚>0
converges if and only if 𝑚>0
Convergence at 
Let
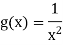
So that
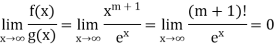
Since  is divergent
is divergent
Thus  is convergent for every m.
is convergent for every m.
Hence 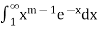 is convergent if and only if 𝑚> 0 and is denoted by < 𝑚) .
is convergent if and only if 𝑚> 0 and is denoted by < 𝑚) .
Thus
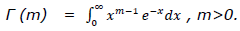
Thus Γ(0), Γ(-1), etc. are not exists .
Q16) Define sequence and series of a function.
A16)
Let  be a real valued function defined on an interval I and for each
be a real valued function defined on an interval I and for each  , then <
, then < is called a sequence of real valued function on I.
is called a sequence of real valued function on I.
We denote it by { } or <
} or < >
>
If 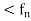 > is a sequence of real valued function on an interval I, then
> is a sequence of real valued function on an interval I, then 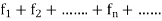 is called the series of real valued function defined on an interval I.
is called the series of real valued function defined on an interval I.
This series is denoted by 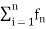
That is, we shall consider sequences whose terms are functions rather than real numbers. These sequences are useful in obtaining approximations to a given function.
Q17) Explain point-wise convergence.
A17)
Let 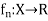 be a sequence of functions from a set X to R.
be a sequence of functions from a set X to R.
We say that 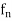 converges to f pointwise on X if for each
converges to f pointwise on X if for each  the sequence (
the sequence ( of real numbers converges to the real number f(x) in R.
of real numbers converges to the real number f(x) in R.
Like we say a sequence (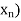 is convergent on X. We may also define a sequence of function (
is convergent on X. We may also define a sequence of function ( is pointwise convergent on X.
is pointwise convergent on X.
This means that there exists a function  such that (
such that (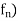 is pointwise convergent to f. There is another problem for us. We need to find the limit function f and then show that
is pointwise convergent to f. There is another problem for us. We need to find the limit function f and then show that  pointwise.
pointwise.
This means that we fix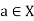 first and form the sequence
first and form the sequence 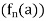 of real numbers.
of real numbers.
For any given 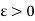 , we have to find an
, we have to find an  such that
such that 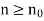 we have |
we have |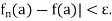
Thus  may depend not only on
may depend not only on 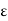 but also on a.
but also on a.
Q18) Prove that A sequence of differentiable functions { 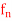 } with limit 0 for which {
} with limit 0 for which {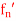 } diverges
} diverges
A18)
Let
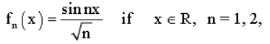
Then

But
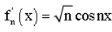
And so

Q19) What is uniform convergence?
A19)
A sequence of function { is said to converge uniformly to a function f on a set E if for every
is said to converge uniformly to a function f on a set E if for every  there exists and integer N such that n > N implies
there exists and integer N such that n > N implies

If each tern of the sequence <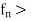 is real-valued, then the expression (1) can be written as
is real-valued, then the expression (1) can be written as

Definition: A series 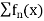 is said to be uniformly convergent on E if the sequence
is said to be uniformly convergent on E if the sequence  of partial sums defined by
of partial sums defined by  converges uniformly on E.
converges uniformly on E.
Q20) Let  be a sequence of continuous functions on a set E
be a sequence of continuous functions on a set E  R and suppose that
R and suppose that  converges uniformly on E to a function f: E
converges uniformly on E to a function f: E  R . Then the limit function f is continuous.
R . Then the limit function f is continuous.
A20)
Suppose c E be an arbitrary point. If c is an isolated point of E, then f is automatically continuous at c. So suppose that c is an accumulation point of E. We shall show that f is continuous at c. Since
E be an arbitrary point. If c is an isolated point of E, then f is automatically continuous at c. So suppose that c is an accumulation point of E. We shall show that f is continuous at c. Since  uniformly, for every
uniformly, for every  > 0 there is an integer N such that n
> 0 there is an integer N such that n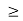 N implies
N implies
| (x) –f(x)| <
(x) –f(x)| <  for all x
for all x  E
E
Since  is continuous at c, there is a neighbourhood
is continuous at c, there is a neighbourhood  such that x
such that x 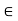
 (since c is limit point) implies
(since c is limit point) implies
|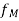 (x) –
(x) – (c)| <
(c)| < 
By triangle inequality, we get
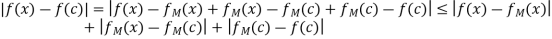
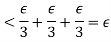
Hence
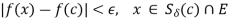
Which is the proof of continuity of f at arbitrary point 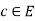 .
.