Unit - 1
Rate of convergence
Q1) Define order of convergence.
A1)
Let 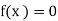 be the given equation. Let α be its exact root.
be the given equation. Let α be its exact root.
Then 
Then the positive number p is said to be order of convergence if,

If p=1, then convergence is linear and if p=2, then it is quadratic.
An iterative method is said to be kth order convergent if k is the largest positive real
Number such that

Here A is a non-zero finite number called asymptotic error constant and it depends on derivative of f(x) at an approximate root x.
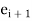 and
and 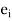 are the errors in successive approximation.
are the errors in successive approximation.
Q2) What is an absolute and relative error?
A2)
Absolute Error:
The Approximate error is the numerical difference between the quantity of exact solution and the approximate value of the solution.
Let X be the exact solution and the approximate value of the solution is denoted by  , then the absolute error is defined as
, then the absolute error is defined as

Relative Error:
The error obtained by dividing the approximate solution to the exact solution is known as relative error and is denoted by 
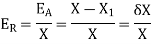
The percentage error is the 100 times of the relative error i.e.
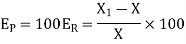
The absolute accuracy is magnitude absolute error.
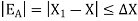
The relative accuracy is the magnitude of the relative error.
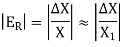
Q3) An approximate value of  is given by
is given by  and its exact value is
and its exact value is 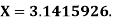 Find the absolute and relative errors.
Find the absolute and relative errors.
A3)
The absolute error is 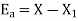
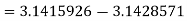
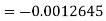 .
.
The relative error is

Q4) Find the difference 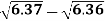 to three significant figure?
to three significant figure?
A4)

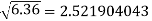
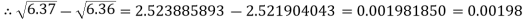
Correct to three decimal places.
Q5) Find the absolute error if the number 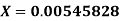 is truncate to three decimal places?
is truncate to three decimal places?
A5)
The given number is 
After truncate it to three decimal places the rounded value is 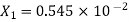
Therefore the absolute error is 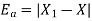
= 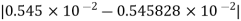
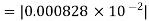
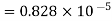 .
.
Q6) Explain generalized error formula.
A6)
Let-

Be the function of 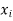 and let the error in each
and let the error in each  be
be 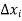 .
.
The error in u is given by-
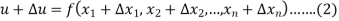
By using Taylor’s theorem we expand RHS-
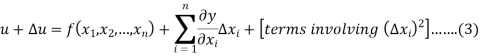
Lets assume that the errors in 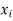 are small, so that the higher powers of
are small, so that the higher powers of 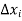 can be neglected,
can be neglected,
The above relation yields-
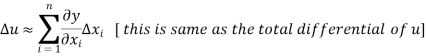
The formula for the relative error follows-
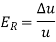
Q7) Find the real root of the equation
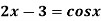
A7)
Correct to three decimal places in the interval  ]
]
The given equation is 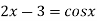 ..(1)
..(1)
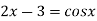
Or 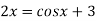
Or 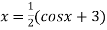 =
= 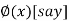 ..(2)
..(2)
Or 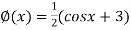
Let 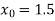 , in the interval
, in the interval 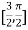 .
.
The successive approximation we have
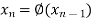
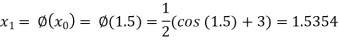
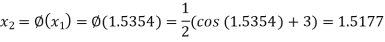
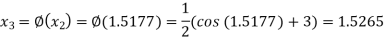
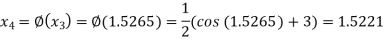
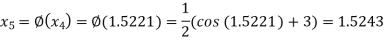
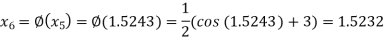
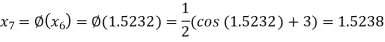
Hence the root of the equation correct to three decimal places is 1.524.
Q8) Find the real root of the polynomial  correct to three decimal places?
correct to three decimal places?
A8)
Given equation 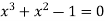 ….(1)
….(1)
Here 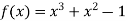
Also 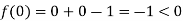

Therefore root of the equation lies between 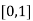 .
.
Again 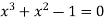
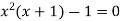

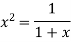
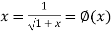 ….(2)
….(2)
Let 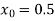 , in the interval
, in the interval 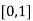 .
.
The successive approximation we have
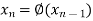
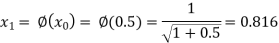
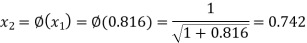

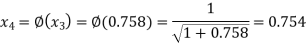
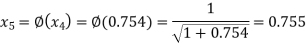
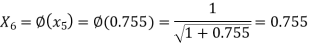
Hence the root of the equation correct to three decimal places is 0.755.
Q9) What do you understand by stable and unstable methods?
A9)
In an initial value problems, we need the solution for  and usually up to a point x = b.
and usually up to a point x = b.
The length of step h for application of any numerical method for the initial value problem should be chosen properly.
There are only two types of errors in computation- truncation and round off error.
We can handle the truncation error but round-off error can be handled, i.e. this is not in the hands of user. They can increase and can destroy the solution too.
Then we say that the method is numerically unstable.
When the step length is chosen larger than the allowed limiting value, in this case we come across with this situation.
Many explicit methods have no restrictions on the step length can be used.
These methods are called unconditionally stable method.
Q10) Write a note on arithmetic mathematical software.
A10)
Mathematical software is used to mode, calculate, analyze or visualize the numeric or geometric dataset.
There are various categories of mathematical software for different task relate to mathematical data.
A calculator, which is also a software allows the user to perform simple mathematical calculations such as, addition, subtraction, trigonometry, geometry, exponential, etc. we get the output in text format after entering the data manually.
To solve the algebraic equations, there are various computer algebraic systems. They are especially designed to solve the algebraic equations, and give the accurate solutions.
A lot of computer tools are available to analyze, visualize the statistical data sets, such as R programming, SAS, MS- excel. SPSS, stata, statistica, Julia, dataplot etc.
MATLAB is widely used software for numerical computations. It has its own programming language. We can implement the numerical algorithms.
GNU octave is the high-level language, generally made for numerical computations.
We can solve linear and non-linear problems numerically by using it.
- FFTW is a collection of fast C routines for computing the discrete Fourier transform in one or more than one dimensions. It has complex, real and parallel transforms and can handle arbitrary array sizes efficiently.
- LAPACK is a standard library for numerical linear algebra.
- SuperLU is a library which perform an LU decomposition for the direct solution of large and non-symmetric system of linear equations on high performance machines. It is written in C.
Q11) Find a real root of 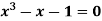 using bisection method correct to five decimal places.
using bisection method correct to five decimal places.
A11) Let 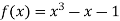 then by hit and trial we have
then by hit and trial we have

Thus 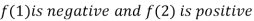 .So the root of the given equation should lies between 1 and 2.
.So the root of the given equation should lies between 1 and 2.
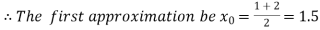
Now, 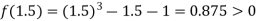
i.e. positive so the root of the given equation must lies between 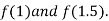

Now, 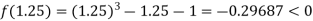
i.e. negative so the root of the given equation lies between 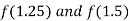
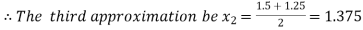
Now, 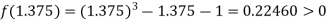
i.e. positive so the root of the given equation lies between 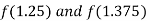
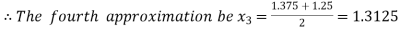
Now, 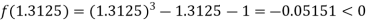
i.e. negative so that the root of the given equation lies between 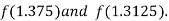
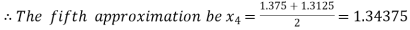
Now, 
i.e. positive so that the root of the given equation lies between 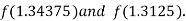
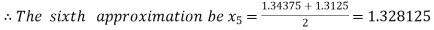
Now, 
i.e. positive so that the root of the given equation lies between 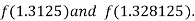
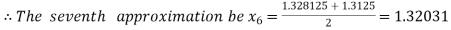
Now, 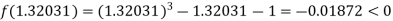
I.e. negative so that the root of the given equation lies between 

Now, 
i.e. negative so that the root of the given equation lies between 
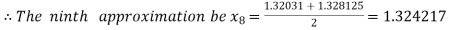
Hence the approximate root of the given equation is 1.32421
Q12) Find the root of the equation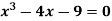 , using the bisection method.
, using the bisection method.
A12)
Let 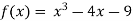 then by hit and trial we have
then by hit and trial we have

Thus  .So the root of the given equation should lies between 2 and 3.
.So the root of the given equation should lies between 2 and 3.
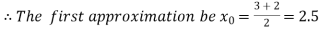
Now, 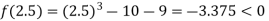
i.e. negative so the root of the given equation must lies between 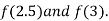
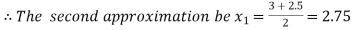
Now, 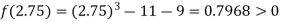
i.e. positive so the root of the given equation must lies between 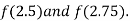
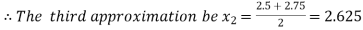
Now, 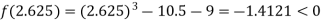
i.e. negative so the root of the given equation must lies between 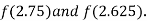
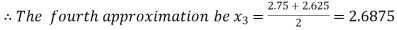
Now, 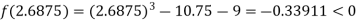
i.e. negative so the root of the given equation must lies between 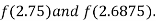
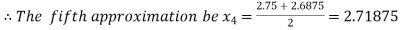
Now, 
i.e. positive so the root of the given equation must lies between 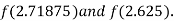
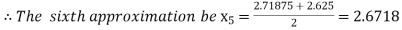
Now, 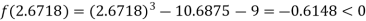
i.e. negative so the root of the given equation must lies between 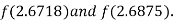

Hence the root of the given equation correct to two decimal place is 2.67965.
Q13) Find a real root of the equation  near
near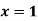 , correct to three decimal place by the Regula Falsi method.
, correct to three decimal place by the Regula Falsi method.
A13)
Let 
Now, 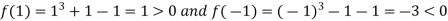
And also 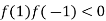
Hence the root of the equation 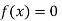 lies between
lies between 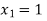 and
and 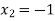 and so,
and so, 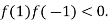
By Regula Falsi Method

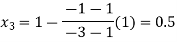
Now, 
So the root of the equation 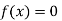 lies between 1 and 0.5 and so
lies between 1 and 0.5 and so 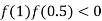
By Regula Falsi Method
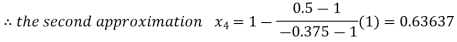
Now, 
So the root of the equation 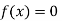 lies between 1 and 0.63637 and so
lies between 1 and 0.63637 and so 
By Regula Falsi Method
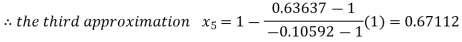
Now, 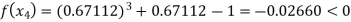
So the root of the equation  lies between 1 and 0.67112 and so
lies between 1 and 0.67112 and so 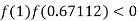
By Regula Falsi Method
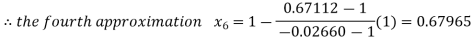
Now, 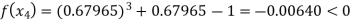
So the root of the equation  lies between 1 and 0.63636 and so
lies between 1 and 0.63636 and so 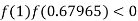
By Regula Falsi Method
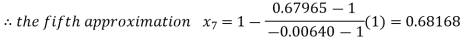
Now, 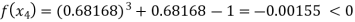
So the root of the equation 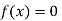 lies between 1 and 0.68168 and so
lies between 1 and 0.68168 and so 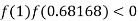
By Regula Falsi Method
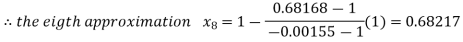
Now, 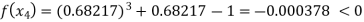
Hence the approximate root of the given equation near to 1 is 0.68217
Q14) Find the real root of the equation
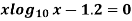
A14)
By the method of false position correct to four decimal places
Let 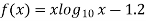
By hit and trail method
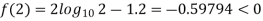
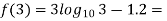 0.23136 > 0
0.23136 > 0
So, the root of the equation 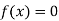 lies between
lies between  2 and
2 and 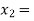 3 and also
3 and also 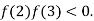
By Regula Falsi Method
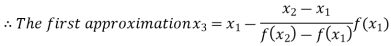

Now, 
So, root of the equation 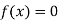 lies between 2.72101 and 3 and also
lies between 2.72101 and 3 and also 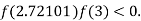
By Regula Falsi Method

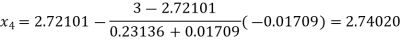
Now, 
So, root of the equation  lies between 2.74020 and 3 and also
lies between 2.74020 and 3 and also 
By Regula Falsi Method
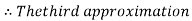

Now, 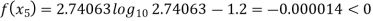
So, root of the equation 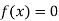 lies between 2.74063 and 3 and also
lies between 2.74063 and 3 and also 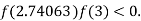
By Regula Falsi Method
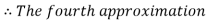

Hence the root of the given equation correct to four decimal places is 2.7406
Q15) Using the Secant Method find the root of the equation correct to three decimal places
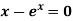
A15)
Let 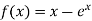
By Secant Method
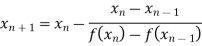
Let the initial approximation be
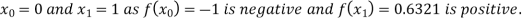
For n=1, the first approximation 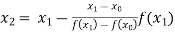
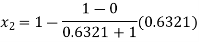
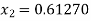
Now, 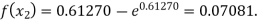
For n=2, the second approximation 
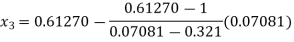
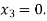 563839
563839
Now, 
For n=3, the third approximation 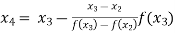

 56717
56717
Now, 
For n=4, the fourth approximation 
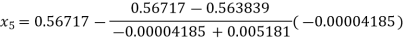
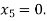 567143
567143
Hence the root of the given equation correct to four decimal places is 0.5671.
Q16) Using Secant Method find the root of the equation correct to four decimal place
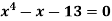
A16)
Let 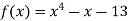
By Secant Method
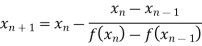
Let the initial approximation be
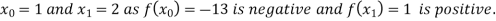
For n=1, the first approximation 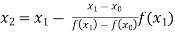


Now, 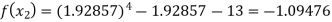
So the root of the equation lies between 2 and 1.92857
For n=2, the second approximation ,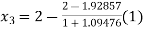
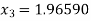
Now, 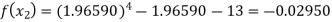
So the root of the equation lies between 2 and 1.96590
For n=3, the third approximation
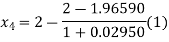
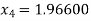
Now, 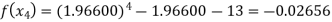
So the root of the equation lies between 2 and 1.96600
For n=4, the fourth approximation

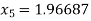
Now, 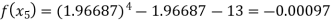
So the root of the equation lies between 2 and 1.96687
For n=5, the fifth approximation
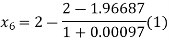
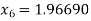
Now, 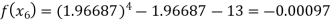
So the root of the equation lies between 2 and 1.96690
For n=6, the sixth approximation
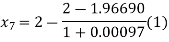
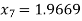
Now, 
Hence the root of the given equation correct to four decimal places is 1.9669.
Q17) Using Newton-Raphson method, find a root of the following equation correct to 3 decimal places: 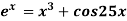 near to 4.5
near to 4.5
A17)
Let 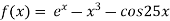
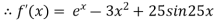
The initial approximation 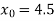
By Newton Raphson Method
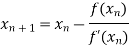
For n =0, the first approximation 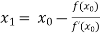
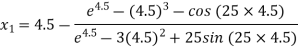

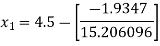
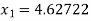
For n =1, the second approximation 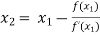
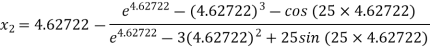

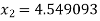
For n =2, the third approximation 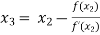

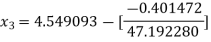
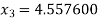
For n =3, the fourth approximation 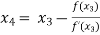

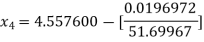
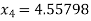
Hence the root of the equation correct to three decimal places is 4.5579
Q18) Using Newton-Raphson method, find a root of the following equation correct to 4 decimal places: 
A18)
Let 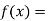
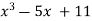

By Newton Raphson Method
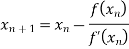


Let the initial approximation be 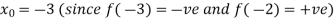
For n=0, the first approximation 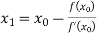
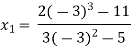

For n=1, the second approximation 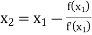
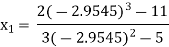

For n=2, the third approximation 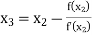

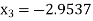
Since 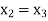 therefore the root of the given equation correct to four decimal places is -2.9537
therefore the root of the given equation correct to four decimal places is -2.9537
Q19) Explain fixed point iteration formula.
A19)
Fixed point iteration method is also called general iteration method.
In the very first step in this method, we write the equation f(x) = 0 in an equivalent form such as-
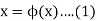
Now we find a root of f(x) = 0 is same as finding a number 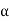 such that
such that  that is a fixed point of
that is a fixed point of  .
.
Using equation (1), the iteration method can be written as-
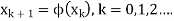
The function  is known as the iteration function.
is known as the iteration function.
We compute the next approximation as, (starting with the initial approximation)-
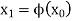


...........
...........
...............
................
Q20) Find the smallest positive root of the equation  by using fixed point iteration method.
by using fixed point iteration method.
A20)
Here we have-
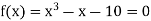
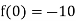

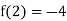
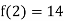
Since f(2) f(2) < 0, the smallest positive root lies in the interval (2, 3).
Now write-
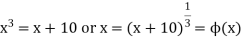
We define the iteration method as-
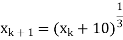
We get-

We find | < 1 for all x in interval (2, 3), hence the iteration converges
< 1 for all x in interval (2, 3), hence the iteration converges
Let
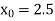 , we get the following results-
, we get the following results-
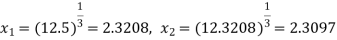

Since
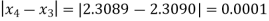
We take the required root as
x = 2.3089