Unit - 4

Divisibility in integral domains

Q1) Explain the Euclidean domain with examples?

A1)

A Euclidean domain (or Euclidean ring) is a ring that can be solved using the Euclidean algorithm.

In formal terms, a ring is a Euclidean domain if:

• It is an integral domain.
• There a function 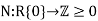 called a Norm such that for all nonzero  there are such that  and eithe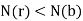r  or .
• Some common examples of Euclidean domains are:
• The ring of integers  with norm given by .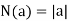
• The ring of Gaussian integers 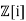 with norm given by .

Examples

Examples of Euclidean domains include:

• Any field. Define f (x) = 1 for all nonzero x.
• Z, the ring of integers. Define f (n) = |n|, the absolute value of n.[3]
• Z[ i ], the ring of Gaussian integers. Define f (a + bi) = a2 + b2, the norm of the Gaussian integer a + bi.
• Z[ω] (where ω is a primitive (non-real) cube root of unity), the ring of Eisenstein integers. Define f (a + bω) = a2 − ab + b2, the norm of the Eisenstein integer a + bω.

Q2) Explain the Irreducible?

A2)

An element  of a ring which is nonzero, not a unit, and whose only divisors are the trivial ones (i.e., the units and the products , where  is a unit). Equivalently, an element  is irreducible if the only possible decompositions of   into the product of two factors are of the form

Where 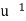 is the multiplicative inverse of .

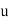Irreducible elements include prime numbers and irreducible polynomials, for example. The irreducible elements are the generators of the nonzero prime ideals in a principal ideal domain, hence they are exactly the prime elements. However, the two concepts are not interchangeable in general.

Q3) What are prime number? Explain its importance?

A3)

A prime number (or prime integer, often simply called a "prime" for short) is a positive integer  that has no positive integer divisors other than 1 and  itself. More concisely, a prime number  is a positive integer having exactly one positive divisor other than 1, meaning it is a number that cannot be factored. For example, the only divisors of 13 are 1 and 13, making 13 a prime number, while the number 24 has divisors 1, 2, 3, 4, 6, 8, 12, and 24 (corresponding to the factorization ), making 24 not a prime number. Positive integers other than 1 which are not prime are called composite numbers.

• Prime numbers are utilised in a variety of computer programmes, including public-key cryptography, which relies on the difficulty of factoring huge integers into prime factors.

• Prime elements and prime ideals are objects that behave like prime numbers in a generalised fashion.

• Primes are extremely essential to number theorists because they are the fundamental building blocks of whole numbers, and they are also extremely significant to the rest of the world since their peculiar mathematical features make them ideal for our contemporary applications.

Q4) Explain the Unique factorization domains?

A4)

A UFD is a nontrivial commutative ring in which the product of any two non-zero elements are non-zero. Every non-zero non-unit element can be expressed as a product of prime elements (or irreducible elements), uniquely up to order and units.

Integers and polynomial rings in one or more variables with coefficients derived from integers or fields are good examples of UFDs.

Formally, a unique factorization domain is defined to be an integral domain R in which every non-zero element x of R can be written as a product (an empty product if x is a unit) of irreducible elements pi of R and a unit u:

x = u p1 p2 ⋅⋅⋅ pn with n ≥ 0

And this representation is unique in the following sense: If q1, ..., qm are irreducible elements of R and w is a unit such that

x = w q1 q2 ⋅⋅⋅ qm with m ≥ 0,

Then m = n, and there exists a bijective map φ : {1, ..., n} → {1, ..., m} such that pi is associated to qφ(i) for i ∈ {1, ..., n}.

Because the uniqueness portion is often difficult to verify, the following equivalent definition is useful:

Every non-zero element of an integral domain R can be expressed as a product of a unit and prime elements of R.

Q5) Enlist the properties of UFD?

A5)

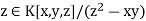
• In UFDs, every irreducible element is prime. (In any integral domain, every prime element is irreducible, but the converse does not always hold. For instance, the element {\displaystyle z\in K[x,y,z]/(z^{2}-xy)} is irreducible, but not prime.) Note that this has a converse: a domain satisfying the ACCP is a UFD if and only if every irreducible element is prime.
• Any two elements of a UFD have a greatest common divisor and a least common multiple. Here, a greatest common divisor of a and b is an element d which divides both a and b, and such that every other common divisor of a and b divides d. All greatest common divisors of a and b are associated.
• Any UFD is integrally closed. In other words, if R is a UFD with quotient field K, and if an element k in K is a root of a monic polynomial with coefficients in R, then k is an element of R.

Q6) What are the Equivalent conditions for a ring to be a UFD?

A6)

If and only if every height 1 prime ideal is primary, a Noetherian integral domain is a UFD (a proof is given at the end). A Dedekind domain is also a UFD if and only if the ideal class group of the domain is trivial. It is, in fact, a primary ideal domain in this situation.

The following criteria are identical in general for an integral domain A:

1. A is a user-defined function.

2. There is a prime element in every nonzero prime ideal of A. (Kaplansky)

3. The localization meets the ascending chain condition on principal ideals (ACCP). S1A is a UFD, where S is a prime element-generated multiplicatively closed subset of A. (Criteria of Nagata)

4. A fulfils ACCP, and all irreducibles are prime.

5. Every irreducible is prime, and A is atomic.

6. A is a GCD domain (one in which any two items have the same greatest common divisor) that satisfies (ACCP).

7. A is an atomic Schreier domain.

8. A is an atomic and pre-Schreier domain.

Q7) “R be a domain and f a Euclidean function on R” Give highlight on it?

A7)

• R is a principal ideal domain (PID). In fact, if I is a nonzero ideal of R then any element a of I {0} with minimal value (on that set) of f(a) is a generator of I. As a consequence R is also a unique factorization domain and a Noetherian ring. With respect to general principal ideal domains, the existence of factorizations (i.e., that R is an atomic domain) is particularly easy to prove in Euclidean domains: choosing a Euclidean function f satisfying (EF2), x cannot have any decomposition into more than f(x) non-unit factors, so starting with x and repeatedly decomposing reducible factors is bound to produce a factorization into irreducible elements.
• Any element of R at which f takes its globally minimal value is invertible in R. If an f satisfying (EF2) is chosen, then the converse also holds, and f takes its minimal value exactly at the invertible elements of R.
• If the Euclidean property is algorithmic, i.e., if there is a division algorithm that for given a and nonzero b produces a quotient q and remainder r with a = bq + r and either r = 0 or f(r) < f(b), then an extended Euclidean algorithm can be defined in terms of this division operation.

Q8) Explain the relations with prime element with example?

A8)

Prime elements and irreducible elements are not the same thing. (In a commutative ring R, a non-zero non-unit element an is called prime if a|bc for some b and c in R, then a|b or a|c) Every prime element is irreducible in an integral domain, although this is not the case in general. For unique factorization domains, the opposite is true (or, more generally, GCD domains.)

Furthermore, whereas an ideal generated by a prime element is a prime ideal, an ideal created by an irreducible element is not an irreducible ideal in general. If D is a GCD domain and x is an irreducible element of D, then x is prime, and the ideal generated by x is a prime (thus irreducible) ideal of D, as stated above.

Example

In the quadratic integer ring  it can be shown using norm arguments that the number 3 is irreducible. However, it is not a prime element in this ring since, for example,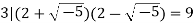

But 3 does not divide either of the two factors.

Q9) Explain the theorem in divisibility in integral domain?

A9)

Let R be a ring. Then R is a domain if and only if for all a,b,c∈R with c≠0 and ac=bc, we have a=b.

Let R be a commutative ring with identity, and let a,b∈R. We say aa divides b and write a∣b if there is a c∈R such that ac=b. We then say that ais a factor of b.

Let R be a domain. We say a nonzero non-unit element a∈R is prime if whenever a∣bc for some b,c∈R, either a|b or a|c.

Let R be a domain. We say a nonzero non-unit element a∈R is irreducible if whenever a=bc for some b,c∈R, one of b or c is a unit

Q10) Let R be a domain and a, b∈R and suppose d is a greatest common divisor of a and b. Then any associate of d is also a greatest common divisor of a and b. Give highlight

A10)

• An integral domain is a commutative ring with no zero-divisors and an identity (1 0). That example, ab = 0 (a = 0) or b = 0 (b = 0). Examples. The integral domain is the ring Z.
• If R = 0 (or 1 = 0), and r is a zero divisor in R, then R is an integral domain.
• An integral domain is a commutative ring with no zero-divisors and identity.

Q11) Consider D = 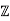[d] = {a + b √ d : a, b ∈ }, where d 6= 1 and not divisible by p2 for a prime. Prove

A11)

Define N(a + b √ d) = |a 2 – db2 |.

Then

• N(x) = 0 if and only if x = 0; N(xy) = N(x)N(y);
• N(x) = 1 if and only if x is a unit;
• If N(x) is prime then x is irreducible in 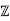[ √ d].

Q12) In D = [−3] = {a + b √ −3 : a, b ∈ 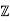}, the element 2 is irreducible, but it is not a prime. Prove

A12)

Proof. If 2 = bc and x, y ∈ D are not units, then 4 = N(2) = N(x)N(y). So, 2 = N(x) = N(a + b √ −3) = a 2 + 3b 2 , a contradiction.

Note that 4 = (1 + √ −3)(1 − √ −3) is divisible by 2, but none of (1 ± √ −3) is divisible by 2.

Q13) Let R = [i] be the ring of Gaussian integers. Define a function by sending a + bi to its norm, which is by definition a2 + b2. Then the ring of Gaussian integers is a Euclidean domain.

A13)

Note first that if z is a complex number, then the absolute value of z, defined as the square root of the product of z with its complex conjugate z¯, is closely related to the norm of z.

In fact if z is a Gaussian integer x + iy, then

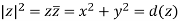
On the other hand, suppose we use polar coordinates, rather than Cartesian coordinates, to represent a complex number,

Then

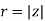
For any pair z1 and z2 of complex numbers, we have

Indeed this is clear, if we use polar coordinates. Now suppose that both z1 and z2 are Gaussian integers. If we square both sides of the equation above, we get

As the absolute value of a Gaussian integer is always at least one, (1) follows easily.

To prove (2), it helps to think about this problem geometrically. First note that one may think of the Gaussian integers as being all points in the plane with integer coordinates. Fix a Gaussian integer α. To obtain all multiples of α = reiθ, that is, the principal ideal (α), it suffices to take this lattice, rotate it through an angle of θ and stretch it by an amount r. With this picture, it is clear that given any other Gaussian integer β, there is a multiple of α, call it qα, such that the square of the distance between β and qα is at most r2/2. Indeed let γ = β/α. Pick a Gaussian integer q such that the square of the distance between γ and q is at most 1/2. Then the distance between β = γα and qα is at most r2/2. Thus we may write

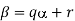
(different r of course) such that d(r) < d(α).

It might help to see a simple example of how this works in practice. Suppose that we take a = 1 + i and b = 4 − 5i. The first step is to construct

Now

So that the inverse of a is

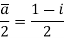
Multiplying by b we get

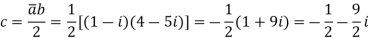
Now we pick a Gaussian integer that is no more than a distance of 1 from c. For example −4i will do (indeed any one of −1 − 5i, −5i, −4i and −1 − 4i will work). This is our quotient q. The error at this point is

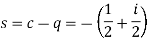
Now multiplying both sides by a, we get

So that

Thus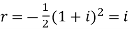 

Clearly

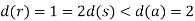
As required.

Q14) Prove that the ring of integers

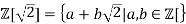of the field () is a Euclidean Domain.

A14)

First of all, it is clear that 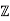[] is an integral domain since it is contained in R.

We use the norm given by the absolute value of field norm.

Namely, for each element

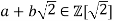define

Then the map N: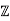[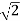]→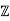≥0 is a norm on .

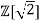Also, it is multiplicative:

Remark that since this norm comes from the field norm of , the multiplicativity of N holds for x,y∈ as well.

We show the existence of a Division Algorithm as follows.

Let

Be arbitrary elements in 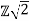, where a,b,c,d∈Z.

We have

Where we put

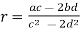and

Let n be an integer closest to the rational number r and let m be an integer closest to the rational number s, so that

Let

Then we have

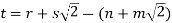
It follows that

Thus we have

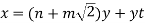with

We have

It follows from the multiplicativity of the norm N that

Thus the expression (*) gives a Division Algorithm with quotient 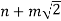 and remainder yt.

Q15) Let R be a finite commutative ring with identity 1. Prove that every prime ideal of R is a maximal ideal of R.

A15)

Let I be a prime ideal of the ring R. Then the quotient ring R/I is an integral domain since II is a prime ideal. Since R is finite, R/I is also finite.

By Problem Finite Integral Domain is a Field, any finite integral domain is a field. This yield that R/I is a field, and hence I is a maximal ideal.

Q16) Is it true that a set of nilpotent elements in a ring R is an ideal of R?

If so, prove it. Otherwise give a counterexample.

A16)

We give a counter example.

Let R be the noncommutative ring of 2×2 matrices with real coefficients.

Consider the following matrices A,B in R.

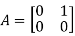and B=

Direct computation shows that A2 and B2 are the zero matrix, hence A,B are nilpotent elements.

However, the sum

Is not nilpotent as we have

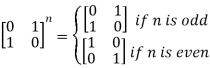
Hence the set of nilpotent elements in RR is not an ideal as it is not even an additive abelian group.

Q17) Let R be a commutative ring with 1.

Prove that if every proper ideal of R is a prime ideal, then R is a field.

A17)

As the zero ideal (0) of R is a proper ideal, it is a prime ideal by assumption.
Hence R=R/{0} is an integral domain.

Let aa be an arbitrary nonzero element in R.

We prove that aa is invertible.

Consider the ideal (a2) generated by the element a2.

If (a2)=R, then there exists b∈R such that 1=a2b as 1∈R=(a2).

Hence we have 1=a(ab) and aa is invertible.

Next, if (a2) is a proper ideal, then (a2) is a prime ideal by assumption.

Since the product a⋅a=a2 is in the prime ideal (a2), it follows that a∈(a2).

Thus, there exists b∈R such that a=a2b.

Equivalently, we have a(ab−1)=0.

We have observed above that R is an integral domain. As a≠0, we must have ab−1=0, and hence ab=1.

This implies that a is invertible.

Therefore, every nonzero element of R is invertible.

Hence R is a field.

Q18) Let R be an integral domain and let I be an ideal of R.

Is the quotient ring R/I an integral domain?

A18)

The quotient ring R/I of an integral domain is not necessarily an integral domain.

Consider, for example, the ring of integers 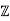 and ideal I=4.

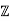Note that  is an integral domain.

We claim that the quotient ring 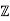/4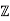 is not an integral domain.

In fact, the element 2+4 is a nonzero element in /4.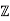

However, the product

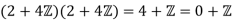
Is zero in /4.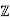

This implies that 2+4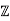 is a zero divisor, and thus 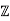/4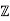 is not an integral domain.

Q19) Let R be a ring with 1≠0. Let a,b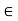R such that ab=1.

(a) Prove that if a is not a zero divisor, then ba=1.

(b) Prove that if b is not a zero divisor, then ba=1.

A19)

(a) Prove that if a is not a zero divisor, then ba=1.

Suppose that a is not a zero divisor. We compute

By distributivity

By ab=1

Since a is not a zero divisor, this yields that ba−1=0, and hence ba=1.

(b) Prove that if b is not a zero divisor, then ba=1.

Suppose that b is not a zero divisor. We calculate

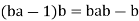 by distributivity

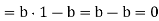 by ab=1

As bb is not a zero divisor, the equality (ba−1)b=0 implies that ba−1=0.

Hence we have ba=1.