Unit - 2

Subspaces

Q1) Let (X, d) be a metric space and Y a subspace of X. Let z 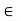 Y and r > 0. Then

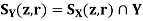
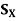Where (z, r) (respectively (z, r)) denotes the ball with centre z and radius r in Y (respectively X). Prove.

A1)

Here we have-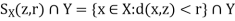

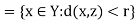
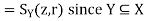
Let 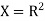and .

Here the open ball in Y with centre (1, 0) and radius 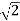is the entire space of Y.

Q2) Let Y be a subspace of a metric space (X, d). Every subset of Y that is open in Y is also open in X if and only if Y is open in X. Prove.

A2)

Suppose every subset of Y open in Y is also open in X. We want to show that Y is open in X. Since Y is an open subset of Y, it must be open in X. Conversely, suppose Y is open in X. Let Z be an open subset of Y. By above result (given in note), there exists an open subset G of X such that Z = G 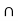Y. Since G and Y are both open subsets of X, their intersection must be open in X, i.e., Z must be open in X.

Q3) If Y is a nonempty subset of a metric space (X, d), and (Y, d) is complete, then Y is closed in X. Prove.

A3)

Let x be any limit point of Y. Then x is the limit of a sequence in Y. The sequence is Cauchy, and hence, by assumption, converges to a point y of Y. But following Definition 1.3.2, y = x.

Therefore, x 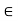Y. This shows that Y is closed in X.

Q4) Define local base.

A4)

Let (X, d) be a metric space and x 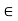X. Let 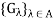be a family of open sets, each containing x. The family  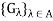 is said to be a local base at x if, for every nonempty open set G containing x, there exists a set 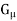in the family such that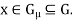

Q5) In any metric space, there is a countable base at each point. Prove.

A5)

Let (X, d) be a metric space and x 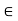X. The family of open balls centred at x

And having rational radii, i.e., {S(x, 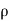): 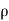rational and positive} is a countable base at

x. In fact, if G is an open set and x 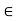G, then by the definition of an open set, there

Exists an > 0 (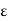 depending on x) such that 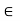x S(x, 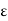) 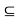G. Let 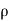be a positive

Rational number less than 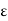. Then

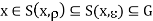
Q6) The collection {S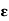(x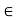, ): x X, 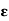> 0} of all open balls in X is a base for the open sets of X. Prove.

A6)

Let G be a nonempty open subset of X and let x 2 G. By the definition of an open subset, there exists a positive e(x) (depending upon x) such that

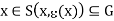
Which is the proof.

Q7) What do you understand by second countable metric space?

A7)

A metric space is said to be second countable (or satisfy the second axiom of countability) if it has a countable base for its open sets.

The reason for the name second countable is that the property of having a countable base at each point.

Q8) Define open cover.

A8)

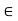Let (X, d) be a metric space and G be a collection of open sets in X. If for each x X there is a member G G’ such that x 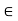G, then G’ is called an open cover (or open covering) of X. A sub-collection of G’ which is itself an open cover of X is called a sub-cover.

Q9) What is separable metric space?

A9)

The metric space X is said to be separable if there exists a countable, everywhere dense set in X. In other words, X is said to be separable if there exists in X a sequence 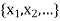such that for every x 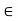X, some sequence in the range of the above converges to x.

Q10) Let (X, d) be a metric space and Y 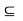X. If X is separable, then Y with the induced metric is separable, too. Prove.

A10)

Let E = {xi : i =  1, 2, . . . } be a countable dense subset of X. If E is contained in

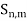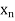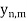
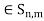
Y, then there is nothing to prove. Otherwise, we construct a countable dense subset of Y whose points are arbitrarily close to those of E. For positive integers n and m, let =  S(, 1/m) and choose  Y whenever this set is nonempty. We show that the countable set {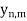: n and m positive integers} of Y is dense in Y.

For this purpose, let y Y and 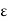> 0. Let m be so large that 1/m < 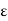/2 and find   2 S(y, 1/m). Then y 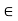  Y and

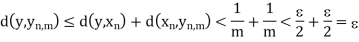
Thus, 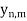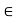S(y, 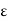). Since y 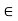Y and 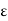> 0 are arbitrary, the assertion is proved.

Q11) Define Baire’s category theorem.

A11)

Let (X, d) be a complete metric space.

(1) Let 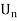, be open dense subsets of X, for n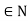. Then 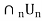is dense in X.

(2) Let 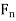, be nonempty closed subsets of X such that X = 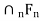Then at least one of 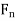's has nonempty interior. In other words, a complete metric space cannot be a countable union of nowhere dense closed subsets