Unit - 2

Matrix representation of a linear transformation

Q1) Define linear transformation.

A1)

Let V and U be vector spaces over the same field K. A mapping F : V 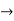U is called a linear mapping or linear transformation if it satisfies the following two conditions:

(1) For any vectors v; w 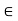V, F(v + w) = F(v) + F(w)

(2) For any scalar k and vector v 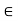V, F(kv) = k F(v)

Now for any scalars a, b 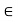   K and any vector v, w  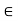  V, we obtain

F (av + bw) = F(av) + F(bw) = a F(v) + b F(w)

Q2) What do you understand by the matrix representation of linear transformation?

A2)

Ordered basis- Let V be a finite-dimensional vector space. An ordered basis for V is a basis for V endowed with a specific order; that is, an ordered basis for V is a finite sequence of linearly independent vectors in V that generates V.

Definition. Let 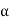= {,,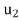 . . . , 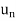} be an ordered basis for a finite dimensional

Vector space V. For x ∈ V, let 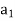, , 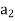. . . , 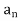be the unique scalars

Such that

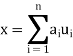
We define the coordinate vector of x relative to 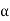, we denote it by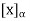

Q3) let given by

A3)

Let 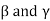be the standard ordered bases for 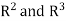, respectively. Now

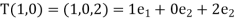
And

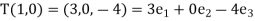
Hence

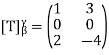
If we suppose 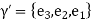, then

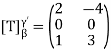
Q4) 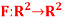be the linear operator defined by F(x, y) = (2x + 3y, 4x – 5y).

Find the matrix representation of F relative to the basis S = { } = {(1, 2), (2, 5)}

A4)

(1) First find F(, and then write it as a linear combination of the basis vectors and 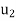. (For notational convenience, we use column vectors.) We have

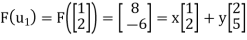
And

X + 2y = 8

2x + 5y = -6

Solve the system to obtain x = 52, y =-22. Hence,

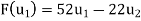
Now

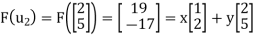
X + 2y = 19

2x + 5y = -17

Solve the system to obtain x = 129, y =-55. Hence,

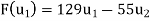
Now write the coordinates of 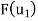and 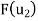as columns to obtain the matrix

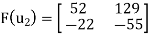
Q5) 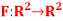be the linear operator defined by F(x, y) = (2x + 3y, 4x – 5y).

Find the matrix representation of F relative to the basis S = { } = {(1, -2), (2, -5)}

A5)

Step 0 - First find the coordinates of 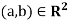relative to the basis S. We have

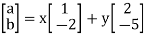
Or

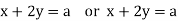
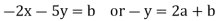
Solving for x and y in terms of a and b yields x = 5a + 2b,  y = -2a – b, thus

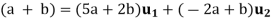
Step 1- Now we find and write it as a linear combination of and using the above formula for (a, b). And then we repeat the process for 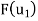. We have

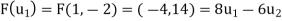
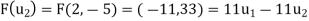
Step 2-  Now, we write the coordinates of and 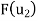as columns to obtain the required matrix:

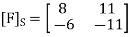
Q6) Define left inverse and right inverse.

A6)

Let f : S → T be any function. Then

1. A function g : T → S is called a left inverse of f if (g o f)(x) = x, for all x ∈ S. That is, g o f = Id, the identity function on S.

2. A function h : T → S is called a right inverse of f if (f o h)(y) = y, for all y ∈ T. That is, f 0 h = Id, the identity function on T.

3. f is said to be invertible if it has a right inverse and a left inverse.

Q7) Let V, W, and Z be vector spaces over the same field F, and let T: V → W and U: W → Z be linear. Then UT: V → Z is linear.

A7)

Let x, y ∈ V and a ∈ F. Then UT(ax + y) = U(T(ax + y)) = U(aT(x) + T(y))

= aU(T(x)) + U(T(y)) = a(UT)(x) + UT(y).

Q8) What do you understand by invertible transformation?

A8)

Let V and W be vector spaces, and let T: V → W be linear.

A function U: W → V is said to be an inverse of T if TU = 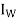and UT = IV.

If T has an inverse, then T is said to be invertible. As noted in Appendix B,

If T is invertible, then the inverse of T is unique and is denoted by .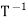

The following conditions hold for invertible functions T and U.

1. = .

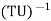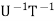2. 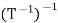= T; in particular, is invertible.

3. Let T: V → W be a linear transformation, where V and W are finite dimensional spaces of equal dimension. Then T is invertible if and only

If rank(T) = dim(V).

Q9) Let V and W be vector spaces, and let T: V → W be linear and invertible. Then T−1: W → V is linear.

A9)

Let 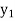, 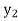∈ W and c ∈ F. Since T is onto and one-to-one, there

Exist unique vectors x1 and x2 such that T(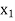) = 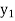and T(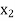) = 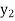. Thus

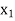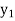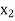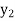= () and = (); so

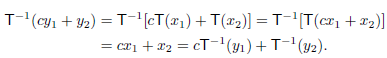
Q10) Let V and W be finite-dimensional vector spaces (over the same field). Then V is isomorphic to W if and only if dim (V) = dim (W).

A10)

Suppose that V is isomorphic to W and that T: V → W is an isomorphism from V to W. By the lemma, we have that dim(V) = dim(W).

Now suppose that dim(V) = dim(W), and let 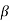= {v1, v2, . . . , vn}. And = {w1, w2, . . . , wn} be bases for V and W, respectively

There exists T: V → W such that T is linear and T(vi) = wi for i = 1, 2, . . . , n. We have

R(T) = span(T()) = span(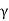) = W.

So T is onto.

We have that T is also one-to-one. Hence T is an isomorphism.

Q11) what is called linear functional?

A11)

Let V be a vector space over a field K. A mapping 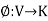is called a linear functional if, for every u, v 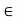V and every a, b

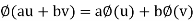
Note- a linear functional on V is a linear mapping from V into K.

The set of linear functionals on a vector space V over a field K is also a vector space over K, with addition and scalar multiplication defined by

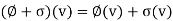
And

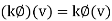
Where 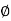and are linear functionals on V and k belongs to K. This space is called the dual space of V and is denoted by V*.

Q12) What is dual basis?

A12)

Definition of dual basis:

We call the ordered basis β∗ = {f1, f2, . . . , fn} of V∗ that satisfies fi(xj) = 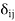(1 ≤ i, j ≤ n) the dual basis of β.

Note- Let V be a finite-dimensional vector space with dual space V*. Then every ordered basis for V* is the dual basis for some basis for V.

Q13) What are annihilators?

A13)

Let W be a subset (not necessarily a subspace) of a vector space V. A linear functional 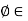V* is called an annihilator of W if 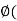w) = 0 for every w 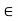W, that is, if 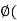w) = {0}. We show that the set of all such mappings, denoted by 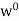and called the annihilator of W, is a subspace of V*. Clearly, 0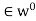

Now suppose 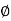,  . Then, for any scalars a, b 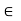K and for any 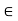w W,

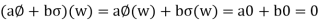
Thus 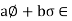 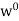 and so 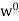is a subspace of V*.

Q14) What is field?

A14)

A field F is a set on which two operations + and · (called addition and multiplication, respectively) are defined so that, for each pair of elements x, y in F, there are unique elements x+y and x·y in F for which the following conditions hold for all elements a, b, c in F.

(1) a + b = b + a and a·b = b·a

(commutativity of addition and multiplication)

(2) (a + b) + c = a + (b + c) and (a·b)·c = a· (b·c)

(associativity of addition and multiplication)

(3) There exist distinct elements 0 and 1 in F such that

0 + a = a and 1·a = a

(existence of identity elements for addition and multiplication)

(4) For each element a in F and each nonzero element b in F, there exist

Elements c and d in F such that

a + c = 0 and b·d = 1

(existence of inverses for addition and multiplication)

(5) a·(b + c) = a·b + a·c

(distributivity of multiplication over addition)