Unit - 4

Game theory

Q1) Explain a game.

A1)

A game is a contest involving two or more than two persons (competitors) each of whom wants to win. A theory of games gives a series of mathematical models that can be useful in explaining decision-making concepts, where two or more persons or competitors are involved under conditions of conflict and competition.

A player may be an individual, individuals, or an organization.

Game theory was introduced by John Von Neumann and Oscar Morgenstern in 1944.

Business decisions in a competitive situation do not depend on the decisions of the organization alone but on the interaction between the decisions of the organization and those of the competitors. Each firm tries to select and execute its strategies and aims to maximize its gains at the cost of its opponents. Game theory deals with problems where actions and interactions of competing firms give rise to conditions of business conflict. In other words, Game Theory is a body of knowledge which is concerned with the study of decision-making in situations where two or more rational opponents are involved under conditions of competition and conflicting interest.

Q2) Define game theory.

A2)

Game theory is a body of knowledge that deals with making decisions when two or more intelligent and rational opponents are involved under conditions of conflict or competition. The competitors in the game are called players.

Note-

The mathematical approach of Von Neumann utilizes the Minimax principle, which involves the fundamental idea of minimization of the maximum losses. Many of the competitive problems can be handled by the game theory but not all the competitive problems can be analyzed with the game theory.

Q3) Write down the factors of game theory.

A3)

Number of players:

If a game involves only two players, then it is called a two-person game. However, if the number of players are more, the game is referred to as n-person game.

Sum of gains and losses:

If, in a game, the sum of the gains to one player is exactly equal to the sum of losses to another player, so that, the sum of the gains and losses equals zero, then the game is said to be a zero-sum game. Otherwise it is said to be non-zero sum game

Strategy:
The strategy for a player is the list of all possible actions that are likely to be adopted by him for ever outcome.

The outcome resulting from a particular strategy is also known to the players in advance and is expressed in terms of numerical values.

The particular strategy that optimizes a player’s gains or losses, without knowing the competitor’s strategies, is called optimal strategy.

A player follows two types of strategies:

Pure Strategy:

A particular strategy that a player chooses to play repeatedly regardless of other player’s strategy, is referred as pure strategy. The objective of the players is to maximize their gains or minimize their losses.

Mixed Strategy:

A set of strategies that a player chooses on a particular move of the game with some fixed probability are called mixed strategies.

Q4) What is payoff matrix?

A4)

The payoffs in terms of gains or losses, when players select their particular strategies, can be represented in the form of a matrix, called the payoff matrix.

If player P has m strategies represented by the letters: P1, P2, . . ., Pm and player Q has n strategies represented by the letters: Q1, Q2, . . ., Qn. The numbers m and n need not be equal. The total number of possible outcomes is therefore m × n. It is assumed that each player not only knows his own list of possible strategies but also of his competitor. For convenience, it is assumed that player P is always a gainer whereas player Q a loser. Let aij be the payoff that player P gains from player Q if player P chooses strategy i and player Q chooses strategy j. Then the payoff matrix is shown in the-

Player P’s strategy	Player P’s strategy                                       …...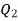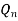
. . .	.                                                                      . .                                     .                                . .                                       .                              . .

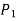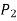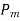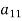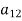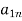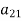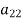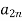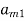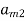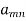Since player P is assumed to be the gainer, therefore he wishes to gain as large a payoff aij as possible, player Q on the other hand would do his best to reach as small a value of aij as possible. Of course, the gain to player Q and loss to P must be – aij.

Q5) What do you understand by a saddle point?

A5)

A saddle point in a pay-off matrix corresponds to that element of the matrix which represents the ‘Maxmin’ value of a player and Minimax value of his opponent. For this we find Maximum element of each column and then find the Minimum value of column Maxima known as Minimax. Similarly, we identify minimum element of each row and then find the Maximum of those entries known as Maximin. If Minimax = Maximum of those entries  known as Maximin. If Minimax = Maximin, then saddle point exists and the value of the game is equal to Minimax to Maximin. If Minimax  Maximin, then no saddle point exists. If Minimax = Maximin, then the pure strategies are called optimum strategies. Usually Maximin  value of the game  Minimax. If Maximin = Minimax = 0, the game is fair. If Maximin = Minimax, the game is strictly determinable. The value of the game is the average pay-off that would suit the game was played over and over again.

Q6) What are games with mixed strategies or game without saddle point?

A6)

In certain cases, no saddle point exists, which means maximin value is unequal to minimax value.

In all such cases, players must choose the mixture of strategies to find the value of game and an optimal strategy.

The value of game obtained by the use of mixed strategies represents the least payoff, which player

A can expect to win and the least which player B can expect to lose. The expected payoff to a player in

a game with payoff matrix [aij] of order m × n is defined as:

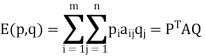
Where P = ( p1, p2, . . ., pm) and Q = (q1, q2, . . ., qn) are the probabilities (or relative frequency with which a strategy is chosen from the list of strategies) associated with m strategies of player A and n strategies of player, B respectively, where p1 + p2 + . . . + pm = 1 and q1 + q2 + . . . + qn = 1.

Q7) Two MNC’s A and B make plasma and LCD television sets. Company A can make either 150 plasma sets in a week or an equal number of LCD sets, and make a profit of Rs 400 per plasma set, or 150 plasma and 150 LCD sets, or 300 LCD sets per week. It also has the same profit margin on the two sets as A. Each week there is a market of 150 plasma sets and 300 LCD sets and the manufacturers would share market in the proportion in which they manufacture a particular type of set. Write the pay-off matrix of A per week. Obtain graphically A’s and B’s optimum strategies and value of the game.

A7)

For company A, the strategies are:

A1: make 150 plasma sets, A2: make 150 LCD sets. For company B, the strategies are:

B1: make 300 plasma sets, B2: make 150 plasma and 150 LCD sets.

B3: make 300 LCD sets.

For the combination A1B1, the profit to company A would be: {150/(150 + 300)} × 150 × 400 = Rs 20,000 wherein 150/(150 + 300) represents share of market for A, 150 is the total market for plasma television sets and 400 is the profit per set. In a similar manner, other profit figures may be obtained as shown in the following pay-off matrix:

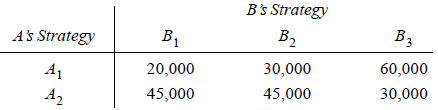
This pay-off table has no saddle point. Thus to determine optimum mixed strategy, the data are plotted on Graph given below-

Lines joining the pay-offs on axis A1 with the pay-offs on axis A2 represents each of B’s strategies. Since company A wishes to maximize his minimum expected pay-off, we consider the highest point of intersection, P on the lower envelope of A’s expected payoff equation. This point P represents the maximum expected value of the game. The lines B1 and B3 passing through P, define the strategies which company B needs to adopt. The solution to the original 2 × 3 game, therefore, reduces to that of the simpler game with 2 × 2 pay-off matrix as follows:

The optimal mixed strategies of player A are: A1 = 3/11, A2 = 8/11. Similarly, the optimal mixed strategies for B are: B1 = 6/11, B2 = 0, B3 = 5/11. The value of the game is V = 38,182.

Q8) Give the explanation of the solution of game by using LP.

A8)

We can solve the two-person zero-sum by using linear programming.

Linear programming helps to solve the mixed-strategy games of larger dimension payoff  matrix.

Consider a payoff matrix of size m × n. Let aij be the element in the ith row and jth column of game payoff matrix, and letting pi be the probabilities of m strategies (i = 1, 2, . . ., m) for player A. Then, the expected gains for player A, for each of player B’s strategies will be:

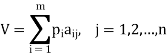
The aim of player A is to select a set of strategies with probability pi (i = 1, 2, . . ., m) on any play of game such that he can maximize his minimum expected gains.

Now to obtain values of probability pi, the value of the game to player A for all strategies by player

B must be at least equal to V. Thus to maximize the minimum expected gains, it is necessary that:

….

….

….

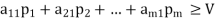
Where

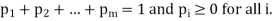
Dividing both sides of the m inequalities and equation by V the division is valid as long as V > 0.

In case V < 0, the direction of inequality constraints must be reversed. But if V = 0, the division would be meaningless. In this case a constant can be added to all entries of the matrix, ensuring that the value of the game (V ) for the revised matrix becomes more than zero. After optimal solution is obtained, the true value of the game is obtained by subtracting the same constant value. Let pi/V = xi, (≥0), we then have

….

….

….

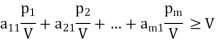
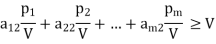
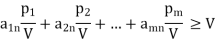
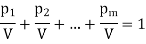
Since the objective of player A is to maximize the value of the game, V, which is equivalent to minimizing 1/V, the resulting linear programming problem can be stated as:

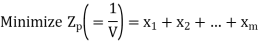
Subject to the constraints

….

….

….

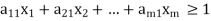
And

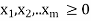
Where

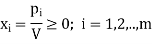
Similarly, Player B has a similar problem with the inequalities of the constraints reversed, i.e. minimize the expected loss. Since minimizing V is equivalent to maximizing 1/V, therefore, the resulting linear programming problem can be stated as:

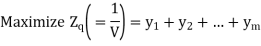
Subject to the constraints

….

….

….

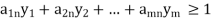
And

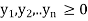
Where

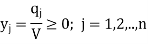
Q9) Give some applications of game theory.

A9)

(a) In a competitive market, sometimes companies wage a price war. What should be the bid to win major government contract in the face of competition from several contractors.

(b) An equipment dealer and a customer may be at Cross purposes regarding price but they would both want to close a mutual advantageous deal. Similarly, in a collective bargaining process, the trade union and the management of a company share the objective of striking at a mutually advantageous deal and keep the company operations going.

(c) Suppose a firm wants to introduce a new product in the market, to get a bigger share in the market, the marketing manager of the firm would be interested to know the best possible strategies of a competitor who is also trying to introduce product with different strategies e.g., price reduction, better quality, etc.

Q10) What are the limitations of games in competition?

A10)

1. In practice, the two competitors rarely have equal information or intelligence.

2. There may be situations in the managerial decisions when both the players may lose or gain. Hence, it may not be zero-sum game.

3. Most of the competitive situations in which managerial decisions are taken are never really two-person games as government or other bodies are always present as third or fourth party in the game.

4. The technique of solving games involving mixed strategies is very complicated specially for problems having large payoff matrices.

5. The principle of minimax implies that the businessman and his chances of maximum loss but a dynamic businessman is always after profit and tries to maximize his gains or profit even by taking greater risks.