Unit - 1
Functions of several variables
Q1) What do you understand by the functions of two variables?
A1)
R denotes the set of real numbers. Let’s D is a collection of pairs of real numbers (x , y), which means D is a subset of R × R.
Then a real valued function of two variables of f is a rule that assign to each point (x, y) in D a unique real number denoted by f(x, y).
The set D is called the domain of f.
The set [ f(x, y): (x, y) belongs to D ], which is the set of values the function f takes, is called range of f.
Here we generally use the letter z to denote the value that a function of two variables takes,
Then we will have,
z = f(x, y)
Here we will call that z is the dependent variable and x and y are independent variables.
Q2) Evaluate 
A2)
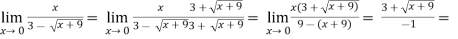 -6.
-6.
Q3) Evaluate 
A3)

Q4) Evaluate 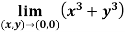
A4)
1. 
2. 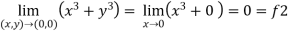
Here f1 = f2
3. Now put y = mx, we get
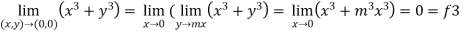
Here f1 = f2 = f3
Now put y = mx²
4. 
Therefore,
F1 = f2 = f3 =f4
We can say that the limit exists with 0.
Q5) Evaluate the following-
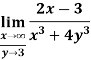
A5)
First we will calculate f1 –

Here we see that f1 = 0
Now find f2,

Here , f1 = f2
Therefore the limit exists with value 0.
Q6) Calculate 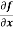 and
and  for the following function
for the following function
f(x , y) = 3x³-5y²+2xy-8x+4y-20
A6)
To calculate 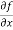 treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
 =
=  [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
= 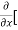 3x³] -
3x³] - 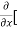 5y²] +
5y²] +  [2xy] -
[2xy] -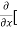 8x] +
8x] + 4y] -
4y] -  20]
20]
= 9x² - 0 + 2y – 8 + 0 – 0
= 9x² + 2y – 8
Similarly partial derivative of f(x,y) with respect to y is:
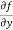 =
= 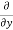 [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
=  3x³] -
3x³] -  5y²] +
5y²] +  [2xy] -
[2xy] - 8x] +
8x] + 4y] -
4y] - 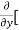 20]
20]
= 0 – 10y + 2x – 0 + 4 – 0
= 2x – 10y +4.
Q7) Calculate 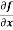 and
and  for the following function
for the following function
f( x, y) = sin(y²x + 5x – 8)
A7)
To calculate 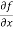 treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
 [sin(y²x + 5x – 8)]
[sin(y²x + 5x – 8)]
= cos(y²x + 5x – 8)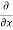 (y²x + 5x – 8)
(y²x + 5x – 8)
= (y² + 50)cos(y²x + 5x – 8)
Similarly partial derivative of f(x,y) with respect to y is,
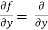 [sin(y²x + 5x – 8)]
[sin(y²x + 5x – 8)]
= cos(y²x + 5x – 8) (y²x + 5x – 8)
(y²x + 5x – 8)
= 2xy cos(y²x + 5x – 8)
Q8) If,

Then find.

A8)
We have
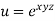

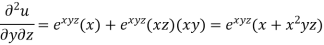


Q9) If z = 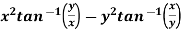
Then prove that-

A9)
Here we have-

Then
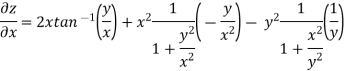
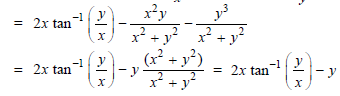
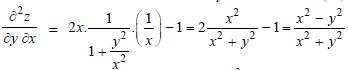
Q10) What is chain rule for partial derivatives?
A10)
Suppose u = f (x, y) and x and y are themselves functions of a single independent variable
t. Then the dependent variable f may be considered as truly a function of the one independent variable t via the intermediate variables x, y. Now the derivative of f with respect to ‘t ’ is known as the total derivative of f and is given by

Note- if u = f (x, y, z) and x = x(t ), y = y(t ), z = z(t ) then the total derivative of f is
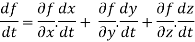
And we can find the this result for more than three variables in same way.
Q11) if w = x² + y – z + sint and x + y = t, find
(a)  y,z
y,z
(b) 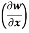 t, z
t, z
A11)
With x, y, z independent, we have
t = x + y, w = x²+ y - z + sin (x + y).
Therefore,
 y,z = 2x + cos(x+y)
y,z = 2x + cos(x+y) (x+y)
(x+y)
= 2x + cos (x + y)
With x, t, z independent, we have
Y = t-x, w= x² + (t-x) + sin t
Thus
 t, z = 2x – 1
t, z = 2x – 1
Q12) If φ(cx – az, cy – bz) = 0 then show that ap + bq = c
Where p =  q =
q = 
A12)
We have,
φ( cx – az , cy – bz) = 0
φ( r , s) = 0
Where,

We know that,
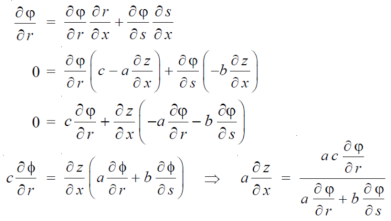
Again we do,
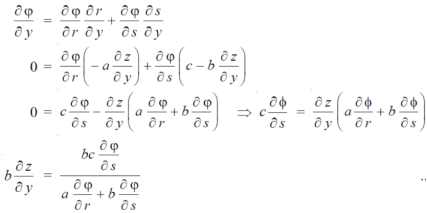
By adding the two results, we get
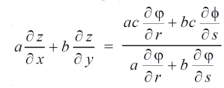

Q13) If z is the function of x and y , and x = 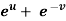 , y =
, y = 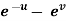 , then prove that,
, then prove that,
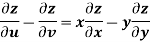
A13)
Here , it is given that, z is the function of x and y & x , y are the functions of u and v.
So that,
 ……………….(1)
……………….(1)
And,
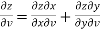 ………………..(2)
………………..(2)
Also there is,
x =  and y =
and y =  ,
,
Now,
 ,
, 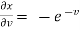 ,
, 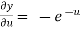 ,
, 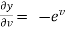
From equation(1) , we get
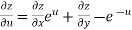 ……………….(3)
……………….(3)
And from eq. (2) , we get
 …………..(4)
…………..(4)
Subtracting eq. (4) from (3), we get
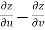 =
=  )
)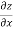 – (
– (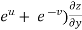
= x
Q14) State and prove the sufficient condition for differentiability.
A14)
Statement- Suppose  there exists a neighborhood N(say) of (a, b) at every point of which
there exists a neighborhood N(say) of (a, b) at every point of which 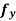 exists. We take (a + h, b + k), a point of this neighborhood so that (a + h, b),(a, b + k) also belongs to N.
exists. We take (a + h, b + k), a point of this neighborhood so that (a + h, b),(a, b + k) also belongs to N.
Proof:
Since ∂f /∂y is continuous at (a, b), there exists a neighborhood N(say) of (a, b) at every point of which  exists. We take (a + h, b + k), a point of this neighborhood so that (a + h, b),(a, b + k) also belongs to N
exists. We take (a + h, b + k), a point of this neighborhood so that (a + h, b),(a, b + k) also belongs to N
We write f(a + h, b + k) − f(a, b) = {f(a + h, b + k) − f(a + h, b)} + {f(a + h, b) − f(a, b)}. Consider a function of one variable φ(y) = f(a + h, y).
Since  exists in N, φ(y) is differentiable with respect to y in the closed interval [b, b+k] and as such we can apply Lagrange’s Mean Value Theorem, for function of one variable y in this interval and thus obtain
exists in N, φ(y) is differentiable with respect to y in the closed interval [b, b+k] and as such we can apply Lagrange’s Mean Value Theorem, for function of one variable y in this interval and thus obtain
φ(b + k) − φ(b) = kφ’ (b + θk), 0 < θ < 1
= k (a + h, b + θk)
(a + h, b + θk)
f(a + h, b + k) − f(a + h, b) = k (a + h, b + θk), 0 < θ < 1.
(a + h, b + θk), 0 < θ < 1.
Now, if we write 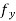 (a + h, b + θk) −
(a + h, b + θk) − 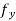 (a, b) =
(a, b) =  (a function of h, k)
(a function of h, k)
Then from the fact that 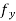 is continuous at (a,b). We may obtain
is continuous at (a,b). We may obtain
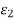 → 0 as (h, k) → (0, 0).
→ 0 as (h, k) → (0, 0).
Again because 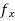 exists at (a, b) implies
exists at (a, b) implies
f(a + h, b) − f(a, b) = h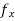 (a, b) +
(a, b) +  ,
,
Where 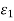 → 0 as h → 0. Combining all these we get
→ 0 as h → 0. Combining all these we get

Where  ,
, 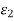 are functions of (h, k) and they tend to zero as (h, k) → (0, 0).
are functions of (h, k) and they tend to zero as (h, k) → (0, 0).
Hence, f(x, y) is differentiable at (a, b).
Q15) If 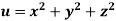 where
where  then find the value of
then find the value of  ?
?
A15)
Given 
Where 
By chain rule
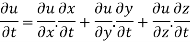
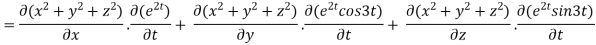

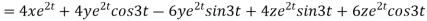
Now substituting the value of x ,y,z we get
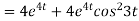 -6
-6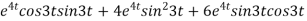

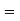 8
8
Q16) If then calculate
then calculate 
A16) Given 
By Chain Rule




Putting the value of u = 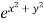
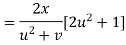
Again partially differentiating z with respect to y
By Chain Rule
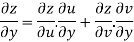

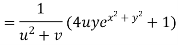
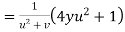 by substituting value
by substituting value 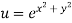

Q17) If 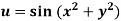 where the relation is
where the relation is 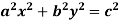 .
.
Find the value of 
A17)
Let the given relation is denoted by 
We know that 
Differentiating u with respect to x and using chain rule

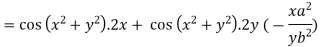

Q18) Find the directional derivative of 1/r in the direction  where
where 
A18)
Here 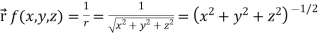
Now,


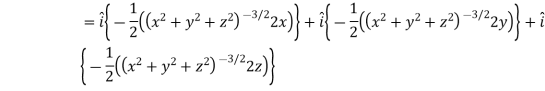
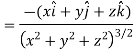
And 
We know that-

So that-
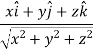
Now,
Directional derivative = 
Q19) Find the directional derivatives of 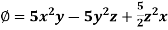 at the point P(1, 1, 1) in the direction of the line
at the point P(1, 1, 1) in the direction of the line 
A19)
Here
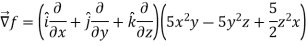

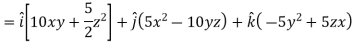

Direction ratio of the line 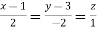 are 2, -2, 1
are 2, -2, 1
Now directions cosines of the line are-

Which are 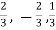
Directional derivative in the direction of the line-

Q20) Prove that 
A20)
First we will take left hand side
L.H.S = 
= 
= 
= 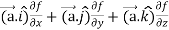
Now taking R.H.S,
R.H.S. = 
= 
= 
Here- L.H.S. = R.H.S.
Q21) If f and g are two scalar point functions, then prove that
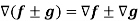
A21)
L.H.S 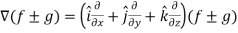
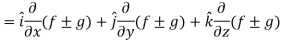

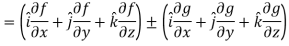
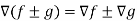
Hence proved
Q22) If 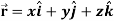 , then show that
, then show that
1. 
2. 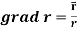
A22)
Suppose  and
and 

Now taking L.H.S,

Which is 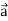
Hence proved.
2. 
So that
