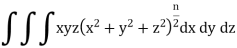Unit - 3
Triple integrals
Q1) Evaluate  , where dA is the small area in xy-plane.
, where dA is the small area in xy-plane.
A1)
Let, I = 
= 
= 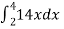
= 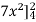
= 84 sq. Unit.
Which is the required area.
Q2) What do you understand by triple integrals?
A2)
Let f(x,y,z) be a function which is continuous at every point of the finite region (Volume V) of three dimensional space. Divide the region V into n sub regions of respective volumes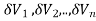 . Let (
. Let ( ) be a point in the
) be a point in the 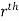 sub region then the sum:
sub region then the sum:
 =
= 
Is called triple integration of f(x, y, z) over the region V provided limit on R.H.S of above Equation exists.

Note-
V is said to be a regular three-dimensional domain if-
(i) Every straight line parallel to z-axis and drawn through an interior point of V cuts the surface S at two points
(ii) Entire V is projected on the xy-plane into a regular two-dimensional domain D.
Q3) Evaluate

A3)
First integrating with respect to z, we get
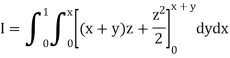

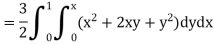
Integrating now with respect to y, we get
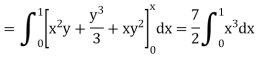
Now we integrate with respect to x
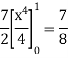
Q4) Evaluate

A4)
Let
I = 
= 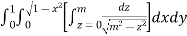
(Assuming m =  )
)
=  dxdy
dxdy
= 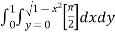
=
=  dx
dx
=  dx
dx
= 
=
I =
Q5) Evaluate

A5)




Q6) Evaluate
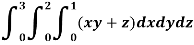
A6)

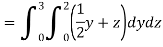
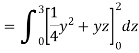
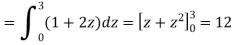
Q7) Evaluate

A7)

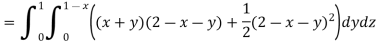



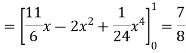
Q8) Find Volume of the tetrahedron bounded by the co-ordinates planes and the plane

A8)
Volume =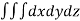 ………. (1)
………. (1)
Put 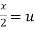 ,
, 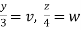
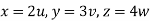
From equation (1) we have
V = 
=24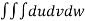
=24 (u+v+w=1) By Dirichlet’s theorem.
(u+v+w=1) By Dirichlet’s theorem.
=24 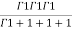
= =
= = 4
= 4
Volume = 4
Q9) Find the total mass of the region in the cube 0 ≤ x ≤ 1, 0 ≤ y ≤ 1, 0 ≤ z ≤ 1 with density at any point given by xyz.
A9)
We know that

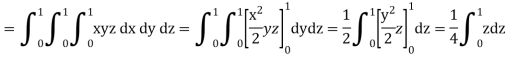

Q10) Calculate the volume of the solid bounded by the following surfaces:
z = 0, x^2 + y^2 = 1, x + y + z = 3
A10)

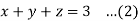
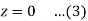
The volume then

On putting x = r cos  , y = r sin
, y = r sin  , dx dy = r d
, dx dy = r d dr, we get
dr, we get

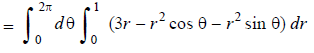
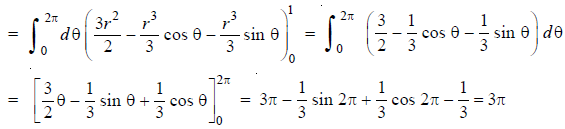
Q11) If the density at any point of a non-uniform circular lamina of radius’ a’ varies as its distance from a fixed point on the circumference of the circle then find the mass of lamina.
A11)

Take the fixed point on the circumference of the circle as origin and diameter through it as x axis. The polar equation of circle 
And density .
.
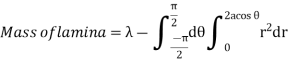

Q12) Find mean value and R.M.S. Value of the ordinate of cycloid
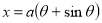 ,
,  over the range
over the range  to
to  .
.
A12)
Let P(x,y) be any point on the cycloid . Its ordinate is y.
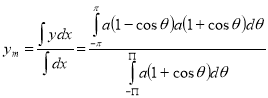
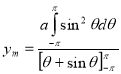
= 
=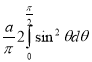
=
R.M.S. Value= 

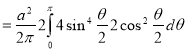
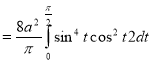
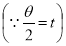


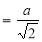
Q13) Evaluate the integral-
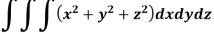
A13)
First we convert the given integral into spherical polar co-ordinates. By putting
x = r sin 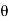 cos
cos 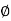
y = r sin 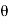 sin
sin 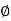
z = r cos 


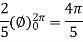
Q14) Evaluate-
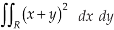
Where-
R is the region bounded by a parallelogram- x + y = 0, x + y = 2, 3x – 2y = 0, 3x – 2y = 3.
A14)
By changing the variables x, y to the new variables u and v, by the substitution x + y = u, 3x – 2y = v, the given parallelolgram R reduces to a rectangle 


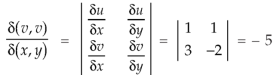
The required Jacobian is-

Since u = x + y and u = x + y = 2, here u varies from 0 to 2 while v varies from 0 to 3.
Since-
3x – 2y = v = 0, 3x – 2y = v = 3
Therefore the integral will be in new variables-

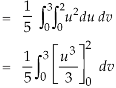

Q15) Evaluate 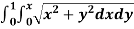 the transformation is x = v and y = uv.
the transformation is x = v and y = uv.
A15)
Here the region of integration R is the triangle which is bounded by y = 0, x = 1 and y = x
Here put,
X = u and y = uv, we get-


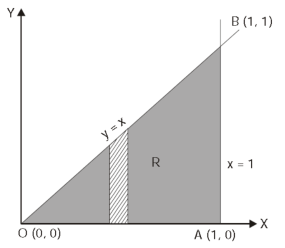
Here x varies from 0 to 1 while y varies from 0 to x.
Since u = x so u varies from 0 to 1
Here, similarly, since 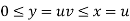 , so that v varies from 0 to 1. Thus-
, so that v varies from 0 to 1. Thus-


Q16) Evaluate-
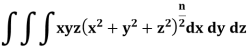
Taken through the positive octant of the sphere 
A16)
Since the geometry involves sphere, introduce spherical coordinates by x = 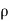 sin
sin  cos
cos 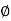 , y =
, y =  sin
sin  sin
sin  , z =
, z = 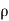 cos
cos  and the jacobian
and the jacobian
We get