Unit - 4

Sampling distributions

Q1) What do you understand by SRSWOR & SRSWR?

A1)
Simple Random Sampling without Replacement (SRSWOR)

In simple random sampling, if the elements or units are selected or drawn one by one in such a way that an element or unit drawn at a time is not replaced back to the population before the subsequent draws is called SRSWOR.

Suppose we draw a sample from a population, the size of sample is n and the size of population is N, then total number of possible sample is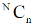

Simple Random Sampling with Replacement (SRSWR)

In simple random sampling, if the elements or units are selected or drawn one by one in such a way that a unit drawn at a time is replaced back to the population before the subsequent draw is called SRSWR.

Suppose we draw a sample from a population, the size of sample is n and the size of population is N, then total number of possible sample is .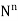

Q2) What is Sample mean and sample variance?

A2)

Let be a random sample of size n taken from a population whose pmf or pdf function f(x,

Then the sample mean is defined by-

And sample variance-

Q3) What do you understand by hypothesis?

A3)

A hypothesis is a statement or a claim or an assumption about the value of a population parameter.

Similarly, in case of two or more populations a hypothesis is comparative statement or a claim or an assumption about the values of population parameters.

For example-

If a customer of a car wants to test whether the claim of car of a certain brand gives the average of 30km/hr is true or false.

Simple and composite hypotheses-

If a hypothesis specifies only one value or exact value of the population parameter then it is known as simple hypothesis. And if a hypothesis specifies not just one value but a range of values that the population parameter may assume is called a composite hypothesis.

Null and alternative hypothesis

The hypothesis which is to be tested as called the null hypothesis.

The hypothesis which complements to the null hypothesis is called alternative hypothesis.

In the example of car, the claim is and its complement is .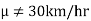

The null and alternative hypothesis can be formulated as-

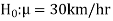
And

Q4) Define critical region.

A4)

Let be a random sample drawn from a population having unknown population parameter .

The collection of all possible values of is called sample space and a particular value represent a point in that space.

In order to test a hypothesis, the entire sample space is partitioned into two disjoint sub-spaces, say, and S – 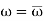. If calculated value of the test statistic lies in , then we reject the null hypothesis and if it lies in 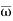then we do not reject the null hypothesis. The region is called a “rejection region or critical region” and the region is called a “non-rejection region”.

Therefore, we can say that

“A region in the sample space in which if the calculated value of the test statistic lies, we reject the null hypothesis then it is called critical region or rejection region.”

The region of rejection is called critical region.

The critical region lies in one or two tails on the probability curve of sampling distribution of the test statistic it depends on the alternative hypothesis.

Therefore there are three cases-

CASE-1: if the alternative hypothesis is right sided such as 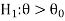then the entire critical region of size lies on right tail of the probability curve.

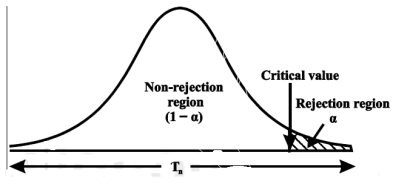
CASE-2: if the alternative hypothesis is left sided such as then the entire critical region of size lies on left tail of the probability curve.

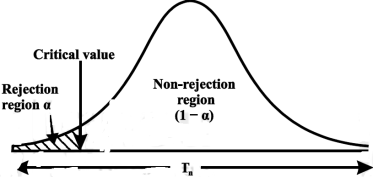
CASE-3: if the alternative hypothesis is two sided such as then the entire critical region of size 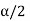lies on both tail of the probability curve

Q5) What are one-tailed and two tailed tests?

A5)

One tailed and two tailed tests-

A test of testing the null hypothesis is said to be two-tailed test if the alternative hypothesis is two-tailed whereas if the alternative hypothesis is one-tailed then a test of testing the null hypothesis is said to be one-tailed test.

For example, if our null and alternative hypothesis are-

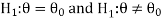
Then the test for testing the null hypothesis is two-tailed test because the

Alternative hypothesis is two-tailed.

If the null and alternative hypotheses are-

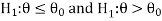
Then the test for testing the null hypothesis is right-tailed test because the alternative hypothesis is right-tailed.

Similarly, if the null and alternative hypotheses are-

Then the test for testing the null hypothesis is left-tailed test because the alternative hypothesis is left-tailed

Q6) A company of pens claims that a certain pen manufactured by him has a mean writing-life at least 460 A-4 size pages. A purchasing agent selects a sample of 100 pens and put them on the test. The mean writing-life of the sample found 453 A-4 size pages with standard deviation 25 A-4 size pages. Should the purchasing agent reject the manufacturer’s claim at 1% level of significance?

A6)

It is given that-

Specified value of population mean = 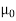= 460,

Sample size = 100

Sample mean = 453

Sample standard deviation = S = 25

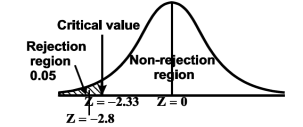
The null and alternative hypothesis will be-

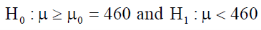
Also the alternative hypothesis left-tailed so that the test is left tailed test.

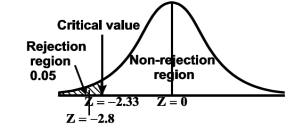
Here, we want to test the hypothesis regarding population mean when population SD is unknown. So we should used t-test for if writing-life of pen follows normal distribution. But it is not the case. Since sample size is n = 100 (n > 30) large so we go for Z-test. The test statistic of Z-test is given by

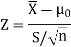
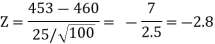
We get the critical value of left tailed Z test at 1% level of significance is

Since calculated value of test statistic Z (= ‒2.8) is less than the critical value

(= −2.33), that means calculated value of test statistic Z lies in rejection region so we reject the null hypothesis. Since the null hypothesis is the claim so we reject the manufacturer’s claim at 1% level of significance.

Q7) A manufacturer of electric bulbs claims that a certain pen manufactured by him has a mean life of at least 460 days. A purchasing officer selects a sample of 100 bulbs and put them on the test. The mean life of the sample found 453 days with a standard deviation of 25 days. Should the purchasing officer reject the manufacturer’s claim at a 1% level of significance?

A7)

Here the population mean =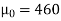

Sample size = n = 100

Sample mean =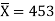

Sample standard deviation = S = 25

The null and alternative hypotheses will be-

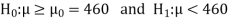
Here alternative hypothesis is left tailed so that the test is left tailed test-

Here population standard deviation is unknown so that we should use a t-test if the life of the bulbs follows a normal distribution.

But it is not the case. Here sample size is 100 which is large.

Note- a sample size of more than 30 is considered a large sample.

So here we use Z-test-

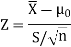
The critical value of Z statistic at a 1% level of significance is = -2.33

Since the calculated value of the test statistic is less than the critical value that means the test statistic lies in the rejection region.

Therefore we reject the null hypothesis.

So that we reject the manufacturer’s claim at a 1% level of significance.

Q8) What is CLT?

A8)

Whenever n is large, the sampling distribution of X is approximately (nearly) normal with mean μ and variance /n regardless of the form of the population distribution.

Theorem: If X is the mean of a sample of size n drawn from a population with mean μ and finite variance then the standardized sample mean

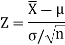
Is a random variable whose distribution function approaches that of the standard normal distribution N (Z; 0, 1) as n

Normal Population (Small Sample)- Sampling distribution of X is normally distributed even for small samples of size n < 30 provided sampling is from normal population.

Q9) A company of pens claims that a certain pen manufactured by him has a mean writing-life at least 460 A-4 size pages. A purchasing agent selects a sample of 100 pens and put them on the test. The mean writing-life of the sample found 453 A-4 size pages with standard deviation 25 A-4 size pages. Should the purchasing agent reject the manufacturer’s claim at 1% level of significance?

A9)

It is given that-

Specified value of population mean = = 460,

Sample size = 100

Sample mean = 453

Sample standard deviation = S = 25

The null and alternative hypothesis will be-

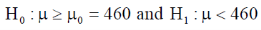
Also the alternative hypothesis left-tailed so that the test is left tailed test.

Here, we want to test the hypothesis regarding population mean when population SD is unknown. So we should used t-test for if writing-life of pen follows normal distribution. But it is not the case. Since sample size is n = 100 (n > 30) large so we go for Z-test. The test statistic of Z-test is given by

We get the critical value of left tailed Z test at 1% level of significance is

Since calculated value of test statistic Z (= ‒2.8) is less than the critical value

(= −2.33), that means calculated value of test statistic Z lies in rejection region so we reject the null hypothesis. Since the null hypothesis is the claim so we reject the manufacturer’s claim at 1% level of significance.

Q10) Eleven students were given a test in statistics. They were given a month’s further tuition and the second test of equal difficulty was held at the end of this. Do the marks give evidence that the students have benefitted by extra coaching?

A10)

We compute the mean and the S.D. Of the difference between the marks of the two tests as under:

Assuming that the students have not been benefitted by extra coaching, it implies that the mean of the difference between the marks of the two tests is zero i.e.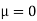

Then, nearly and df v=11-1=10

Students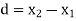
1	23	24	1	0	0
2	20	19	-1	-2	4
3	19	22	3	2	4
4	21	18	-3	-4	16
5	18	20	2	1	1
6	20	22	2	1	1
7	18	20	2	1	1
8	17	20	3	2	4
9	23	23	-	-1	1
10	16	20	4	3	9
11	19	17	-2	-3	9

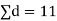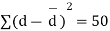We find that 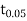(for v=10) =2.228. As the calculated value of 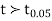, the value of t is not significant at 5% level of significance i.e. the test provides no evidence that the students have benefitted by extra coaching.

Q11) A college conducts both face to face and distance mode classes for a particular course indented both to be identical. A sample of 50 students of face to face mode yields examination results mean and SD respectively as-

And other sample of 100 distance-mode students yields mean and SD of their examination results in the same course respectively as:

Are both educational methods statistically equal at 5% level?

A11)

Here we have-

Here we wish to test that both educational methods are statistically equal. If denote the average marks of face to face and distance mode students respectively then our claim is and its complement is ≠ . Since the claim contains the equality sign so we can take the claim as the null hypothesis and complement as the alternative hypothesis. Thus,

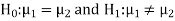
Since the alternative hypothesis is two-tailed so the test is two-tailed test.

We want to test the null hypothesis regarding two population means when standard deviations of both populations are unknown. So we should go for t-test if population of difference is known to be normal. But it is not the case.

Since sample sizes are large (n1, and n2 > 30) so we go for Z-test.

For testing the null hypothesis, the test statistic Z is given by

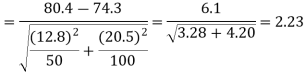
The critical (tabulated) values for two-tailed test at 5% level of significance are-

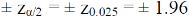
Since calculated value of Z ( = 2.23) is greater than the critical values

(= ±1.96), that means it lies in rejection region so we

Reject the null hypothesis i.e. we reject the claim at 5% level of significance

Q12) A tube manufacturer claims that the average life of a particular category

Of his tube is 18000 km when used under normal driving conditions. A random sample of 16 tube was tested. The mean and SD of life of the tube in the sample were 20000 km and 6000 km respectively.

Assuming that the life of the tube is normally distributed, test the claim of the manufacturer at 1% level of significance using appropriate test.

A12)

Here we have-

We want to test that manufacturer’s claim is true that the average life (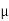) of tube is 18000 km. So claim is μ = 18000 and its complement is μ ≠ 18000. Since the claim contains the equality sign so we can take the claim as the null hypothesis and complement as the alternative hypothesis. Thus,

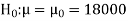
Here, population SD is unknown and population under study is given to be normal.

So here can use t-test-

For testing the null hypothesis, the test statistic t is given by-

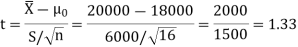
The critical value of test statistic t for two-tailed test corresponding (n-1) = 15 df at 1% level of significance are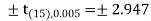

Since calculated value of test statistic t (= 1.33) is less than the critical (tabulated) value (= 2.947) and greater that critical value (= − 2.947), that means calculated value of test statistic lies in non-rejection region, so we do not reject the null hypothesis. We conclude that sample fails to provide sufficient evidence against the claim so we may assume that manufacturer’s claim is true.

Q13) Two sources of raw materials are under consideration by a bulb manufacturing company. Both sources seem to have similar characteristics but the company is not sure about their respective uniformity. A sample of 12 lots from source A yields a variance of 125 and a sample of 10 lots from source B yields a variance of 112. Is it likely that the variance of source A significantly differs to the variance of source B at significance level  α = 0.01?

A13)

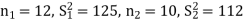
The null and alternative hypothesis will be-

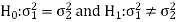
Since the alternative hypothesis is two-tailed so the test is two-tailed test.

Here, we want to test the hypothesis about two population variances and sample sizes 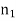= 12(< 30) and = 10 (< 30) are small. Also populations under study are normal and both samples are independent.

So we can go for F-test for two population variances.

Test statistic is-

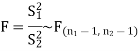
The critical (tabulated) value of test statistic F for two-tailed test corresponding 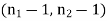= (11, 9) df at 5% level of significance are 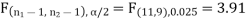and

Since calculated value of test statistic (= 1.11) is less than the critical value (= 3.91) and greater than the critical value (= 0.28), that means calculated value of test statistic lies in non-rejection region, so we do not reject the null hypothesis and reject the alternative hypothesis. We conclude that samples provide us sufficient evidence against the claim so we may assume that the variances of source A and B is differ.

Q14) A set of five similar coins is tossed 320 times and the result is

A14)

For v = 5, we have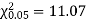

P, probability of getting a head=1/2;q, probability of getting a tail=1/2.

Hence the theoretical frequencies of getting 0,1,2,3,4,5 heads are the successive terms of the binomial expansion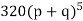

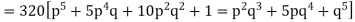
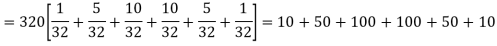
Thus the theoretical frequencies are 10, 50, 100, 100, 50, 10.

Hence,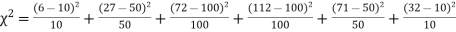

Since the calculated value of 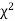is much greater than 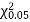the hypothesis that the data follow the binomial law is rejected.

Q15) In experiments of pea breeding, the following frequencies of seeds were obtained

Theory predicts that the frequencies should be in proportions 9:3:3:1. Examine the correspondence between theory and experiment.

A15)

The corresponding frequencies are

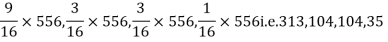
Hence,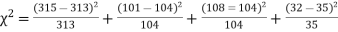

For v = 3, we have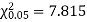

Since the calculated value of 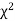is much less than 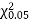there is a very high degree of agreement between theory and experiment.

Q16) What do you understand by correlation?

A16)

So far we have confined our attention to the analysis of observations on a single variable. There are however, many phenomenon where the changes in one variable are related to the changes in the other variable. For instance the yield of a crop varies with the amount of rainfall, the price of a commodity increases with the reduction in its supply and so on. Such a data connecting two variables is called bivariate population.

To obtain a measure of relationship between the two variables, we plot their corresponding values on the graph taking one of the variable along the x axis and the other along the y axis. (Figure 25.6).

Let the origin be shifted to 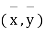, where 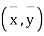re the means of X’s and y's that the new coordinates are given by

Now the points (X,Y) are so distributed over the four quadrants of XY plane that the product XY is positive in the first and third quadrant but negative in the second and fourth quadrants. The algebraic sum of the products can be taken as describing the trend of the dots in all the quadrants.

(i)                If XY is positive, the trend of the dots is through the first and third quadrants.

(ii)              If 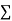XY is negative the trend of two dots is in the second and fourth quadrants and

(iii)           If XY is zero, the points indicate no trend i.e. the points are evenly distributed over the quadrants.

The 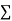XY or better still 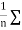XY i.e. the average of n products may be taken as a measure of correlation. If we put X and Y in their units, i.e. taking, as the unit for x and 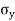for y, then

Is the measure of correlation.

Coefficient of correlation

The numerical measure of correlation is called the coefficient of correlation and is defined by the relation

Where, X = deviation from the mean = = devaluation from the mean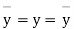

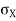= Standard deviation of x series, 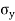= standard deviation of y series and n = number of the values of the two variables

Q17) Psychological test of the intelligence and of Engineering ability were applied to 10 students. Here is a record of ungrouped data showing intelligence ratio (I.R) and Engineering ratio (E.R). Calculate the coefficient of correlation.

A17)

We construct the following table

Student	Intelligence ratio x	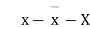Engineering ratio y y	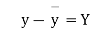		XY
A	105             6	101               3	36	9	18
B	104             5	103                5	25	25	25
C	102             3	100                2	9	4	6
D	101             2	98                  0	4	0	0
E	100             1	95                 -3	1	9	-3
F	99               0	96                - 2	0	4	0
G	98               -1	104                 6	1	36	-6
H	96              -3	92                   -6	9	36	18
I	93             -6	97                  -1	36	1	6
J	92              -7	94                  -4	49	16	28
Total	990             0	980                  0	170	140	92

From this table, mean of x, i.e. 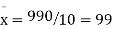and mean of y, i.e.

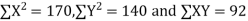
Substituting these value in the formula (1)p.744 we have

Q18) The two regression equations of the variable x and y are x = 19.13 and y = 11.64 – 0.50 x. Find (i) mean of x’s (ii) mean of y’s and (iii) the correlation coefficient between x and y.

A18)

Since the mean of x’s and the mean of y’s lie on the two regression lines, we have

Multiplying (ii) by 0.87 and subtracting from (i) we have

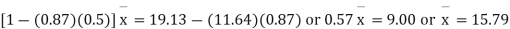
Regression coefficient of y and x is -0.50 and that of x and y is -0.87.

Now since the coefficient of correlation is the geometric mean between the two regression coefficients.

[-ve sign is taken since both the regression coefficients are –ve]

Q19) If is the angle between the two regression lines show that

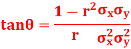
Explain the significance when

A19)

The equations to the line of regression of y on x and x on y are

Their slopes are

Thus,

When  r = 0,i.e. when the variable are independent, the two lines of regression are perpendicular to each other.

When . Thus the line of regression coincide i.e. there is perfect correlationbetween the two variables.

Q20) Three judges A,B,C give the following ranks. Find which pair of judges has common approach

A20)

Here n = 10

A (=x)	Ranks by B(=y)	C (=z)	x-y	y - z	z-x
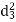1	3	6	-2	-3	5	4	9	25
6	5	4	1	1	-2	1	1	4
5	8	9	-3	-1	4	9	1	16
10	4	8	6	-4	-2	36	16	4
3	7	1	-4	6	-2	16	36	4
2	10	2	-8	8	0	64	64	0
4	2	3	2	-1	-1	4	1	1
9	1	10	8	-9	1	64	81	1
7	6	5	1	1	-2	1	1	4
8	9	7	-1	2	-1	1	4	1
Total			0	0	0	200	214	60

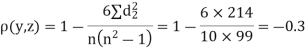
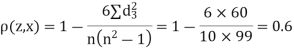
Since 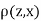is maximum, the pair of judge A and C have the nearest common approach.

Q21) Find the best values of a and b so that y = a + bx fits the data given in the table

A21)

y = a + bx

x	y	Xy
0	1.0	0	0
1	2.9	2.0	1
2	4.8	9.6	4
3	6.7	20.1	9
4	8.6	13.4	16
x = 10	y ,= 24.0	xy = 67.0

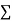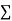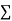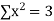Normal equations, 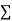y= na+ b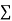x  (2)

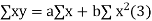
On putting the values of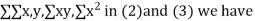

On solving (4) and (5) we get,

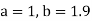
On substituting the values of a and b in (1) we get

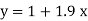
Q22) Fit a second degree parabola to the following data.

A22)

We shift the origin to (2.5, 0) antique 0.5 as the new unit. This amounts to changing the variable x to X, by the relation X = 2x – 5.

Let the parabola of fit be y = a + bX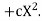 The values of X etc. Are calculated as below:

x	X	y	Xy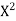
1.0	-3	1.1	-3.3	9	9.9	-27	81
1.5	-2	1.3	-2.6	4	5.2	-5	16
2.0	-1	1.6	-1.6	1	1.6	-1	1
2.5	0	2.0	0.0	0	0.0	0	0
3.0	1	2.7	2.7	1	2.7	1	1
3.5	2	3.4	6.8	4	13.6	8	16
4.0	3	4.1	12.3	9	36.9	27	81
Total	0	16.2	14.3	28	69.9	0	196

The normal equations are

7a + 28c =16.2; 28b =14.3;. 28a +196c=69.9

Solving these as simultaneous equations we get

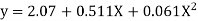
Replacing X bye 2x – 5 in the above equation we get

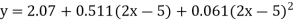
Which simplifies to y =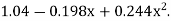 This is the required parabola of the best fit