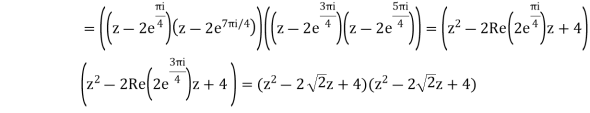Unit - 2

Cauchy’s Theorem and Its Applications

Q1) Explain Cauchy’s theorem with Simply-connected regions.

A1)

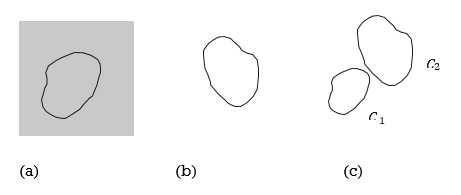
If any closed curve in an area can be shortened to a point without any part of it leaving the region, it is said to be simply connected. Simply connected regions include the inside of a square or a circle. The dark grey area in Figure (a) and (b) is the region, and a typical closed curve is depicted inside the region. Figure (c) shows a region with a hole (the white area inside). Because of the hole inside the shaded region between the two circles, curve C1 can shrink to a point, but curve C2 cannot shrink to a point without leaving the region.

As an example, consider the following: 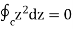Since z2 is analytic everywhere, C is the unit circle. Indeed    Any basic contour does not have to be round.

Assume that f(z) is analytic everywhere on and inside the contour C, as shown in Figure below.

Then, using real line integrals as an analogy,

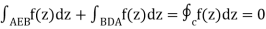by Cauchy’s theorem

Therefore

(Because reversing the direction of integration changes the integral's sign.)

This means that if f(z) is analytic in the region in question, we can take any path between A and B and the integral will have the same result.

The placements of the points A and B, not the path connecting them, determine the integrals of analytic functions. This explains the previously mentioned "coincidences" in Section 26.4.

Evaluate using a ‘simple' integration method. 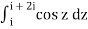, and justify your position.

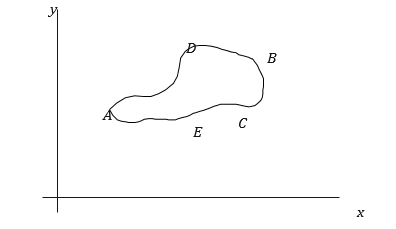
Now we'll look at what happens when the closed path of integration isn't always found within a simple-connected region. Take a look at the situation depicted in Figure.

Graph

In the region bounded by the closed curves C1 and C2, let f(z) be analytic. The line section connecting A and B cuts through the region.

Take a look at the closed curve AEABFBA moving in the direction indicated by the arrows. No line can cross the cut AB and still be considered a part of the region. The shaded portion is simply connected due to the cut. As a result, Cauchy's theorem is applicable.

Therefore

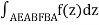 because f(z) is analytic within and on the AEABFBA curve

Keep in mind that

It's just a simple change of pace.

We can also break the closed curve down into smaller sections:

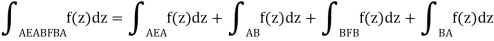
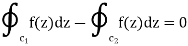
(since we assume that closed paths are travelled anticlockwise).

Therefore

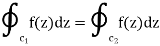
This permits us to assess the situation. 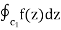by substituting C1 with any curve C2 that has no singularities in the region between them (see Section 261) of f (z). C2 is frequently chosen as a circle.

Q2) Explain Cauchy’s integral formula with two example each.

A2)

Cauchy's theorem is a big theorem that we'll be using virtually every day from now on. It will immediately expose a variety of useful and fascinating properties of analytic functions. As the course proceeds, more will be added.

We begin with a statement of the function theorem. We'll give a generalisation to all derivatives of a function after various examples. We'll prove the theorems after some additional cases. Following that, we'll see some striking results that come quite directly from Cauchy's formula.

Cauchy’s integral for functions

Theorem. (The integral formula of Cauchy) Suppose C is a simple closed curve and the function f(z) is analytic on a region containing C and its interior. We'll assume C is positioned in the other direction. Then, inside C, for any z0:

Cauchy's integral formula is as follows: simple closed curve C, analytic f(z) on and inside C.

This is amazing: it indicates that knowing the values of f on the boundary curve C means we know everything there is to know about f inside C!! This is probably unlike anything you've seen before with real-valued functions.

Aside 1. We commonly express the formula as with a small change of notation (z becomes w and z0 becomes z).

Aside 2. We aren't treating functions of real variables fairly. We'll see that the real and imaginary components u and v of f = u + iv have a lot of traits in common. Conjugate harmonic functions are u and v.

Examples

Example. Compute 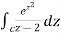 , where C is the curve shown.

Solution: Let f(z) = ez2. f(z) is entire. Since C is a simple closed curve ( counter clockwise ) and z = 2 is inside C, Cauchy’s integral formula says that the integral is 2πif(2) = 2πie4.

Q3) Explain Cauchy’s integral formula for derivatives with two examples.

A3)

It's worth repeating Cauchy's integral formula multiple times. As a result, we now provide it for all derivatives.  f(n)(z) of f. As a special situation, the formula for functions will be included.

Theorem: For derivatives, Cauchy's integral formula is used. If the hypotheses for f(z) and C are the same as for Cauchy's integral formula, then we have for all z inside C.

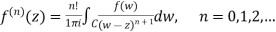  (3)

Where C is a simple counter clockwise closed curve, z is inside C, and f(w) is analytic on and inside C.

Example. Evaluate  where C: |z| = 1.

Solution: This is simple with Cauchy's derivatives formula. Let f(z) = e2z. Then,

Example. Let C represent the contour given below, and assess the same integral as before.

Solution: This is also straightforward: the integral is the same as in the preceding case, i.e.

Q4) State Goursat’s theorem and prove it.

A4)

Statement of the Theorem

The integral of a holomorphic function over a triangle in the complex plane is 0 +0i, according to the Cauchy-Goursat Theorem. (i.e. the integral's real and imaginary components both equal 0)

Proof

Step 1: four congurent triangles

By drawing lines linking the triangle's midpoints, we were able to divide it into four sections.

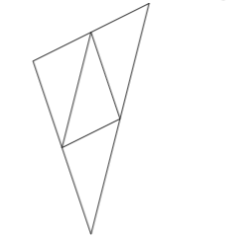
The perimeter of each of these new triangles is half that of the original triangle. The diameter is defined as the maximum distance between two points, which is also one half the original triangle's diameter. Because the four new triangles are congruent with the bigger one, this is the case.

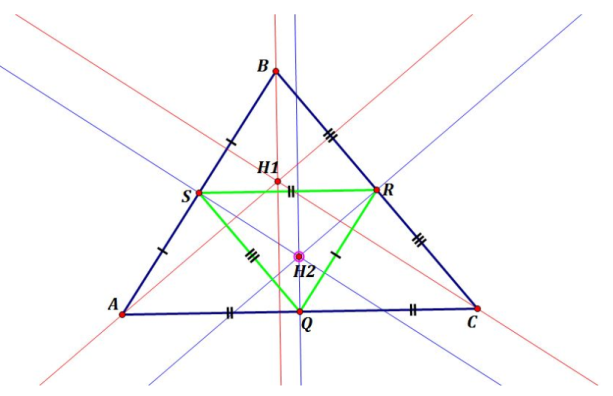
We now assert that the contours surrounding the four smaller triangles are the same as those surrounding the larger triangle.

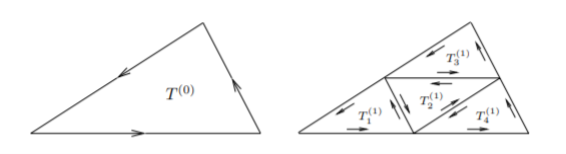
This can be seen in the image above. The arrows in opposite directions cancel out all of the paths on the inside, leaving only the path on the outside.

So, if T is the original triangle and T 1, T 2, T 3, T 4 are the four smaller triangles, we have the following equation.

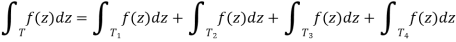
We get the following by using the triangle inequality (see the end of the previous section on requirements). T

The last inequality holds for some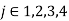

T j denotes the triangle with the biggest integral magnitude in the example above. (As a result, the sum of the magnitudes of all four triangles is 4 times the magnitude of the largest.) For example, if the magnitudes of the four triangles are 1,5, 3, and 2, then 1+5+3+2 = 5 + 5 + 5 + 5 = 4*5.

Step 2: iterating the first step

Now, we repeat this iteratively: we split the triangle T_j (which was the triangle whose integral had the largest magnitude) into four parts and repeat. We get after repeating this n times.

T*n denotes the nth triangle we chose. In essence, we repeated the initial method and discovered a new triangle embedded in the previous one we chose each time.

Because each of these triangles is nested inside the previous (and thus are ‘closed' sets in technical terms), it turns out that there is a point inside each of them. At this point, we employ holomorphism (the presence of the complex derivative). Close to the point, we can write a linear approximation, with the ‘gradient' term given by the derivative, much like in real calculus. That is exactly what we do down here.

where 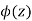tends to zero as .

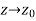[we can do this almost by definition of the derivative]. However, 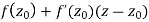both have primitives (anti-derivatives) so their integrals are zero.

We used holomorphism (the existence of the complex derivative) and the fact that the integral of a function with an anti-derivative around a closed curve equals 0 to solve this problem.

Step 3: some elementary bounds on the size of integral around the Nth triangle, and looking at the behaviour of these bounds as N gets arbitrarily large.

Now we're going to use our final trick. The size of the integral of f along a curve C is always less than the curve's length and the function's maximum magnitude at any point along the curve. For example, the maximum quantity of energy you burn when running is always less than the length of the route multiplied by your maximum energy burn rate. For the nth triangle, however, we know the length of the curve and the maximum distance between two points.

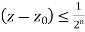and the length of 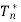is 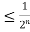, so we conclude

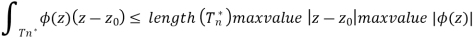
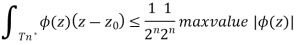
The final term decreases to 0 as n approaches infinity, as this was the error term of our expansion: as our triangle gets arbitrarily small, the approximation we made becomes arbitrarily good, and therefore the error term tends to 0. This leaves only one choice:

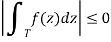
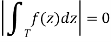
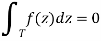
We previously said that the magnitude of a value can only be zero if there is no distance between it and the origin, and so it is 0.

Q5) What is local existence of primitives?

A5)

The antiderivative, or primal, of a complex-valued function in complex analysis, a branch of mathematics. g is the complex derivative of a function. More precisely, given an open set 𝑈 in the complex plane and a function g:U→C the antiderivative of f:U→C  is a function that satisfies  

As a result, this idea is the complex-variable version of a real-valued function's antiderivative.

Existence

Path integrals in the complex plane, like functions of a real variable, can be used to characterise the existence of antiderivatives. Perhaps unsurprisingly, g has an antiderivative f if and only if the path integral from a to b is positive.

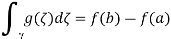
Equivalently,

For any path that is closed

Despite their formal similarities, having a complex-antiderivative is a far more restricted condition than having a genuine counterpart. While an anti-derivative can exist for a discontinuous real function, anti-derivatives can also fail to exist for holomorphic functions of a complex variable. Consider the reciprocal function g(z) = 1/z on the punctured plane C0, which is holomorphic. The integral of g along any circle encompassing the origin is non-zero, according to a direct calculation. As a result, g fails the above-mentioned criteria. Green's theorem, like the Cauchy integral theorem, can only guarantee path independence when the function is defined on a simply connected region.

In fact, holomorphy is defined as having an antiderivative locally, i.e., g is holomorphic if there is some neighbourhood U of z in its domain where g has an antiderivative on U. Furthermore, because the derivative of any holomorphic function is holomorphic, holomorphy is a necessary condition for a function to have an antiderivative.

Various variants of the Cauchy integral theorem, a foundational conclusion of Cauchy function theory that heavily relies on route integrals, provide adequate conditions for a holomorphic g to exist.

For any closed path, disappears (which may be, for instance, that the domain of g be simply connected or star-convex).

Q6) Explain Cauchy's Theorem for a disc with one example.

A6)

Theorem 

Let   be a disc, and let 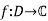  be holomorphic (i.e. complex-differentiable). Then for every closed curve  ,

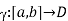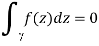This will be reduced to the analogous result for triangles using the fundamental theorem of calculus.

Definition 

If 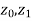,  are complex numbers we denote by  the curve

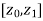Less formally,  is the line segment joining  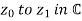 traversed from  .

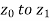Q7) Show Evaluation of some integrals with two examples.

A7)

Let's begin with a very basic example. It is simple to demonstrate that the widely used integral

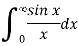
Is convergent is convergent is convergent is convergent. We introduce the function in order to assess this integral.

And distinguish this function in order to obtain

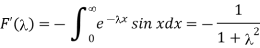
(The sine function's Laplace transform.) Returning to the beginning, we discover

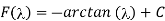
Setting λ→∞ yields the equation 

And therefore, 

Taking limits for λ→ 0 we find 

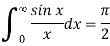
Q8) The integral was featured in the 66th Annual William Lowell Putnam Mathematical Competition.

A8)

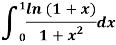
By introducing a parameter, we will provide a new solution. Consider the purpose.

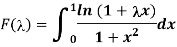
Defined for λ≥ 0.  Differentiating this function we get 

This integral is easy to evaluate by splitting the integrand in partial fractions. As a result,

We discover that integrating is beneficial.

And setting λ=1 we arrive at the equation 

That is, 

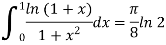
This approach can be used to evaluate numerous integrals incorporating logarithms and inverse trigonometric functions, as we'll see later.

It's worth noting that when we integrate (1.9) by parts, we find

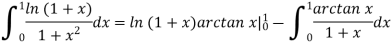
As a result, we've also

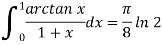
Q9) Evaluate

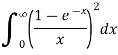
A9)

We show that for every λ> 0  

Indeed, differentiating this function with respect to λ (which is legitimate, as the integral is uniformly convergent on every interval 0 < a <λ< b) we find 

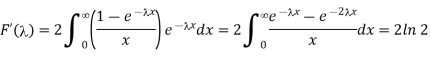
By using Frullani’s formula for the last equality (see below). 

We conclude that F(λ) is a linear function and since F(0) = 0 we can write F(λ) =λln 4. With λ=1 we find F(1) = ln 4 . 

Frullani’s formula says that for appropriate functions f (x) we have 

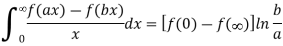
Q10) Write the following functions f(z) in the forms f(z) = u(x, y) +iv(x, y) under Cartesian coordinates with u(x, y) = Re(f(z)) and v(x, y) = Im(f(z)):

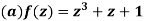
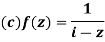
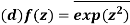
A10)

a-

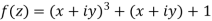
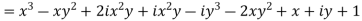
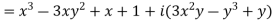
b-

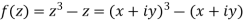
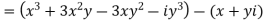
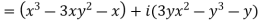
c-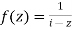

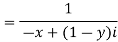
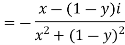
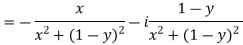
d-

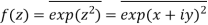
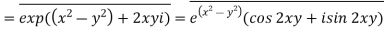
Q11) Define Integration along the curve.

A11)

Finding the slope of the tangent line to a graph y=f(x) is easy -- just compute f′(x). Likewise, the area under the curve between x=a and x=b is just 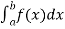 But how do we compute slopes and areas with parametrized curves?

The answer is to express everything in terms of the parameter t. By computing derivatives with respect to t and integrals with respect to t, we can compute everything we want.

For slopes, we are looking for dy/dx. This is a limit

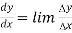
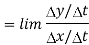
Where the limits are as Δt and Δx and Δy all go to zero. As long as we can take the derivatives of x and y, we can compute dy/dx.

Example: Find the slope of the tangent to the unit circle x=cos(t); y=sin(t) at time 

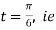at the point .

Solution:

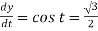and

To find the area under a curve between x=a and x=b, we need to compute

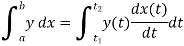
Where x(t1)=a and x(t2)=b. To find the area, we need to both compute a derivative as well as an integral.

Q12) Find all complex solutions of the following equations:

(a) z = z;

(b) z+z = 0;

(c) z = 9 z

A12)

(a) Let z = z+iy.

Thus z = z x+iy = x+iy x−iy = x+iy −iy = iy y = 0

Hence, z = z if and only if Imz = 0.

(b) Let z = z+iy.

Thus z+z = 0 x+iy+z+iy

= 0 x−iy+x+iy

= 0 2x

= 0 x

= 0

Hence, z+z if and only if Rez = 0.

(c) In this part we have,

z = 9 z ⇐⇒ zz = 9 ⇐⇒ |z| 2 = 9 ⇐⇒ |z| = 3.

Hence, z = 9 z if and only if |z| = 3. 

Q13) Suppose that z1 and z2 are complex numbers, with z1z2 real and non-zero. Show that there exists a real number r such that z1 = rz2.

A13)

Let z1 = x1 +iy1 and z2 = x2 +iy2 with x1, x2, y1, y2 ∈ R.

Thus z1z2 = x1x2 −y1y2 + (x1y2 +y1x2)i

Since z1z2 is real and non-zero, z1 6= 0, z2 6= 0, and x1x2 −y1y2 6= 0 and x1y2 +y1x2 = 0.

Thus,

Since z2 6= 0,

Then z1 z2 = x1 +iy1 x2 −iy2 · x2 +iy2 x2 +iy2

= x1x2 −y1y2 + (x1y2 +y1x2)i x 2 2 +y 2 2

= x1x2 −y1y2 x 2 2 +y 2 2.

By setting r = x1x2 −y1y2 x 2 2 +y 2 2,

We have the result.

Q14) Solve the following

(A) Use exponential form to compute (i) (1+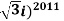  (ii) (1+

(B) Prove that

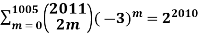and

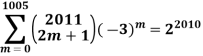
A14)

We have

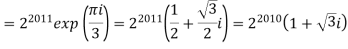
Similarly,

By problem 7 in section 1.1 we have

It follows that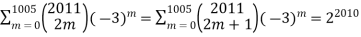

Q15) Use complex numbers to prove the Law of Cosine: Let ∆ABC be a triangle with |BC| = a, |CA| = b, |AB| = c and ∠BCA = θ.

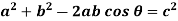
Hint: Place C at the origin, B at z1 and A at z2. Prove that z1z2 +z2z1 = 2|z1z2| cosθ

A15)

Following the hint, we let C = 0, B = z1 and A = z2.

Then a = |z1|, b = |z2| and c = |z2 −z1|.

So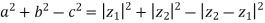

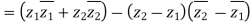
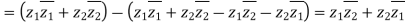
Let and . Then

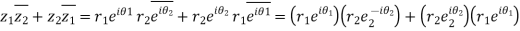
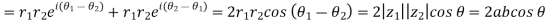
Therefore, we have

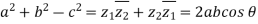
And hence

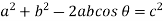
Q16) Establish the identity

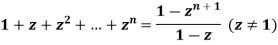
And then use it to derive Lagrange’s trigonometric identity

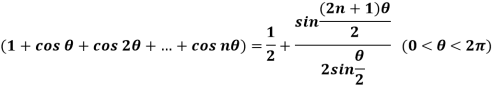
Hint: As for the first identity write 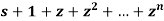and consider the difference 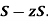To derive the second identity write in the first one.

A16)

If 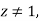then

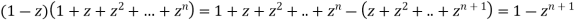
Thus

Taking 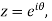where then 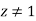. Thus

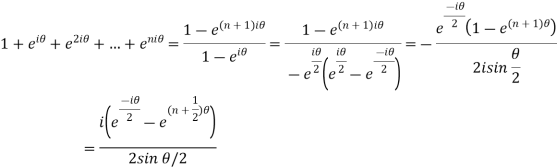
Q17) Express the following in the form x+iy, with x, y ∈ R:

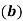all the 3rd roots of -8i

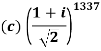
A17)

a-

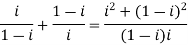
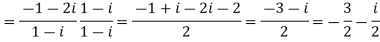
b-

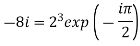
Thus the cube roots are

and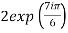

That is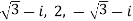

c-

Q18) Find the principal argument and exponential form of-

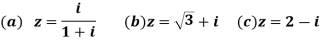
A18)

(a)

(b)

(c)

Q19) Find all the complex roots of the equations:

A19)

(a) The roots are-

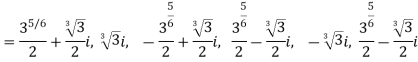
(b) The roots are

Q20) Find the four roots of the polynomial

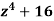and use these to factor 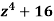into two quadratic polynomials with real coefficients.

A20)

The four roots of 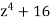are given by

For m=0,1,2,3. We see that these roots appear in conjugate pairs

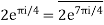and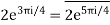

This gives the way to factor 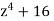into two quadratic polynomials of real coefficients