Unit - 2
Commutator subgroup and its properties
Q1) Let x,y,z∈G be elements of a group G then
Prove: (xy,z) = (x,z)y(y,z) = (x,z)(x,z,y)(y,z)
A1)
Consider, (xy,z) = (xy)-1z-1(xy)z = y-1x-1z-1xyz
Consider, (x,z)y(y,z) = y-1(x,z)y(y,z)
= y-1x-1z-1xzyy-1z-1yz
= y-1x-1z-1xyz
Again, (x,z)(x,z,y)(y,z)
= x-1z-1xz(x,z)-1y-1(x,z)yy-1z-1yz
= x-1z-1xzz-1x-1zxy-1x-1z-1xzyy-1z-1yz
= y-1x-1z-1xyz
Hence, (xy,z) = (x,z)y(y,z) = (x,z)(x,z,y)(y,z)
Q2) Let x,y,z be elements of a group G. Then
Prove: (x,yz)=(x,z)(x,y)z=(x,z)(x,y)(x,y,z)
A2)
Consider, (x,yz) = x-1(yz)-1xyz = x-1z-1y-1xyz
Consider, (x,z)(x,y)z = (x,z)z-1(x,y)z
= x-1z-1xzz-1x-1y-1xyz
= x-1z-1y-1xyz
Again (x,z)(x,y)(x,y,z) = x-1z-1xzx-1y-1xyx-1(y,z)-1x(y,z)
=x-1z-1xzx-1y-1xyy-1x-1yxz-1x-1y-1xyz
= x-1z-1y-1xyz
Hence, (x,yz) = (x,z)(x,y)z = (x,z)(x,y)(x,y,z)
Q3) Let x,y,z be elements of a group G, Then
Prove: (x,y-1,z)y(y,z-1,x)z(z,x-1,y)x = e, the identity of G
A3)
Consider (x,y-1,z)y = y-1(x,y-1,z)y
= y-1(x,y-1)-1z-1(x,y-1)zy
= y-1yx-1yxz-1x-1yxy-1zy
= x-1yxz-1x-1y xy-1zy (a)
Similarly, (y,z-1,x)z = z-1(y,z-1,x)z
= z-1(y,z-1)-1x-1(y,z-1)xz
= z-1zy-1z-1yx-1y-1zyz-1xz
=y-1z-1yx-1y-1zyz-1xz (b) Again,
(z,x-1,y)x = x-1(z,x-1,y)x
= x-1(z,x-1)-1y-1(z,x-1)yx
= x-1xz-1x-1zy-1z-1xzx-1yx
=z-1x-1zy-1z-1xzx-1yx (c)
Now, Combining (a),(b),(c), we get
x-1y-1xz-1x-1yxy-1zy y-1z-1yx-1y-1zyz-1xz z-1x-1zy-1z-1xzx-1yx =e(identity)
Hence, (x,y-1,z)y(y,z-1,x)z(z,x-1,y)x = e, the identity of G.
Q4) Let x,y,z be elements of a group G, then
Prove: (x,y,z)(y,z,x)(z,x,y)=(y,x)(z,x)(z,y)x(x,y)(x,z)y(y,z)x(x,z)(z,x)y
A4)
L.H.S. (x,y,z)(y,z,x)(z,x,y)
= (x,y)-1z-1(x,y)z(y,z)-1x-1(y,z)x(z,x)-1y-1(z,x)y
= y-1x-1yxz-1x-1y-1xyzz-1y-1zyx-1y-1z-1yzxx-1z-1xzy-1z-1x-1zxy
= y-1x-1yxz-1x-1y-1xzyx-1y-1z-1yxzy-1z-1x-1zxy
R.H.S. (y,x)(z,x)(z,y)x(x,y)(x,z)y(y,z)x(x,z)(z,x)y
= (y,x)(z,x)x-1(z,y)x(x,y)y-1(x,z)yx-1(y,z)x(x,z)y-1(z,x)y
= y-1x-1yxz-1x-1zxx-1z-1y-1zyxx-1y-1xyy-1x-1z-1xzyx-1y-1z-1yzxx-1z-1xzy-1z-1x-1zxy
= y-1x-1yxz-1x-1y-1xzyx-1y-1z-1yxzy-1z-1x-1zxy
Therefore, L.H.S. = R.H.S
Q5) Let x,y,z be elements of a group G, then
Prove (x,y,z) = ((z,x-1,y-1)xy)-1((y-1,z-1,x)zy)-1
A5)
L.H.S (x,y,z) = (x,y)-1z-1(x,y)z
= y-1x-1yxz-1 x-1y-1xyz
R.H.S. ((z,x-1,y-1)xy)-1 = [(xy)-1(z,x-1,y-1)xy)]-1
= [y-1x-1(z,x-1)-1(y-1)-1(z,x-1)y-1xy]-1
= (y-1x-1xz-1x-1zyz-1xzx-1y-1xy)-1
= y-1x-1yxz-1x-1zy-1z-1xzx-1xy
=y-1x-1yxz-1x-1zy-1z-1xzy (a)
Again,
((y-1,z-1,x)zy)-1 = [(zy)-1(y-1,z-1,x)zy]-1
= [y-1z-1(y-1,z-1)-1x-1(y-1,z-1)xzy]-1
= [y-1z-1zyz-1y-1x-1 yzy-1z-1xzy]-1
= [z-1y-1x-1 yzy-1z-1xzy]-1
= y-1z-1x-1zyz-1y-1xyz (b)
Combining (a) and (b) we get
y-1x-1yxz-1x-1zy-1z-1xzyy-1z-1x-1zyz-1y-1xyz = y-1x-1yxz-1x-1y-1xyz
Hence, L.H.S=R.H.S and the proof follows:
Q6) Let x,y,z be element of a group G then
Prove:
(i) If is commutes with z and if (x,G) is abelian then
(x,y,z)=(x,z,y)
(ii) If (x,y) commutes with both x and y then
(xy-1)-1=(x-1,y)=(x,y-1)
A6)
First (x,y,z ) = (x,y)-1z-1(x,y)(z)
= y-1x-1yxz-1x-1y-1xyz
= x-1(xy-1x-1y)(xz-1x-1z)(z-1y-1xyz)
Furthermore, xy-1xy = (x-1,y) = (xm,y) for some positive integer m, we conclude easily by p-2 that (xm,y)∈(x,G) .
Thus, xy-1x-1y, and likewise xz-1x-1z lies in (x,G).
Hence, by hypothesis these two elements commute. It follows, therefore, that
(x,y,z) = x-1(xy-1x-1y)(xz-1x-1z)(z-1y-1xyz)
Since, y and z commute by assumption, this reduces to
(x,y,z) = z-1x-1zxy-1x-1z-1xzy
= (x,z,y)
Which proves (i)
We have, e = (xx-1,y )= (x,y)(x,y,x-1)(x-1,y)
But, (x,y,x-1) = ((x,y),x-1) and (x,y) commute with x by hypothesis, whence (x,y,x-1) = e
Hence, e = (x,y)(x-1,y) and consequently, (x,y)-1 = (x-1,y)
Similarly, by p-3, we obtain(x,y)-1 = (x,y-1) by (i ) holds
Q7) Explain the Commutator Subgroup?
A7)
Let G stand for any group. If a, b G, then the element aba1 b 1 is the commutator of a and b. Naturally, if a and b commute, aba1 b 1 = e. Define C as the set C = x1x2 •••xn | n 1 | n I where xi is a commutator in G.
In other words, C is the set of all finite commutator products in G. After that, there's Proposition 1. If G is any group, then C C G is the answer. Proof. First, we have e = eee1 e 1 C, and then we have e = eee1 e 1 C.
As a result, C is nonempty and holds the identity
If c, d are both C, we get c = x1x2 •••xn and d = y1y2 •••ym, with each xi and yj being a commutator in G.
Cd = x1x2 ••• xny1y2 •••ym C, then
Since this is just another finite commutator product
We also have d −1 = (x1x2 ···xn) −1 = x −1 n ··· x −1 2 x −1 1 .
If xi = aibia−1 i b −1 i , then x −1 i = biaib−1 i a −1 i ,
Which is also a commutator.
Q8) Let x,y be elements of a group G and suppose that z = (x,y) commutes with both x and y
Then prove: (i)(xi,yj) = zij for all j
(ii) 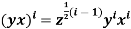 for all I
for all I
A8)
Since x-1y-1xy = z, then we have y-1xy = xz where y-1xiy = (y-1xy)i = (xz)i = xizi as x and z commute. Conjugating by y which gives that
y-1(y-1xiy)y = y-1 (xizi)y = (xizi)zi = xiz2i
As y and z commute.
Repeating this argument j times. We conclude that
y-jxiyj = xizij and (xi,yj) = zij
Again, (ii) holds, for j=1, assuming the result for (i-1), we have
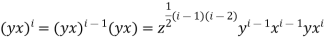
Since, by then follows at once, that is,
Hence 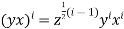 for all i
for all i
Q9) Explain the Multiplicative group of integers modulo n?
A9)
The multiplicative group of integers modulo n is formed by multiplying the integers coprime (roughly prime) to n from the set of n non-negative integers in modular arithmetic. The constituents of this group are equivalently thought of as coprimeto n congruence classes, commonly known as residues modulo n. As a result, the group of primitive residue classes modulo is another name for it.
It is defined as the group of units of the ring of integers modulo n in ring theory, a part of abstract algebra. In this ring, units refers to elements with a multiplicative inverse, which are all coprimeto n.
In number theory, this group, which is commonly designated, is crucial. It's used in cryptography, integer factorization, and primality testing, among other things
Q10) “Let H1, . . . ,Hn ≤ G. Then, φ : H1 ×···×Hn→ G defined by φ(h1, . . . , hn) = h1 hn is an isomorphism if and only if the Hi’s satisfy the IDP properties.” Prove this.
A10)
Assume that φ [as in the statement] is an isomorphism. Let G˜ def = H1 × ···×Hn and H˜idef = {1} ×··· {1} × Hi × {1} ×···× {1} ≤ G˜ [with Hi in the i-th coordinate]. Then, clearly φ(H˜i) = Hi . Since H˜i C G˜ , we have that Hi C G, as φ is an isomorphism [by assumption].
Thus, IDP property (1) is proved. Since φ is an isomorphism [and hence onto] and φ(G˜) = H1 ···Hn [by definition of φ and the product of groups], we have that G = H1 ···Hn, proving property (2).
Now, let H ˆ˜ idef = H1 × ···× Hi−1 × {1} × Hi+1 ×···×Hn. Then, clearly φ(H ˆ˜i) = Hˆi [with Hˆi as in Definition 2] and H˜i∩ H ˆ˜i = {(1, . . . , 1)}. Thus
{1} = φ({(1, . . . , 1)})
= φ(H˜i∩ H ˆ˜i) [as noted above]
= φ(H˜i) ∩φ(H ˆ˜i) [as φ is a bijection– this is a Math 300 exercise]
= Hi ∩ Hˆi [as noted above]
Hence, property (3) is also satisfied.
Q11) Let G be a non-abelian simple group. Let D(G)=[G,G] be the commutator subgroup of G. Show that G=D(G).
A11)
Note that the commutator subgroup D(G) is a normal subgroup.
Since G is simple, any normal subgroup of G is either the trivial group {e} or G itself. Thus we have either D(G)={e} or D(G)=G.
If D(G)={e}, then for any two elements a,b∈G the commutator [a,b]∈D(G)={e}.
Thus we have
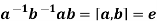
Therefore we have ab=ba for any a,b∈G. This means that the group G is abelian, which contradicts with the assumption that G is non-abelian.
Therefore, we must have D(G)=G as required.
Q12) Let K,N be normal subgroups of a group G. Suppose that the quotient groups G/K and G/N are both abelian groups.
Then show that the group 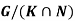
A12)
By the lemma mentioned above, we know that G/K is an abelian group if and only if the commutator subgroup D(G)=[G,G] is contained in K.
Similarly, since G/N is abelian, D(G) is contained in N.
Therefore, the commutator subgroup D(G)⊂K∩N. This implies, again by Lemma, that the quotient group
G/(K∩N)
Q13) Let G be an abelian group and let f: G→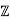 be a surjective group homomorphism.
be a surjective group homomorphism.
Prove that we have an isomorphism of groups:
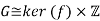
A13)
Since f: G→Z is surjective, there exists an element a∈G such that

Let H=⟨a⟩be the subgroup of G generated by the element a.
We show that G≅ker(f)×H
To prove this isomorphism, it suffices to prove the following three conditions.
- The subgroups ker(f) and H are normal in G.
- The intersection is trivial: ker(f)∩H={e}, where e is the identity element of G.
- Every element of G is a product of elements of ker(f) and H. That is, G=ker(f)H.
The first condition follows immediately since the group G is abelian, hence all the subgroups of G are normal.
To check condition 2, let x∈ker(f)∩H.
Then x=an for some n∈Z and we have
 since
since 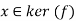

 since f is a homomorphism
since f is a homomorphism
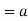 since f(a)=1
since f(a)=1
Thus, as a result we have x=a0=e, and hence ker(f)∩H={e}.
As a result, condition 2 is satisfied.
Let b be any arbitrary element in G to prove condition 3.
Let n=f(b)∈ . Then we have
. Then we have
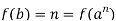
And thus we have
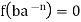
It follows that ba−n∈ker(f).
So there exists z∈ker(f) such that ba−n=z.
Therefore we have
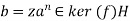
This implies that G=ker(f)H.
As a result of proving all of the prerequisites, we are able to obtain.
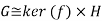
H is isomorphic to Z because it is an infinite-order cyclic group.
(There exists a positive integer n such that an=e if H has a finite order.) Then there's
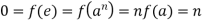
And this is in opposition to n's positivity.)
When these isomorphisms are combined, we get

As required.
Q14) A group that is not a non-trivial direct product
A14)
The symmetric group S3 has six elements:
S3 = {e,(1 2),(1 3),(2 3),(1 2 3),(1 3 2)}.
This group is not abelian: consider, for example, the products (1 2)(1 3) and (1 3)(1 2).
If S3 could be written as a non-trivial direct product – that is, as a direct product in which neither subgroup has order 1 – it would have to be as the direct product of subgroups of orders 2 and 3.
The group S3 does possess subgroups of orders 2 and 3. For example, H1 = {e,(1 2)} has order 2 and H2 = {e,(1 2 3),(1 3 2)} has order 3.
However, any subgroup of order 2 is cyclic and is isomorphic to 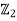 . Equally, any subgroup of order 3 is cyclic and is isomorphic to
. Equally, any subgroup of order 3 is cyclic and is isomorphic to 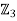 . It follows, therefore, that any attempt to form a direct product of such subgroups leads to a group isomorphic to
. It follows, therefore, that any attempt to form a direct product of such subgroups leads to a group isomorphic to 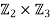 , which is abelian by Exercise 1.4 and so not isomorphic to S3.
, which is abelian by Exercise 1.4 and so not isomorphic to S3.
Q14) Show that if a group G has the following order, then it is not simple.
- 28
- 496
- 8128
A15)
(1) A group of order 28
Note that 28=22⋅7. The number n7 of the Sylow 7-subgroups of G satisfies
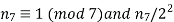
Thus, the only possible value is n7=1. The unique Sylow 7-subgroup is a proper nontrivial normal subgroup of G, hence G is not simple.
(2) A group of order 496
Note that 496=24⋅31. By the same argument as in (1), there is a normal Sylow 31-subgroup in G, hence G is not simple.
(3) A group of order 8128
We have 8128=26⋅127, where 127 is a prime number.
Again the same reasoning proves that the group G has the unique normal Sylow 127-subgroup in G, hence G is not simple.
Q15) If the order is an even perfect number, a group is not simple
A16)
From elementary number theory, all even perfect numbers are of the form
 ,
,
Where pp is a prime number and 2p−1 is also a prime number.
(For a proof, see the post “Even Perfect Numbers and Mersenne Prime Numbers“.)
Suppose the order of a group GG is 2p−1(2p−1), with prime p, 2p−1.
Then the number n2p−1 of Sylow (2p−1)-subgroup satisfies
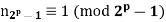 and
and 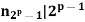
These force that n2p−1=1.
Therefore the group G contains the unique normal Sylow (2p−1)-subgroup, hence G is not simple.
Q16) Determine whether a group GG of the following order is simple or not.
(a) |G|=100.
(b) |G|=200.
A17)
(a) When |G|=100.
The prime factorization of 100 is 22⋅52. Let us determine the number n5 of 5-Sylow subgroup of G.
By Sylow’s theorem, we know that n5≡1(mod5) and n5 divides 22.
The only number satisfies both constraints is n5=1. Thus there is only one 5-Sylow subgroup of G. This implies that the 5-Sylow subgroup is a normal subgroup of G.
Since the order of the 5-Sylow subgroup is 25, it is a proper normal subgroup. Thus, the group G is not simple.
(b) When |G|=200
The prime factorization is 200=23⋅52.
We again consider the number n5 of 5-Sylow subgroups of G.
Sylow’s theorem implies that n5≡1(mod5) and n5 divides 23.
These two constraints has only one solution n5=1.
Thus the group G has a unique proper normal 5-Sylow subgroup of order 25.
Hence G is a simple group.
Q17) Prove that the union H1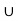 H2 is never a subgroup in G.
H2 is never a subgroup in G.
A18)
Seeking a contradiction, let us assume that the union H1∪H2 is a subgroup of G.
Since H1⊄H2, there exists an element a∈H1 such that a∉H2.
Similarly, as H2⊄H1, there exists an element b∈H2 such that b∉H1.
As we are assuming H1∪H2 is a group, we have ab∈H1∪H2.
It follows that either ab∈H1 or ab∈H2.
If ab∈H1, then we have
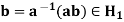
Which contradicts the choice of a.
In either case, we reached a contradiction.
Thus, we conclude that the union H1∪H2 is not a subgroup of G.
Q18) Prove that a group cannot be written as the union of two proper subgroups.
A19)
If a group G is a union of two proper subgroup H1 and H2, then we must have H1⊄H2 and H2⊄H1, otherwise G=H1 or G=H2 and this is impossible as H1,H2 are proper subgroups.
Then G=H1∪H2 is a subgroup of G,
Thus, any group cannot be a union of proper subgroups.
Q19) Prove that every cyclic group is abelian.
A20)
Let G be a cyclic group with a generator g∈G.
Namely, we have G=⟨g⟩ (every element in G is some power of g.)
Let a and b be arbitrary elements in G.
Then there exists n,m∈Z such that a=gn and b=gm.
It follows that
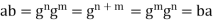
Hence we obtain ab=ba for arbitrary a,b∈G.
Thus G is an abelian group.