Unit - 4

Groups acting on themselves by conjugation

Q1) What is Cauchy's integral theorem? And prove the theorem?

A1)

The Cauchy integral theorem (sometimes known as the Cauchy–Goursat theorem) is a key statement regarding line integrals for holomorphic functions in the complex plane, named after Augustin-Louis Cauchy (and ÉdouardGoursat). It states that if two separate pathways connect the same two points and a function is holomorphic everywhere in between the two paths, then the function's two path integrals will be the same.

Proof

If one assumes that the partial derivatives of a holomorphic function are continuous, the Cauchy integral theorem can be proved as a direct consequence of Green's theorem and the fact that the real and imaginary parts of 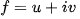 must satisfy the Cauchy–Riemann equations in the region bounded by , and moreover in the open neighborhood U of this region. Cauchy provided this proof, but it was later proved by Goursat without requiring techniques from vector calculus, or the continuity of partial derivatives.

The integrand f, as well as the differential dz, can be broken down into real and imaginary components:

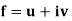
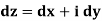
In this case we have

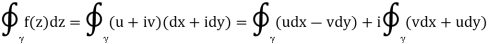
By Green's theorem, we may then replace the integrals around the closed contour {\displaystyle \gamma } with an area integral throughout the domain {\displaystyle D}D that is enclosed by{\displaystyle \gamma }  as follow

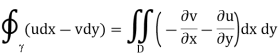
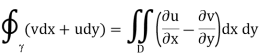
However, because u and v are the real and imaginary components of a holomorphic function in the domain D, they must fulfil the Cauchy–Riemann equations there:

{\displaystyle {\frac {\partial u}{\partial x}}={\frac {\partial v}{\partial y}}}

{\displaystyle {\frac {\partial u}{\partial x}}={\frac {\partial v}{\partial y}}}

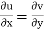
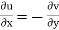
As a result, both integrands (and hence their integrals) are zero.

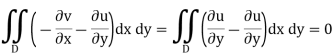
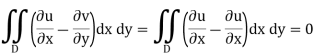
This gives the desired result

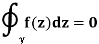
Q2) Prove:

If G is a group such that o (G) =pq where p<q p,q are primes and p ∤ q-1. Then G is cyclic?

A2)

By Sylow’s First Theorem G has atleast on Sylow p-subgroup and one Sylow q-subgroup. By Sylow’s Second Theorem, the number of Sylow p-subgroup is 1+kp where 1+kp∣q Thus 1+kp = 1 or q

If 1+kp = 1 then sylow p-subgroup is unique hence normal in G hence G has a proper Normal subgroup thus G is not simple then we are through Again by Sylow’s Second Theorem, the number of Sylow q-subgroup is 1+kq where 1+k’q∣p Thus 1+k’q = 1 or p If 1+k’q = 1 then sylow q-subgroup is unique hence normal in G hence G has a proper Normal subgroup thus G is not simple again we are through If 1+k’q = p then k’q = p – 1 which means that q ∣p – 1 which is not true. Now o (H) = p, o (K) = q, and H ∩ K is a subgroup of both H and K. ∴o(H ∩ K) | p and o(H ∩ K) | q ⇒ o(H ∩ K) | (p,q ) ⇒o(H ∩ K) | 1 ⇒o(H ∩ K) | = 1 ⇒H ∩ K = {e}

We know if H and K are normal subgroups of G such that H ∩ K = {e}, Then hk = kh∀ h ∈ H and k ∈ K. Now H and K, being groups of prime orders, are cyclic. ∴ let H = , K = so that o (a) = o (H) =p, o (b) = o (K) = q Now ab=ba [because hk = kh∀ h ∈ H and k ∈ K]. And (o (a), o (b)) = (p, q) =1 Therefore o (ab) = o (a). o (b) = pq=o (G) Thus G has an element ab of order pq thus G is cyclic. After proving the result 2.7 the group satisfying the condition of 2.7 will always be cyclic group and as cyclic group is always abelian and by using 2.1 abelian group of composite order is not simple.

Q3) Explain the Sylow's test?

A3)

Let n be a non-prime positive integer, and p be a prime divisor of n. There is no simple group of order n if 1 is the only divisor of n that is congruent to 1 modulo p.

Proof:

If n is a prime-power, then a group of order n has a nontrivial center and, therefore, is not simple. If n is not a prime power, then every Sylow subgroup is proper, and, by 

According to Sylow's Third Theorem, the number of Sylow p-subgroups of an order n group is equal to 1 modulo p and divides n. The Sylow p-subgroup is unique since 1 is the only such number, and hence it is normal. The group is not simple since it is a proper, non-identity subset.

Q4) Explain the Consequences of Sylow's theorem?

A4)

According to the Sylow theorems, for any prime number p, every Sylow p-subgroup has the same order, p. In contrast, if a subgroup has order p, it is a Sylow p-subgroup and is hence isomorphic to all other Sylow p subgroups. If h is any p-subgroup of G, then H is a subgroup of a p subgroup of order p due to the maximality criterion.

A very important consequence of Theorem 2 is that the condition 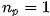 is equivalent to saying that the Sylow p-subgroup of G is a normal subgroup. However, there are groups that have normal subgroups but no normal Sylow subgroups, such as .

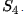Q5) Prove the  Sylow's theorem?

A5)

The Sylow theorems are a set of theorems in mathematics, specifically in the subject of finite group theory, named after the Norwegian mathematician Peter Ludwig Sylow. They provide extensive information regarding the number of fixed order subgroups that a given finite group possesses. The Sylow theorems are significant in the categorization of finite simple groups and are a key aspect of finite group theory.

For a prime number P, a Sylow p-subgroup (sometimes p-Sylow subgroup) of a group G is a maximal P-subgroup of G, i.e., a subgroup of G that is a p-group (so that the order of every group element is a power of P) that is not a proper subgroup of any other P-subgroup of G. The set of all Sylow P-subgroups for a given prime P is sometimes written 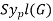{\displaystyle {\text{Syl}}_{p}(G)}

The Sylow theorems state that Lagrange's theorem has a partial converse. The order (number of elements) of every subgroup of every finite group G divides the order of G, according to Lagrange's theorem. According to the Sylow theorems, there exists a Sylow P-subgroup of G of order P, the maximum power of P that divides the order of for any prime factor P of the order of a finite group G. Furthermore, every Sylow P-subgroup of P is a subgroup of order G, and the Sylow G-subgroups of a group (for a given prime P) are conjugate. Furthermore, for a given prime P, the number of Sylow P-subgroups of a group is equivalent to

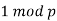
Q6) Prove: Suppose σ ∈ Sn, and let m1, m2, …mr be the distinct integers (including 1 if applicable) in the cycle type of σ, and let there be ki cycles of order mi in σ. (Thus ∑kimi=n). Then the number of conjugates of σ is exactly

n!(k1!mk11)(k2!mk22)⋯(kr!mkrr) 

A6)

The number of cycles of a certain cycle type determines the size of a conjugacy class. Select a cycle type and arrange the cycles in a logical order. Consider the n!n! different ways to fill the ”‘holes”' in the cycles with integers ranging from 1 to n. If two similar arrangements describe the same permutation, they are said to be comparable. The fact that this is an equivalence relation and that it splits the configurations is obvious. The size of each equivalence class will be determined.

Consider a specific configuration (a permutation), and the ki cycles of order mimi in that configuration. Each cycle can be written in a variety of ways (by starting with a different element). The cycles can also appear in any of ki! possible orders while still indicating the same permutation. Thus if, for example, ki=2 and the first cycle contains a1,…al while the second contains b1,…,b1, that is the same permutation as if the first cycle contained b1,…,bl and the second contained a1,…,all. So there are ki!mkiiki!⁢miki equivalent permutations considering the cycles of order mi. So the total number of permutations, considering each of the possible cycle orders, equivalent to the given permutation is

(k1!mk11)(k2!mk22)…(kr!mkrr)

Q7) Prove this: Two permutations σ, τ∈Sn are conjugate if and only if they have the same cycle type.

A7)

Assume first that σσ and ττ are conjugate; say τ=σ1σσ−11. Write σ as a product of disjoint cycles

(α1…αa)(β1…βb)(…)(α1⁢…⁢α)…)

To show that σσ and ττ have the same cycle type, it clearly suffices to show that if jj follows ii in the cycle decomposition of σσ, then σ1(j)σ1⁢(j) follows σ1(i)σ1⁢(i) in the cycle decomposition of ττ. But suppose σ(i)=jσ⁢(i)=j. Then

τ(σ1(i))=σ1σσ−11(σ1(i))=σ1σ(i)=σ1(j) 

And we are done.

Assume that and share the same cycle type. Write each permutation's cycle decomposition in such a way that the cycles are listed in non descending order of length (including cycles of length 1). Then there's (for example)

(a1)(a2a3a4)(a5…an)=(a1)

=(b1)(b2b3b4)(b5…bn)=(b1)*(b2*b3*b4)*(b5*…*bn)

=(a1)(a2a3a4)(a5…an)=(a1)⁢(a2⁢a3⁢a4)⁢(a5⁢…⁢an) 

Define σ1σ1 to be the permutation that takes aiai to bi. Clearly σ∈Sn, since each of 1,…,n1,…,n appears exactly once among the aiai and once among the bi. But also, since the cycle types of σσ and ττ match, we see that

σ1σ−1(bi)=σ1σ(ai) where aj, bj are the ‘next’ elements in their respective cycles. Thus τ=σ1σ−1 and we are done.

Q8) Prove: Up to the ordering of the cycles and a cyclic permutation of the elements within each cycle, every permutation in Sn has a cycle decomposition that is unique.

A8)

We construct the cycle decomposition for σ∈Sn. Let X={1,…,n}, and regard σ as acting on X. Let G=⟨σ⟩ be the subgroup of Sn generated by σ. Then G acts on X, so by the orbit-stabilizer theorem, it partitions XX into a unique set of orbits. In addition, for any orbit Gx, we have that

σix↔σiGxx

Is a bijection, where Gx is the stabilizer of x in G.

Now, G=⟨σ⟩ is cyclic and thus G/Gxis cyclic as well; its order is the smallest power dd of σ such that σd∈Gx Note also that d=|Gx|=[G:Gx] Using the explicit bijection above, we see that the unique cosets of Gx in G are

Gx,σGx,…,σd−1GxGx,

And that the elements of Gx are

x,σx,…,σd−1xx,

Thus on any orbit of size d, σ is a d-cycle. This shows that a cycle decomposition exists.

Because the cycle specified by on an element of order d is uniquely determined by construction from the element, uniqueness follows simply. Instead, choosing a different element in the same orbit, such as jx, yields

σjx,σj+1x,…,σd−1x,x,σx,…,σj−1x

Which is the same cycle permuted left by j.

Q9) Explain the Conjugacy as group action?

A9)

If we define

g . x = gxg−1

We have a group action of G on G for any two elements g and x in G. The conjugacy classes are the orbits of this action, and the centralizer of a particular element is the stabiliser.

Similarly, we can write "G group action on all subsets of G" to define a group action of G on the set of all subsets of G.

g . S = gSg−1,

Or on the set of the subgroups of G.

Q10) What is conjugation?

A10)

Two elements a and b of a group are conjugate in mathematics, especially group theory, if the group has an element g such that b = g-11ag. This is an equivalence relation with conjugacy classes as equivalence classes.

Because members of the same conjugacy class can't be identified only by their group structure, they share a lot of characteristics. The study of non-abelian groups' conjugacy classes is essential for understanding their structure. Each conjugacy class for an abelian group is a set of one element (singleton set).

Class functions are functions that are constant for members of the same conjugacy class.

Let G stand for a group. If there is an element g in G such that gag1 = b, two elements a and b of G are conjugate. Also, b is a conjugate of a, and an is a conjugate of b, according to some.

The conjugacy relation is known as matrix similarity in the case of the group GL(n) of invertible matrices.

Conjugacy can be simply demonstrated to be an equivalence relation, which divides G into equivalence classes. (This indicates that each group member belongs to only one conjugacy class, with Cl(a) and Cl(b) being same if and only if a and b are conjugate, and disjoint otherwise.) In G, the equivalence class containing the element an is

Cl(a) = { gag−1 | g ∈ G }

Q11) Let G be a group of order |G|=pn for some n∈N.

(Such a group is called a p-group.)

Show that the center Z(G) of the group G is not trivial.

A11)

If G=Z(G), then the statement is true. So suppose that G≠Z(G).

Then by the class equation, we have

Where gi are representatives of the distinct conjugacy class not contained in the center Z(G), and CG(gi) is the centralizer of gi.

(Since we are assuming that G≠Z(G) such gi exist.)

Since gi∉Z(G), the groups CG(gi) are proper subgroups of G and

Hence p divides |G:CG(gi)|. Of course pp divides |G|, thus p should

Divide |Z(G)| as well.

Therefore the center Z(G) cannot be trivial.

Q12) Let G be a group of order 57. Assume that G is not a cyclic group.

Then determine the number of elements in G of order 3.

A12)

Observe the prime factorization 57=3⋅19.

Let n19 be the number of Sylow 19-subgroups of G.

By Sylow’s theorem, we know that

n19≡1(mod19) and n19∣3

It follows that n19=1.

Now, observe that if g∈G, then the order of g is 1, 3, or 19. Note that since G is not a cyclic group, the order of g cannot be 57.

As there is exactly one Sylow 19-subgroup P, any element that is not in P must have order 3.

Therefore, the number of elements of order 3 is 57−19=38

Q13) Let G be a group of order 12. Prove that G has a normal subgroup of order 3 or 4.

A13)

Since 12=22⋅3, a Sylow 2-subgroup of G has order 4 and a Sylow 3-subgroup of G has order 3.
Let np be the number of Sylow p-subgroups in G, where p=2,3.

Recall that if np=1, then the unique Sylow p-subgroup is normal in G.

By Sylow’s theorem, we know that n2∣3, hence np=1,3.

Also by Sylow’s theorem, n3≡1(mod3) and n3∣4.

It follows that n3=1,4.

If n3=1, then the unique Sylow 3-subgroup is a normal subgroup of order 3.

Suppose that n3=4. Then there are four Sylow 3-subgroup in G.

The order of each Sylow 3-subgroup is 3, and the intersection of two distinct Sylow 3-subgroups intersect trivially (the intersection consists of the identity element) since every non-identity element has order 3.

Hence two elements of order 3 in each Sylow 3-subgroup are not included in other Sylow 3-subgroup.

Thus, there are totally 4⋅2=8 elements of order 3 in G.

Since |G|=12, there are 12−8=4 elements of order not equal to 3.

Since any Sylow 2-subgroup contains four elements, these elements fill up the remaining elements.

So there is just one Sylow 2-subgroup, and hence it is a normal subgroup of order 4.

In either case, the group G has a normal subgroup of order 3 or 4.

Q14) Evaluate 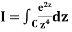 where C:|z|=1.

A14)

With Cauchy’s formula for derivatives this is easy. Let f(z)=e2z. Then,

Let C represent the contour given below, and assess the same integral as before.

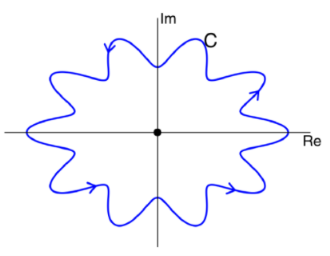
The integral is the same as the previous example, i.e.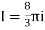

Q15) Compute  dz over the contour shown.

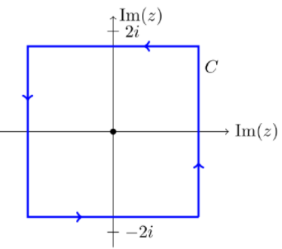
A15)

Let f(z)=cos(z)/(z2+8). f(z) is analytic on and inside the curve C. That is, the roots of z2+8 are outside the curve. So, we rewrite the integral as

Q16) Compute 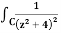dz over the contour shown.

A16)

The denominator is factored as

Let

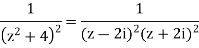
Let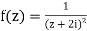

Inside C, clear f(z) is analytic. So, according to Cauchy's derivatives formula:

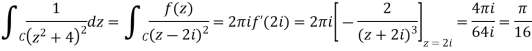
Q17) Let G be a group of order 520=23⋅5⋅13. Letting np denote the number of Sylow p-subgroups of G, we see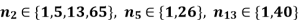

A17)

Suppose neither n2,n5 nor n13 equals 1 (else we're done). Then n13=40 and there are 40(13−1)=480 elements of order 13. Similarly, n5=26 and there are 26(5−1)=104 elements of order 5. This means G contains at least 480+104=584 elements, which is impossible. Hence at least one of n2,n5 or n13 equals 1 and so G is not simple.

Q18) Let G be a finite group of order 231=3.7.11.

Prove that every Sylow 11-subgroup of G is contained in the center Z(G).

A18)

We first claim that there is a unique Sylow 11-subgroup of G.
Let n11 be the number of Sylow 11-subgroups in G.

By Sylow’s theorem, we know that

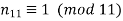
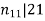
By the first condition, n11=1,12,23⋯ and only n11=1divides 21.

Thus, we have n11=1 and there is only one Sylow 11-subgroup P11 in G, and hence it is normal in G.

Now we consider the action of G on the normal subgroup P11 given by conjugation.
The action induces the permutation representation homomorphism

Where Aut(P11) is the automorphism group of P11.

Note that P11 is a group of order 11, hence it is isomorphic to the cyclic group 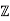/11.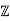
Recall that

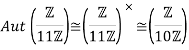
The first isomorphism theorem gives

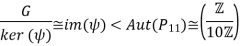
Hence the order of G/ker(ψ) must be a divisor of 10.

Since |G|=231=3⋅7⋅11, the only possible way for this is |G/ker(ψ)|=1| and

Thus ker(ψ)=G.

This implies that for any g∈G, the automorphism ψ(g):P11→P11 given by h↦ghg−1 is the identity map.

Thus, we have ghg−1=hg for all g∈G and h∈H.

It yields that P11 is in the center Z(G) of G.

Q19) Prove that G is a cyclic group.

A19)

Note the prime factorization 217=7⋅31.

We first determine the number npnp of Sylow p-group for p=7,31.

Recall from Sylow’s theorem that

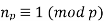
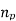divides n/p

Thus, n7 could be 1,8,15,22,29,… and n7 needs to divide 217/7=31.

Hence the only possible value for n7 is n7=1.

So there is a unique Sylow 7-subgroup P7 of G.

By Sylow’s theorem, the unique Sylow 7-subgroup must be a normal subgroup of G.

Similarly, n31=1,32,… and n31 must divide 217/31=7, and hence we must

Have n31=1.
Thus G has a unique normal Sylow 31-subgroup P31.

Note that these Sylow subgroup have prime order, and hence they are isomorphic to cyclic groups:

and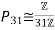

It is also straightforward to see that P7∩P31={e}P7∩P31={e}, where ee is the identity element in GG.

In summary, we have

1. P7,P31 are normal subgroups of G.
2. P7∩P31={e}.
3. |P7P31|=|G|.

These yields that GG is a direct product of P7 and P31, and we obtain

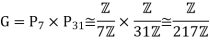
Hence G is a cyclic group.

Q20) Determine the number of generators of the group G.

A20)

Recall that the number of generators of a cyclic group of order n is equal to the number of integers between 1 and n that are relatively prime to n.
Namely, the number of generators is equal to ϕ(n), where ϕ is the Euler totient function.

We know that G is a cyclic group of order 217.

Thus, the number of generators of G is

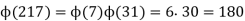
Where the first equality follows since ϕ is multiplicative.