Unit - 4

Affine ciphers

Q1) What is Hill Ciphers.

A1)

Hill cyphers (developed in 1929) are a type of block cypher in which the ciphertext character that replaces a certain plaintext character in the encryption is determined by the plaintext characters surrounding it. Matrix arithmetic is used to encrypt the information.

A square matrix of integers is used as the encryption key for a Hill cypher. These integers are drawn from the range 0 to 1, inclusive, n 1, where n is the size of the plaintext message character set. (If you use the standard English alphabet, n = 26.) It's worth noting that not all such square matrices are valid Hill cypher keys. Later, we'll go over what's required to create a valid key.

For now, suppose the key is the matrix 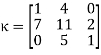and we want to encrypt the message “time to study” using a Hill cipher with this key. Using the conversion table:

0 1 2 3 4 5 6 7 8 9 10 11 12

A B C D E F G H I J K L M             

13 14 15 16 17 18 19 20 21 22 23 24 25

N O P Q R S T U V W X Y Z

Our plaintext message is represented as. 19:8:12:4:19:14:18:19:20:3:24:19:8:12:4 We now divide this sequence of numbers into three rows of length three (the size of ) to get

19 8 12

4 19 14

18 19 20

3 24  ?

In order for the encryption to continue, we must address the “?” in the last row. It's common practise to replace it with an integer that represents a plaintext letter that can be easily identified as unwanted when the message is received. We'll utilise the number 23, which stands for the letter "x." From the four rows that result, we create a matrix:

We now compute = using standard matrix multiplication, except that anytime an element x does not meet 0 x 25, we replace x with the integer y 0..., 25 so that y x (mod 26). As an example, in the current situation, this produces in

To get the ciphertext XQCHJAVRGPBT, concatenate the rows of to get the sequence 23 16 2 7 9 0 21 17 6 15 1 19 and replace each number with the letter it represents.

Try encrypting the plaintext "finals are coming" with the encryption key above using a Hill cypher, and see if you can produce the ciphertext JRDZDOPZMWOOVXG.

Using a Hill cypher and the same encryption key as before, the following ciphertext was generated:

COAOVZOZWJBH.

To produce the sequence 2 14 0 14 21 25 14 25 22 9 1 7, replace each ciphertext letter with the integer that represents it.

We now need to acquire from and. We could solve: if the connection (mod 26) were an equation instead of a congruence and an invertible matrix.

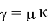
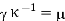
Since we have a congruence and not an equation, we have to take more care than this! There are two issues: do we have an inverse for κ, and, if so, what do we do if, (as is likely), κ −1 has non-integer entries? In this case, (as you can verify), we do have an inverse for κ:

This inverse, on the other hand, does not have integer elements. To continue with our decryption, we must substitute 1 27 with an integer that behaves similarly, i.e., when multiplied by 27, provides an answer that is equivalent to 1 modulo 26. (For further information, see the section on affine cyphers.) Fortunately, since 27 1 (mod 26), we can substitute 1 27 for 1 to get:

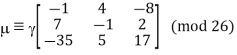
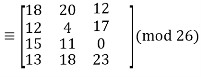
The plaintext “summerplansx” is recovered from here, and we determine that the message was “summer plans.” We can now determine what properties a square matrix of integers must have in order to be a valid key for a Hill cypher. We need to be invertible modulo 26 for the decryption process to work, which means that the determinant of must satisfy gcd(det, 26) = 1. (To understand the relationship between determinants and inverses, look up the classical adjoint of a matrix in your favourite linear algebra source.) Here's some additional practise for you. The ciphertext below was created by

a Hill cipher with key

EMRISXCAEGOHJEVI. Check to see if the plaintext can be recovered. (Keep in mind that your matrices and must have two columns if you're using a 2 2 key!) While Hill cyphers provide a major boost in security over Vigenere cyphers, they are vulnerable to known plaintext attacks if a few right characters of plaintext are previously matched to a ciphertext message. As a result, Hill cyphers aren't seen to be safe enough for sensitive applications.

Q2) What is Affine ciphers.

A2)

The affine cypher is a monoalphabetic substitution cypher in which each letter of the alphabet is mapped to its numeric counterpart, encrypted with a simple mathematical function, and then transformed back to a letter. Because of the formula, each letter encrypts to one other letter and back, the cypher is effectively a substitution cypher with a rule determining which letter goes to which. As a result, it suffers from the same flaws as all other substitution cyphers. The function (axe + b) mod 26 is used to encode each letter, with b indicating the magnitude of the shift.

The letters of an alphabet of size m are first mapped to integers in the range 0... m 1 in the affine cypher. The integer that each plaintext letter refers to is then transformed into another integer that corresponds to a ciphertext letter using modular arithmetic. For a single letter, the encryption function is

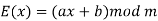
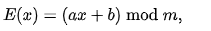
The size of the alphabet is modulus m, and the cipher's keys are a and b. a must be chosen in such a way that a and m are coprime. The function of decryption is

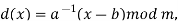
Where a−1 is the modular multiplicative inverse of a modulo m. I.e., it satisfies the equation

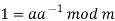
If a and m are coprime, the multiplicative inverse of a exists. Decryption may not be possible without the restriction on a. The decryption function is the inverse of the encryption function, as shown below.

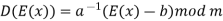
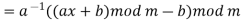
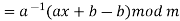
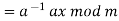
Q3) State RSA encryption and description.

A3)

• The RSA algorithm is a public key encryption technology that is widely regarded as the most secure. Rivest, Shamir, and Adleman devised the RSA algorithm in 1978, hence the name.

• In the standard alphabet, there are 12 numbers smaller than 26 that are coprime to 26, and each of them has 26 potential values for b, giving us a total of 12 x 26 = 312 keys for the Affine Cipher.

Algorithm

• The RSA algorithm is a common exponentiation in a finite field over integers, including prime numbers, with sufficiently large integers to make it difficult to solve.

• This algorithm uses two sets of keys: a private key and a public key. To work on the RSA algorithm, you must go through the stages below.

• Generate the RSA modulus in step one.

The first step is to choose two prime numbers, p and q, and then calculate their product N, as illustrated in the diagram.

N=p*q

Let N be the specified huge number in this case.

• Derived Number (Step 2)

Consider e as a derived number that must be larger than 1 but less than (p-1) and (q-1) The fundamental criterion will be that no common factor of (p-1) and (q-1) other than 1 exists.

• Step 3: Generate a public key

The RSA public key is formed by the stated pair of numbers n and e, and it is made public.

• Step 4: Obtaining a Private Key

The numbers p, q, and e are used to calculate Private Key d. The following is the mathematical relationship between the numbers:

1 mod (p-1) = ed (q-1)

The basic formula for the Extended Euclidean Algorithm, which takes p and q as input parameters, is shown above.

Encryption Formula

Consider the case of a sender who sends a plain text message to a recipient whose public key is (n,e). Use the following to encrypt the plain text message in the given case.

Syntax −

C = Pe mod n

Decryption Formula

The decryption process is simple and contains analytics for computation in a methodical manner. The result modulus will be calculated as if receiver C possesses the private key d.

Q4) What is public Key Cryptography?

A4)

It's time to find out our public key now that we know Carmichael's totient of our prime numbers. Public keys in RSA are made up of a prime integer e and modulus n. (we will explain what modulus means in a few paragraphs). The value for (n) in our case is 349,716. The number e can be any number between 1 and the value for (n).

It's less crucial for e to be a random value because the public key is released publicly. In reality, e is usually set to 65,537 because choosing significantly larger integers at random reduces the efficiency of encryption. To make calculations easier, we'll keep the numbers small in today's example. Assume the following scenario:

e = 11

The ciphertext is the name given to our finished encrypted data (c). We get it from our plaintext message (m) by using the following formula using the public key:

c = me mod n

The public key is e mod n, as previously stated. We've previously figured out e, and we're familiar with n. Mod is the only thing we need to explain. It's a touch beyond the scope of this article, but a modulo operation refers to the residual left over when you divide one side by the other. Consider the following scenario:

10 mod 3 = 1

This is due to the fact that 3 is multiplied by 10 three times, leaving a leftover of 1.

Let's get back to our problem. Let's pretend that the message (m) we wish to encrypt and keep secret is only a single number, 4, to keep things easy. Let's get everything set up:

c = me mod n

c = 411 mod 701,111

c = 4,194,304 mod 701,111

We'll use an internet calculator to simplify the modulo process, but you're welcome to figure it out on your own. We get the following results by typing 4,194,304 into the online calculator:

c = 688,749

As a result, when we encrypt our message with RSA and our public key, we get a ciphertext of 688,749. The preceding steps may have appeared a little too math-heavy at first, but it's vital to remember what happened.

We had a four-message message that we intended to keep hidden. We used a public key to encrypt the result, which came out to 688,749. We can securely deliver the number 688,749 to the owner of the key pair now that it has been encrypted. With their private key, they will be the only ones who can decode it. They'll be able to view the message we were actually transmitting once they decrypt it.

Q5) What is Fermat’s Last Theorem.

A5)

Fermat's Last Theorem's proof symbolises the end of an era in mathematics. Given that practically all of the techniques that were subsequently used to solve the problem had not yet been devised at the time of Fermat, it's intriguing to hypothesise whether he had an elementary proof of the theorem. Fermat's stated proof appears to have been illusionary, based on the tenacity with which the problem eluded attack for so long. This conclusion is further supported by the fact that Fermat searched for proofs for the cases n=4 and n=5, which would have been superfluous had he actually been in possession of a general proof.

In the  episode of the television program The Simpsons, the equation  appeared at one point in the background. Expansion reveals that only the first 9 decimal digits match (Rogers 2005). The episode The Wizard of Evergreen Terrace mentions , which is correct not just in the first ten decimal places, but also in the last decimal place, which is easy to examine (Greenwald). Captain Picard says that learning Fermat's Last Theorem is a calming procedure in the Star Trek: The Next Generation episode "The Royale."

Q6) Assume the message is encrypted by the function y = (11x + 4) MOD 26 (Encipher)

A6)

To encrypt the plaintext MONEY, we first convert each letter in plaintext into a numerical value between 0 and 25 according to following list

A – 0

B – 1

C – 2

D – 3

.

.

.

Z – 25

Thus, the numerical values corresponding to the plaintext MONEY are 12, 14, 13, 4, and 24.
Applying the given function for each numerical value, we have

M: y = (11*12 + 4) MOD 26 = 6
O: y = (11*14 + 4) MOD 26 = 2
N: y = (11*13 + 4) MOD 26 = 17
E : y = (11*4 + 4) MOD 26 = 22
Y : y = (11*24 + 4) MOD 26 = 8

The corresponding letters are GCRWI, which is the ciphertext.

(Decipher)

To decipher, we transform the function y as:
x = inverse (a) (y – b) MOD m
Then we have, x = inverse(11) (y – 4) MOD 26
Inverse(11) MOD 26 = 19, and the decryption function will be x = 19 (y – 4) MOD 26

We now decipher the ciphertext GCRWI by applying the decryption function. We have:

G: x = 19*(6-4) MOD 26 = 12
C: x = 19*(2-4) MOD 26 = 14
R: x = 19*(17-4) MOD 26 = 13
W: x = 19*(22-4) MOD 26 = 4
I: x = 19*(8-4) MOD 26 = 24

The corresponding plaintext letters are MONEY.

Q6) Encipher ITS COOL with

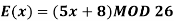
A7)

Filling in the following table gives

	8	19	18	2	14	14	11
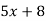	48	103	98	18	78	78	63
	22	25	20	18	0	0	11
Cipher	W	Z	U	S	A	A	L

If y = E(x) = (ax+b) MOD 26, then we can “solve for x in terms of y” and so determine E−1 (y). That is, if y ≡ (ax + b) (mod 26), then y − b ≡ ax (mod 26), or equivalently ax ≡ (y − b) (mod 26). Using our earlier results, we see that if we multiply both sides by a −1 (mod 26), then x ≡ a −1 (y − b) (mod 26) and so our \

Decipherment function is

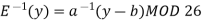
Q7) Decipher HPCCXAQ if the encipherment function is

A8)

We begin by finding the decipherment function. Since 5x ≡ 1 (mod 26) is solved with x ≡ 21 (mod 26) we see 5−1 (mod 26) = 21. Therefore,

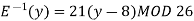
And so filling in our table gives

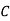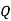	7	15	2	2	23	0	11
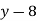	-1	7	-6	-6	15	-8	8
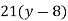	-2	147	-126	-126	315	-168	168
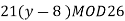	5	17	4	4	3	14	12

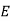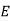Q8) Suppose that an affine cipher E(x) = (ax + b) MOD 26 enciphers H as X and Q as Y. Find the cipher (that is, determine a and b).

A9)

We see that

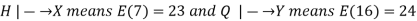
That is,

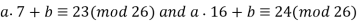
Subtracting gives 16a − 7a ≡ 1 (mod 26) so that 9a ≡ 1 (mod 26). Therefore, a = 9−1 (mod 26) = 3. Finally, we substitute a = 3 into either of the earlier equations and solve for b,

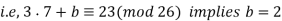
In summary,

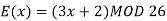
Q9) This example shows how we can encrypt plaintext 9 using the RSA public-key encryption algorithm. This example uses prime numbers 7 and 11 to generate the public and private keys.

A10)

Step 1: Select two large prime numbers, p, and q.

p = 7

q = 11

Step 2: Multiply these numbers to find n = p x q, where n is called the modulus for encryption and decryption.

First, we calculate

n = p x q

n = 7 x 11

n = 77

Step 3: Choose a number e less that n, such that n is relatively prime to (p - 1) x (q -1). It means that e and (p - 1) x (q - 1) have no common factor except 1. Choose "e" such that 1<e < φ (n), e is prime to φ (n), gcd (e, d (n)) =1.

Second, we calculate

φ (n) = (p - 1) x (q-1)

φ (n) = (7 - 1) x (11 - 1)

φ (n) = 6 x 10

φ (n) = 60

Let us now choose relative prime e of 60 as 7.

Thus the public key is <e, n> = (7, 77)

Step 4: A plaintext message m is encrypted using public key <e, n>. To find ciphertext from the plain text following formula is used to get ciphertext C.

To find ciphertext from the plain text following formula is used to get ciphertext C.

C = me mod n

C = 97 mod 77

C = 37

Step 5: The private key is <d, n>. To determine the private key, we use the following formula d such that:

De mod {(p - 1) x (q - 1)} = 1

7d mod 60 = 1, which gives d = 43

The private key is <d, n> = (43, 77)

Step 6: A ciphertext message c is decrypted using private key <d, n>. To calculate plain text m from the ciphertext c following formula is used to get plain text m.

m = cd mod n

m = 3743 mod 77

m = 9

In this example, Plain text = 9 and the ciphertext = 37

Q10) In an RSA cryptosystem, a particular A uses two prime numbers, 13 and 17, to generate the public and private keys. If the public of A is 35. Then the private key of A is ……………?.

A11)

Step 1: in the first step, select two large prime numbers, p and q.

p = 13

q = 17

Step 2: Multiply these numbers to find n = p x q, where n is called the modulus for encryption and decryption.

First, we calculate

n = p x q

n = 13 x 17

n = 221

Step 3: Choose a number e less that n, such that n is relatively prime to (p - 1) x (q -1). It means that e and (p - 1) x (q - 1) have no common factor except 1. Choose "e" such that 1<e < φ (n), e is prime to φ (n), gcd (e, d (n)) =1.

Second, we calculate

φ (n) = (p - 1) x (q-1)

φ (n) = (13 - 1) x (17 - 1)

φ (n) = 12 x 16

φ (n) = 192

g.c.d (35, 192) = 1

Step 3: To determine the private key, we use the following formula to calculate the d such that:

Calculate       d = de mod φ (n) = 1

d = d x 35 mod 192 = 1

d = (1 + k.φ (n))/e           [let k =0, 1, 2, 3………………]

Put k = 0

d = (1 + 0 x 192)/35

d = 1/35

Put k = 1

d = (1 + 1 x 192)/35

d = 193/35

Put k = 2

d = (1 + 2 x 192)/35

d = 385/35

d = 11

The private key is <d, n> = (11, 221)

Hence, private key i.e. d = 11

Q11) A RSA cryptosystem uses two prime numbers 3 and 13 to generate the public key= 3 and the private key = 7. What is the value of cipher text for a plain text?

A12)

Step 1: In the first step, select two large prime numbers, p and q.

p = 3

q = 13

Step 2: Multiply these numbers to find n = p x q, where n is called the modulus for encryption and decryption.

First, we calculate

n = p x q

n = 3 x 13

n = 39

Step 3: If n = p x q, then the public key is <e, n>. A plaintext message m is encrypted using public key <e, n>. Thus the public key is <e, n> = (3, 39).

To find ciphertext from the plain text following formula is used to get ciphertext C.

C = me mod n

C = 53 mod 39

C = 125 mod 39

C = 8

Q12) A RSA cryptosystem uses two prime numbers, 3 and 11, to generate private key = 7. What is the value of ciphertext for a plain text 5 using the RSA public-key encryption algorithm?

A13)

Step 1: in the first step, select two large prime numbers, p and q.

p = 3

q = 11

Step 2: Multiply these numbers to find n = p x q, where n is called the modulus for encryption and decryption.

First, we calculate

n = p x q

n = 3 x 11

n = 33

Step 3: Choose a number e less that n, such that n is relatively prime to (p - 1) x (q -1). It means that e and (p - 1) x (q - 1) have no common factor except 1. Choose "e" such that 1< e < φ (n), e is prime to φ (n), gcd (e, d (n)) =1.

Second, we calculate

φ (n) = (p - 1) x (q-1)

φ (n) = (3 - 1) x (11 - 1)

φ (n) = 2 x 10

φ (n) = 20

Step 4: To determine the public key, we use the following formula to calculate the d such that:

Calculate e x d = 1 mod φ (n)

e x 7 = 1 mod 20

e x 7 = 1 mod 20

e = (1 + k. φ (n))/ d              [let k =0, 1, 2, 3………………]

Put k = 0

e = (1 + 0 x 20) / 7

e = 1/7

Put k = 1

e = (1 + 1 x 20) / 7

e = 21/7

e = 3

The public key is <e, n> = (3, 33)

Hence, public key i.e. e = 3

Q13) In an RSA cryptosystem, a particular A uses two prime numbers p = 13 and q =17 to generate her public and private keys. If the public key of A is 35. Then the private key of A is?

A14)

1. 

2.  Compute n=13×17=221 and

3.  

4.   Compute d (private key)

5. 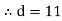   (private key)

Q14) Given the public information [n, e] = [2599, 73], find the decrypt key d.

A15)

First, we must factor 2599 into its two prime factors. We find that 2599=23⋅113. We now determine that ϕ(2599)=ϕ(23)ϕ(113)=(22)(112)=2464. Now we want to solve the following linear congruence:

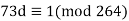
We can solve this linear congruence by finding a modular inverse of 73 (mod 2464) by the division algorithm as follows:

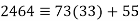
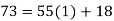
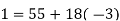
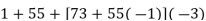
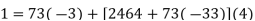
Hence -135 can be used as a modular inverse. We thus get that:

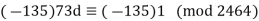
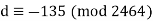
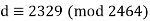
Hence our decryption key d = 2329.

Q15) Given the public information [n, e] = [2257, 997], find the decryption key d.

A16)

We will first factor 2257 into its two prime constituents. We note that 2257=37⋅61. We note calculate that ϕ(2257)=ϕ(37)ϕ(61)=(36)(60)=2160.

We now want to solve the linear congruence 997d≡1(mod2160). We can do this by finding a modular inverse of 997 (mod 2160) by the division algorithm as follows:

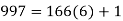
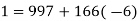
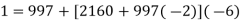
Hence we can use 13 as an inverse to 997 (mod 2160). It hence follows that:

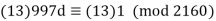
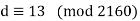
Q16) In an RSA cryptosystem, a particular A uses two prime numbers p = 13 and q =17 to generate her public and private keys. If the public key of A is 35. Then the private key of A is?

A17)

1.  and 
2. Compute  and 
3.  (public key)
4. Compute  (private key)

5. 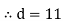   (private key)

Q17) Callie wants to send the message M = 13 to Alice. Using Alice’s public and private keys, calculate the ciphertext C, and the value for R when Alice recovers the message.

A18)

Callie encrypts message M = 13:

• Alice’s public key is (n, e) = (33, 3).
• When Me = 133 = 2197 is divided by 33, the remainder is C = 19.
• Callie sends to Alice ciphertext C = 19.

Alice receives and decrypts ciphertext C = 19:

• Alice uses her private key (n, d) = (33, 7).
• When 197 = 893, 871, 739 is divided by 33, the remainder is R = 13
• R = 13 = M, the original message from Callie!

Q18) With p = 23, q = 19, we have m = (p − 1)(q − 1) = 22(18) = 396. We want to find d so that ed = 283d has a remainder of 1 when divided by m = 396. One way to do this is by simple trial and error, increasing the value of d until 283d divided by 396 leaves a remainder of 1.

A19)

		Remainder when 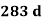is divided by 396
1 2 3 4 5 6 7	283 566 849 1132 1415 1698 1981	283 170 57 340 227 114 1

We see that d = 7 works; that is ed = 283 × 7 = 1981 leaves a remainder of 1 when divided by 396.

In general, trial and error could take a very long time, as the value of d could be a big number. Instead, an ancient technique called Euclid’s Algorithm can be used to find d in the linear Diophantine equation 283d + 396y = 1.