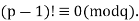Unit - 1
Linear Diophantine equation
Q1) What is Linear Diophantine Equation?
A1)
A Diophantine problem is one in which all of the answers must be integers. I'll use the word Diophantine equations to refer to equations that must be solved over the integers.
For example, the equation 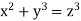 has many solutions over the reals. Here's a solution:
has many solutions over the reals. Here's a solution:

However, there are no nonzero integer solutions to this equation. Fermat's Last Theorem has a specific instance.
The following equation, on the other hand, has an endless number of integer solutions:

 and
and  are examples of solutions.
are examples of solutions.
In this section, I'll look at equations like the last one. They're called linear Diophantine equations.
Q2) Find the general solution to the following Diophantine equation.


A2)
Let 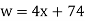
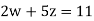
 and
and  is a particular solution. So
is a particular solution. So

Then
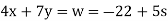
 and
and  is a particular solution. The general solution is
is a particular solution. The general solution is

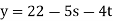

A general linear Diophantine equation has the form

There are solutions if  . If there is a solution, it will in general have
. If there is a solution, it will in general have  parameters --- exactly as you'd expect from linear algebra.
parameters --- exactly as you'd expect from linear algebra.
Here's the proof of the theorem for the two-variable case.
Proof. (two variable case) Consider the linear Diophantine equation

Case 1. Suppose 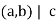 , . If x and y are solutions to the equation, then
, . If x and y are solutions to the equation, then
 .
.
This contradiction shows that there cannot be a solution.
Case 2. Suppose  . Write
. Write  for
for  . There are integers m and n such that
. There are integers m and n such that

Then
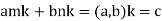
Hence,  ,
, 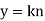 , is a solution.
, is a solution.
Suppose  ,
,  , is a particular solution. Then
, is a particular solution. Then

This proves that 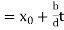 ,
,  is a solution for every
is a solution for every 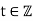
Finally, I want to show that every solution has this form. Suppose then that  is a solution. Then
is a solution. Then 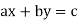 and
and  imply
imply
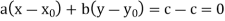
Therefore,


Now 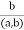 divides the left side, so it divides the right side. However,
divides the left side, so it divides the right side. However,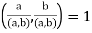 . Therefore,
. Therefore,

Thus,
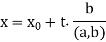
Substitute 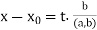 back into the last x-y equation above:
back into the last x-y equation above:
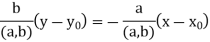
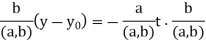
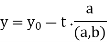
Thus,

Q3) State and Explain Prime Counting Function?
A3)
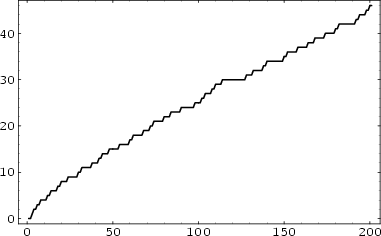
The function 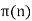 giving the number of Primes less than n (Shanks 1993, p. 15). The first few values are 0, 1, 2, 2, 3, 3, 4, 4, 4, 4, 5, 5, 6, 6, 6, ... (Sloane's A000720). The following table gives the values of
giving the number of Primes less than n (Shanks 1993, p. 15). The first few values are 0, 1, 2, 2, 3, 3, 4, 4, 4, 4, 5, 5, 6, 6, 6, ... (Sloane's A000720). The following table gives the values of  for powers of 10 (Sloane's A006880; Hardy and Wright 1979, p. 4; Shanks 1993, pp. 242-243; Ribenboim 1996, p. 237). Deleglise and Rivat (1996) have computed
for powers of 10 (Sloane's A006880; Hardy and Wright 1979, p. 4; Shanks 1993, pp. 242-243; Ribenboim 1996, p. 237). Deleglise and Rivat (1996) have computed 
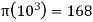




Q4) State and Explain Prime Number Theorem?
A4)
The prime number theorem is a formula that estimates the number of primes that are less than or equal to a given positive real number x. This number is usually written as (x), so (2) = 1, (3.5) = 2, and (10) = 4. The prime number theorem asserts that (x) is approximately equal to x/ln for high values of x. (x). For various values of x, the table compares the actual and projected number of primes.

The mathematical features of prime numbers were first studied by ancient Greek mathematicians. (Many people had previously examined such numbers for their mystical or spiritual properties.) While many people have remarked that primes appear to “thin out” as numbers get larger, Euclid may have been the first to prove that there is no biggest prime; in other words, there are an unlimited amount of primes in his Elements (c. 300 BC). Over the years that followed, mathematicians tried and failed to establish a formula that would allow them to generate an infinite number of primes. Others began to conjecture about formulas that could describe the general distribution of primes after failing to find an explicit formula. The prime number theorem was initially proposed in 1798 by French mathematician Adrien-Marie Legendre as a conjecture. Legendre claimed that x/(ln(x) 1.08366) is very close to x/(ln(x) 1.08366) if x is not more than 1,000,000, based on his analysis of a table of primes up to 1,000,000. (x). The prime number theorem, which states the result for constant 0, is essentially equal to this result for any constant, not simply 1.08366. However, it is now recognised that for relatively small x, the constant that offers the best approximation to (x) is 1.
In his notebook, maybe around 1800, the eminent German mathematician Carl Friedrich Gauss conjectured an equivalent of the prime number theorem. The theorem was not proved until 1896, when French mathematicians Jacques-Salomon Hadamard and Charles de la Valée Poussin separately demonstrated that the ratio x/ln(x) equals infinity in the limit (as x increases to infinity) (x).
Although the prime number theorem states that as x grows larger, the difference between (x) and x/ln(x) becomes vanishingly small in comparison to the magnitude of either of these numbers, one can still request an estimate of that difference. Square root of x ln is thought to be the best estimate of this discrepancy (x).
Q5) State and Explain GoldBach Conjecture?
A5)
"At least it seems that every integer bigger than 2 is the sum of three primes," Goldbach's original conjecture (also known as the "ternary" Goldbach conjecture) asserts in a June 7, 1742 letter to Euler (Goldbach 1742; Dickson 2005, p. 421). It's worth noting that Goldbach thought 1 to be a prime number, which is no longer the case. An equivalent form of this claim (known as the "strong" or "binary" Goldbach conjecture) asserts that all positive even numbers may be written as the sum of two primes, as re-stated by Euler. A Goldbach partition is a pair of primes that together form a positive integer (Oliveira e Silva).
"It is very easy to make good predictions," writes Hardy (1999, p. 19). "Indeed, there are theorems, like 'Goldbach's Theorem,' which have never been proved and which any fool could have guessed." Between March 20, 2000 and March 20, 2002, Faber and Faber offered a prize to anyone who could prove Goldbach's conjecture, but the prize went unclaimed, and the conjecture remains open.
Schnirelman (1939) proved that each even integer may be expressed as the sum of not more than primes (Dunham 1990), which appears to be a long way from a proof for two primes! Pogorzelski (1977) claimed to have proved the Goldbach conjecture, but his proof is widely regarded as insufficient (Shanks 1985). The bounds that have been demonstrated to be true for numbers so that the strong Goldbach conjecture is true are summarised in the table below.
Bound | Reference |
 | Desboves 1885 |
 | Pipping 1938 |
 | Stein and Stein 1965ab |
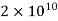 | Granville et al. 1989 |
 | Sinisalo 1993 |
 | Deshouillers et al. 1998 |
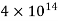 | Richstein 1999, 2001 |
 | Oliveira e Silva (Mar. 24, 2003) |
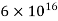 | Oliveira e Silva (Oct. 3, 2003) |
 | Oliveira e Silva (Feb. 5, 2005) |
 | Oliveira e Silva (Dec. 30, 2005) |
 | Oliveira e Silva (Jul. 14, 2008) |
 | Oliveira e Silva (Apr. 2012) |
The "weak" Goldbach conjecture states that all odd numbers are equal to the sum of three odd primes. Vinogradov (1937ab, 1954) proved that each sufficiently large odd number is the sum of three primes (Nagell 1951, p. 66; Guy 1994), and Estermann (1938) proved that practically all even numbers are the sums of two primes (Nagell 1951, p. 66; Guy 1994). "Sufficiently large" was Vinogradov's original phrase. 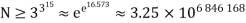 was subsequently reduced to
was subsequently reduced to  by Chen and Wang (1989). Chen (1973, 1978) further demonstrated that any sufficiently big even numbers are the product of at most two primes and the sum of a prime (Guy 1994, Courant and Robbins 1996). Helfgott proved the weak Goldbach conjecture more than two and a half centuries after the original guess was made (2013, 2014).
by Chen and Wang (1989). Chen (1973, 1978) further demonstrated that any sufficiently big even numbers are the product of at most two primes and the sum of a prime (Guy 1994, Courant and Robbins 1996). Helfgott proved the weak Goldbach conjecture more than two and a half centuries after the original guess was made (2013, 2014).
Levy's conjecture is a stronger variant of the weak hypothesis, stating that any odd number may be written as the sum of a prime plus twice a prime.
The Goldbach conjecture's corresponding statement is that there are primes and such for every positive integer.
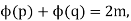
|
Where 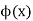 is the totient function (e.g., Havil 2003, p. 115; Guy 2004, p. 160). (This follows immediately from
is the totient function (e.g., Havil 2003, p. 115; Guy 2004, p. 160). (This follows immediately from 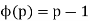 for p prime.) Erdős and Moser have considered dropping the restriction that p and q be prime in this equation as a possibly easier way of determining if such numbers always exist (Guy 1994, p. 105).
for p prime.) Erdős and Moser have considered dropping the restriction that p and q be prime in this equation as a possibly easier way of determining if such numbers always exist (Guy 1994, p. 105).
Other variants of the Goldbach conjecture include the statements that every even number  is the sum of two odd primes, and every integer >17 the sum of exactly three distinct primes.
is the sum of two odd primes, and every integer >17 the sum of exactly three distinct primes.
Let  be the number of representations of an even number n as the sum of two primes. Then the "extended" Goldbach conjecture states that
be the number of representations of an even number n as the sum of two primes. Then the "extended" Goldbach conjecture states that

Where  is the twin primes constant.
is the twin primes constant.
Q6) What are Linear Congruences?
A6)
A linear congruence equation
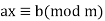 (1)
(1)
Is solvable iff the congruence
 (2)
(2)
With 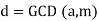 is the greatest common divisor is solvable. Let one solution to the original equation be
is the greatest common divisor is solvable. Let one solution to the original equation be  . Then the solutions are
. Then the solutions are 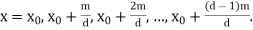 If
If  , then there is only one solution <m.
, then there is only one solution <m.
The solution of a linear congruence can be found in the Wolfram Language using Reduce[a*x == b, x, Modulus -> m].
Finding the value of a fractional congruence, for which a greedy-type solution exists, is comparable to solving a linear congruence problem. (1), for example, can be rewritten as
 (3)
(3)
Which can also be written
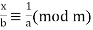 (4)
(4)
The answer can be found as Mod[b y, m] of the PowerMod[a,, m] solution produced by the Wolfram Language function. A modular inverse is what this is called.
Two or more linear congruences occur at the same time.
 (5)
(5)
 (6)
(6)
Are solvable using the Chinese remainder theorem.
Q7) State and Explain Chinese Remainder Theorem?
A7)
Let r and s be positive integers which are relatively prime and let a and b be any two integers. Then there is an integer N such that
 (1)
(1)
And
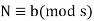 (2)
(2)
Moreover, N is uniquely determined modulo r s. An equivalent statement is that if 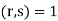 , then every pair of residue classes modulo r and s corresponds to a simple residue class modulo r s.
, then every pair of residue classes modulo r and s corresponds to a simple residue class modulo r s.
The Chinese remainder theorem is implemented in the Wolfram Language as Chinese Remainder {a1, a2, ...} {m1, m2, ...}. Reduce in with an Integers domain specification is also used to apply the Chinese remainder theorem indirectly.
The following is a generalisation of the theorem. Given a set of congruences that occur at the same time,
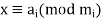 (3)
(3)
For  and for which the
and for which the 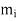 are pairwise relatively prime, the solution of the set of congruences is
are pairwise relatively prime, the solution of the set of congruences is
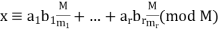 (4)
(4)
Where
 (5)
(5)
And the 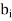 are determined from
are determined from
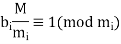
Q8) Explain Fermat little theorem?
A8)
If p is a prime number and a is a natural number, then
 (1)
(1)
Furthermore, if  (p does not divide a), then there exists some smallest exponent d such that
(p does not divide a), then there exists some smallest exponent d such that
 (2)
(2)
And d divides p-1. Hence,
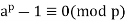
 (3)
(3)
The theorem is sometimes also simply known as "Fermat's theorem" (Hardy and Wright 1979, p. 63).
This is a specific example of Euler's totient theorem and a generalisation of the Chinese hypothesis. It's also known as Fermat's primality test, and it's a required but insufficient test for primality. The first proof was published by Euler in 1749, despite the fact that it was apparently proved (but suppressed) by Fermat. The term "Fermat's small theorem" was initially used to characterise the theorem in a German textbook by Hensel (1913), and it also appears in Mac Lane (1940) and Kaplansky (1941). (1945).
The theorem is easily proved using mathematical induction on  . Suppose
. Suppose  (i.e.,
(i.e.,  divides
divides  ). Then examine
). Then examine
 (4)
(4)
From the binomial theorem,
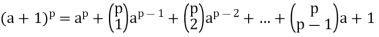
Rewriting,
 (6)
(6)
But p divides the right side, so it also divides the left side. Combining with the induction hypothesis gives that p divides the sum
 (7)
(7)
Assume that the hypothesis is correct for any. Fermat's simple theorem is another name for the theorem. Wilson's theorem follows Fermat's small theorem as a corollary.
Fermat's little theorem shows that, if  is prime, there does not exist a base
is prime, there does not exist a base 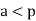 with
with 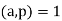 such that
such that  possesses a nonzero residue modulo p. If such base a exists, p is therefore guaranteed to be composite. However, the lack of a nonzero residue in Fermat's little theorem does not guarantee that p is prime. Fermat's little theorem is frequently referred to as the Fermat compositeness test since it has the property of indisputably certifying composite numbers while passing some primes. A probable prime is a number that fulfils Fermat's little theorem for some nontrivial base and is not known to be composite.
possesses a nonzero residue modulo p. If such base a exists, p is therefore guaranteed to be composite. However, the lack of a nonzero residue in Fermat's little theorem does not guarantee that p is prime. Fermat's little theorem is frequently referred to as the Fermat compositeness test since it has the property of indisputably certifying composite numbers while passing some primes. A probable prime is a number that fulfils Fermat's little theorem for some nontrivial base and is not known to be composite.
Fermat pseudoprimes (or simply "pseudoprimes") are composite numbers that have zero residue for some s and hence are not identified as composite. Worse still, there exist numbers known as Carmichael numbers (the smallest of which is 561) which give zero residue for any choice of the base a relatively prime to p. However, Fermat's little theorem converse provides a criterion for certifying the primality of a number. A table of the smallest pseudoprimes 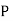 for the first 100 bases
for the first 100 bases  follows (OEIS A007535; Beiler 1966, p. 42 with typos corrected).
follows (OEIS A007535; Beiler 1966, p. 42 with typos corrected).
 |  |  |  | 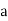 |  |  |  |  |  |
2 | 341 | 22 | 69 | 42 | 205 | 62 | 63 | 82 | 91 |
3 | 91 | 23 | 33 | 43 | 77 | 63 | 341 | 83 | 105 |
4 | 15 | 24 | 25 | 44 | 45 | 64 | 65 | 84 | 85 |
5 | 124 | 25 | 28 | 45 | 76 | 65 | 112 | 85 | 129 |
6 | 35 | 26 | 27 | 46 | 133 | 66 | 91 | 86 | 87 |
7 | 25 | 27 | 65 | 47 | 65 | 67 | 85 | 87 | 91 |
8 | 9 | 28 | 45 | 48 | 49 | 68 | 69 | 88 | 91 |
9 | 28 | 29 | 35 | 49 | 66 | 69 | 85 | 89 | 99 |
10 | 33 | 30 | 49 | 50 | 51 | 70 | 169 | 90 | 91 |
11 | 15 | 31 | 49 | 51 | 65 | 71 | 105 | 91 | 115 |
12 | 65 | 32 | 33 | 52 | 85 | 72 | 85 | 92 | 93 |
13 | 21 | 33 | 85 | 53 | 65 | 73 | 111 | 93 | 301 |
14 | 15 | 34 | 35 | 54 | 55 | 74 | 75 | 94 | 95 |
15 | 341 | 35 | 51 | 55 | 63 | 75 | 91 | 95 | 141 |
16 | 51 | 36 | 91 | 56 | 57 | 76 | 77 | 96 | 133 |
17 | 45 | 37 | 45 | 57 | 65 | 77 | 247 | 97 | 105 |
18 | 25 | 38 | 39 | 58 | 133 | 78 | 341 | 98 | 99 |
19 | 45 | 39 | 95 | 59 | 87 | 79 | 91 | 99 | 145 |
20 | 21 | 40 | 91 | 60 | 341 | 80 | 81 | 100 | 153 |
21 | 55 | 41 | 105 | 61 | 91 | 81 | 85 |
|
|
Q9) State and Explain Wilson Theorem?
A9)
Iff  is a prime, then
is a prime, then  is a multiple of
is a multiple of  , that is
, that is
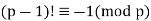 (1)
(1)
Although it was previously known to Leibniz, this theorem was proposed by John Wilson and published by Waring (1770). Lagrange demonstrated it in 1773. Wilson's theorem, unlike Fermat's small theorem, is both necessary and sufficient for primality. When calculating a composite number,  except when
except when  .
.
A corollary to the theorem states that iff a prime p is of the form 4k+1, then
 (2)
(2)
The first few primes of the form 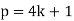 are
are 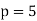 , 13, 17, 29, 37, 41, ... (OEIS A002144), corresponding to k=1, 3, 4, 7, 9, 10, 13, 15, 18, 22, 24, 25, 27, 28, 34, 37, ... (OEIS A005098).
, 13, 17, 29, 37, 41, ... (OEIS A002144), corresponding to k=1, 3, 4, 7, 9, 10, 13, 15, 18, 22, 24, 25, 27, 28, 34, 37, ... (OEIS A005098).
Gauss's generalization of Wilson's theorem considers P(n) the product of integers that are less than or equal to and relatively prime to an integer n. For n=1, 2, ..., the first few values are 1, 1, 2, 3, 24, 5, 720, 105, 2240, 189, ... (OEIS A001783). Then defining
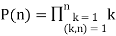 (3)
(3)
Gives the congruence

For p an odd prime. When n=2, this reduces to P which is equivalent to  . The first few values of
. The first few values of  are 0, -1, -1, -1, -1,-1,-1, 1,-1, -1 -1, ... (OEIS A103131).
are 0, -1, -1, -1, -1,-1,-1, 1,-1, -1 -1, ... (OEIS A103131).
Szántó (2005) notes that defining
 (5)
(5)
 (6)
(6)
Then, taking the minimal residue,
 (7)
(7)
For  the first terms are then 0, -1, 1, 1, 0,-1, 1, 0, -1, -1, 0, ...
the first terms are then 0, -1, 1, 1, 0,-1, 1, 0, -1, -1, 0, ...
Q10) State the theorem for Diophantine Equation?
A10)
Let 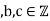 . Consider the Diophantine equation
. Consider the Diophantine equation
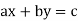
(a) If 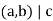 , there are no solutions.
, there are no solutions.
(b) If  , there are infinitely many solutions of the form
, there are infinitely many solutions of the form
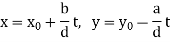
Here  is a particular solution, and
is a particular solution, and 
If you've had a course in differential equations, you may have seen something like this. 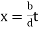 and
and  give a general solution to the homogeneous equation
give a general solution to the homogeneous equation

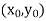 is a particular solution to
is a particular solution to  . Their sum gives a general solution to the given (nonhomogeneous) equation.
. Their sum gives a general solution to the given (nonhomogeneous) equation.
Before I give the proof, I'll give some examples, and also discuss the three variable equation 
Q11) Using the Prime Number Theorem, estimate the number of prime numbers between 2 million and 7 million.
A11)
The number of primes between 2000000 and 7000000
= π(7000000) − π(1999999)
≈ 7000000/ log(7000000) − 1999999/ log(1999999)
≈ 306274.
The exact answer is 327715, so we are about 6.5% out.
Q12) Calculate ϕ(n) for n = 1200 and n = 2008.
A12)


Q13) Let n ∈ N and let p be a prime. Show that if p | n then ϕ(np) = pϕ(n). Hint: consider the prime factorization of n.
A13)
Since p | n, the prime factorization of n is
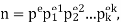
For some k. Thus

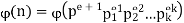

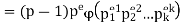

Q14) Solve 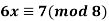 .
.
A14)
Since 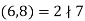 , there are no solutions.
, there are no solutions.
Q15) Solve 
A15)
Since  , there will be 1 solutions mod 4. I'll find it in three different ways.
, there will be 1 solutions mod 4. I'll find it in three different ways.
Using Diophantine equations that are linear.
 implies 3x+4y=7 for some y.
implies 3x+4y=7 for some y.
By inspection  ,
,  is a particular solution.
is a particular solution.  , so the general solution is
, so the general solution is

The y equation has no bearing. According to the x equation,

Using the Euclidean algorithm. Since 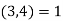 , some linear combination of 3 and 4 is equal to 1. In fact,
, some linear combination of 3 and 4 is equal to 1. In fact, 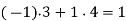
This tells me how to juggle the coefficient of x to get 1 x :

(I used the fact that 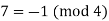 .
.
Here is a multiplication table with inverses mod 4:
* | 0 | 1 | 2 | 3 |
0 | 0 | 0 | 0 | 0 |
1 | 0 | 1 | 2 | 3 |
2 | 0 | 2 | 0 | 2 |
3 | 0 | 3 | 2 | 1 |
I see that 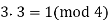 , so I multiply the equation by 3:
, so I multiply the equation by 3:

Q16) Solve 
A16)
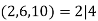 , so there are
, so there are 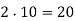 solutions mod 10. I'll solve the equation using a reduction trick similar to the one I used to solve two variable linear Diophantine equations.
solutions mod 10. I'll solve the equation using a reduction trick similar to the one I used to solve two variable linear Diophantine equations.
The following equation is the same as 
Set 
Then 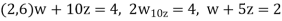
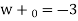 ,
,  , is a particular solution. The general solution is
, is a particular solution. The general solution is

Substitute for w:
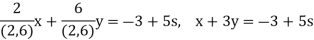
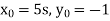 , is a particular solution. The general solution is
, is a particular solution. The general solution is

 will produce distinct values of y mod 10. Note, however, that s and
will produce distinct values of y mod 10. Note, however, that s and 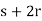 produce
produce  and
and 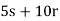 , which are congruent mod 10. That is, adding a multiple of 2 to a given value of s makes the
, which are congruent mod 10. That is, adding a multiple of 2 to a given value of s makes the 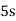 term in x repeat itself mod 10. So I can get all possibilities for x mod 10 by letting
term in x repeat itself mod 10. So I can get all possibilities for x mod 10 by letting 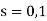 .
.
All together, the distinct solutions mod 10 are
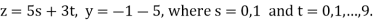
Q17) Find all solutions of x2 ≡ 1 (mod 144).
A17)
Two simultaneous congruences can be used to replace our congruence:
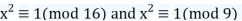
X2 ≡ 1 (mod 16) has 4 solutions: x ≡ ±1 or ±7 (mod 16)
x 2 ≡ 1 (mod 9) has 2 solutions: x ≡ ±1 (mod 9)
There are 8 alternatives:


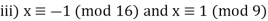
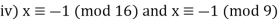

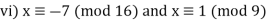
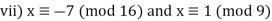

With k = 2, m1 = 16, and m2 = 9, each case above has a unique solution for x modulo 144, according to the Chinese Remainder Theorem.
We arrive at the following conclusion:

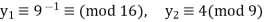

The following are the eight options:





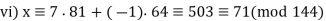
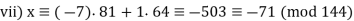
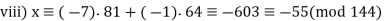
Q18) Calculate  mod 11 efficiently using Fermat’s Little Theorem. Solution. The number 2 is not divisible by the prime 11, so
mod 11 efficiently using Fermat’s Little Theorem. Solution. The number 2 is not divisible by the prime 11, so
A18)
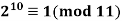
By Fermat’s Little Theorem. According to the division algorithm,

Since
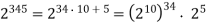
Then,
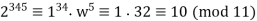
Thus,

The following corollary to Fermat's Little Theorem is actually required for RSA encryption.
Q19) Show that the inverse of 5 modulo 101 is 599
A19)
5 100 ≡ 1 (mod 101),
So
5 99 · 5 ≡ 5 · 5 99 ≡ 1 (mod 101),
Which by definition means that 599 is the inverse of 5 modulo 101.
Q20) Use repeated squaring to simplify 599 (mod 101).
A20)


Thus




Q21) Hence solve the equation  (mod 101).
(mod 101).
A21)
x ≡ 5 −1 · 31 ≡ 81 · 31 ≡ 87 (mod 101).
Check:
5 · 87 = 435 ≡ 31 (mod 101).
Q22) Find the two smallest positive integer solutions to the following system of equivalences
x ≡ 2 (mod 5)
x ≡ 5 (mod 8)
x ≡ 4 (mod 37)
A22)
This is a direct application of the CRT: We have m1 = 5, m2 = 8, m3 = 37, so
M1 = 8 · 37 = 296 M2 = 5 · 37 = 185 M3 = 5 · 8 = 40
M1 ≡ 1 (mod 5) M2 ≡ 1 (mod 8) M3 ≡ 3 (mod 37)
We have 1 · 1 ≡ 1 (mod 5) 1 · 1 ≡ 1 (mod 8) 3 · 25 ≡ 1 (mod 37),
So N1 = 1, N2 = 1, N3 = 25,
Thus x ≡ 2 · 296 · 1 + 5 · 185 · 1 + 4 · 40 · 25 = 5517 ≡ 1077 (mod 5 · 8 · 37). An integer satisfies the system of congruences if it is in this congruence class modulo 5 · 8 · 37 = 1480. The two smallest positive integers in this congruence class are 1077 and 2557.
Q23) Find the remainder of 97! when divided by 101.
A23)
First we will apply Wilson's theorem to note that 100!≡−1(mod101). When we decompose the factorial, we get that:

Now we can see that 1001(mod101), 992(mod101), and 983 are all mod101 (mod101). Hence:


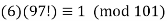 ……….(2)
……….(2)
Now we want to find a modular inverse of 6 (mod 101). Using the division procedure, we arrive to the following:


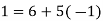

 ……………..(3)
……………..(3)
As a result, 17 can be used as the inverse of 6. (mod 101). The following is the result:
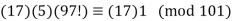
 ……………(4)
……………(4)
Hence, 97! has a remainder of 17 when divided by 101.
Q24) Find the remainder of 67! when divided by 71.
A24)
Using Wilson's theorem, we have that 70!≡−1(mod71). Decomposing the factorial we get that:

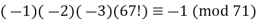

 …………..(5)
…………..(5)
Let's use the division procedure to obtain the modular inverse of 6 (mod 71).:



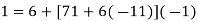
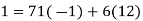 ……………………(6)
……………………(6)
As a result, 12 can be used as the inverse. Thus:
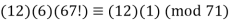
 …………………(7)
…………………(7)
Hence when 67! is divided by 71, the remainder leftover is 12.
Q25) Find the remainder of 53! when divided by 61.
A25)
We know that by Wilson's theorem 60!≡−1(mod61). Decomposing 60!, we get that:



 …….……(8)
…….……(8)
To find a modular inverse of 52 (mod 61), we'll utilise the division algorithm:


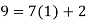
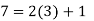
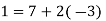




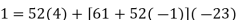
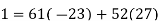 ……………….(9)
……………….(9)
As a result, 27 can be used as the inverse (mod 61). As a result, we have:

 ………………….(10)
………………….(10)
Q26) What is the remainder of 149! when divided by 139?
A26)
From Wilson's theorem we know that 138!≡−1(mod139). We are now going to multiply both sides of the congruence until we get up to 149!:



Hence the remainder of 149! when divided by 139 is 0.
In fact, this should make sense, since 149! = 149 x 148 x … x 139 x 138 x … x 2 x 1. For any primes p and q where  , it follows that
, it follows that