Unit - 3
Order of an integer modulo
Q1) How to find Order of an integer Modulo n?
A1)
You may see strange consequences when you exponentiate an integer number modulo another integer number. 33 = 27 = 12 mod 15, for example, whereas 34 = 81 = 6 mod 15. That is, multiplying 12 by 3 modulo 15 produces a result that is less than 12!? Alternatively, if you multiply 33 by 24 (the amount of hours in a day), you get 33 = 27 = 3 mod 24.
You can even discover a power r such that mr = 1 mod n for some values m > 1. We have 42 = 16 = 1 mod 15 as an example.
The order is defined as the smallest positive integer power r of an integer m modulo a (natural) number n.
mr = 1 mod n.
The order r of m modulo n is shortly denoted by ordn(m). For some constellations, however, there does not exists any positive power. Above we saw, e.g., that 33 = 3 mod 24, i.e., 33 = 31 mod 24, and moreover we directly compute 32 = 34 = 9 mod 24. Hence, any even power of 3 yields 9 modulo 24, and any odd power of 3 is 3 modulo 24.
Worse, there are situations when numbers with a positive power vanish. Take a look at 122 = 144 = 0 mod 24 as an example. There is no positive finite power to provide the order of such numbers, hence the order is specified as infinite.
If n is prime, then any integer that is relatively prime to n has a finite order, according to group theory. For example, if n = 7, the following table can be used to determine the order of any integer m.
m | 1 | 2 | 3 | 4 | 5 | 6 | 8 | ... |
Ord7(m) | 1 | 3 | 6 | 3 | 6 | 2 | 1 | ... |
The dots (...) represent the fact that anything repeats cyclically. Check it out! More generally, any number m being prime relatively to n has a finite order with respect to n, e.g., for n=15,
m | 1 | 2 | 4 | 7 | 8 | 11 | 13 | 14 |
Ord15(m) | 1 | 4 | 2 | 4 | 4 | 2 | 4 | 2 |
The conceivable finite orders modulo n are divisors of the Carmichael function value, and vice versa, any divisor is at least one integer's order. The Carmichael function returns 4 for 15. In fact, in the table above, all divisors of 4 (specifically 1, 2, and 4) may be found as order values! You can use an applet to calculate the order.
Q2) How to find primitive roots for primes?
A2)
A primitive root of a prime  is an integer
is an integer  such that
such that 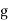 (mod
(mod 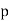 ) has multiplicative order
) has multiplicative order 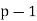 (Ribenboim 1996, p. 22). More generally, if
(Ribenboim 1996, p. 22). More generally, if  (
( and
and  are relatively prime) and
are relatively prime) and  is of multiplicative order
is of multiplicative order  modulo
modulo 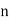 where
where 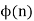 is the totient function, then
is the totient function, then  is a primitive root of
is a primitive root of 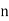 (Burton 1989, p. 187). The first definition is a special case of the second since
(Burton 1989, p. 187). The first definition is a special case of the second since  for
for  a prime.
a prime.
A primitive root of a number  (but not necessarily the smallest primitive root for composite
(but not necessarily the smallest primitive root for composite 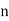 ) can be computed in the Wolfram Language using PrimitiveRoot[n].
) can be computed in the Wolfram Language using PrimitiveRoot[n].
If  has a primitive root, then it has exactly
has a primitive root, then it has exactly  of them (Burton 1989, p. 188), which means that if
of them (Burton 1989, p. 188), which means that if 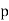 is a prime number, then there are exactly
is a prime number, then there are exactly 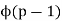 incongruent primitive roots of
incongruent primitive roots of 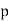 (Burton 1989). For
(Burton 1989). For 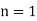 , 2, ..., the first few values of are 1, 1, 1, 1, 2, 1, 2, 2, 2, 2, 4, 2, 4, 2, 4, 4, 8, ... (OEIS A010554). n has a primitive root if it is of the form 2, 4,
, 2, ..., the first few values of are 1, 1, 1, 1, 2, 1, 2, 2, 2, 2, 4, 2, 4, 2, 4, 4, 8, ... (OEIS A010554). n has a primitive root if it is of the form 2, 4,  , or
, or 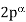 , where
, where  is an odd prime and
is an odd prime and  (Burton 1989, p. 204). The first few
(Burton 1989, p. 204). The first few  for which primitive roots exist are 2, 3, 4, 5, 6, 7, 9, 10, 11, 13, 14, 17, 18, 19, 22, ... (OEIS A033948), so the number of primitive root of order
for which primitive roots exist are 2, 3, 4, 5, 6, 7, 9, 10, 11, 13, 14, 17, 18, 19, 22, ... (OEIS A033948), so the number of primitive root of order 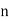 for
for 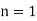 , 2, ... Are 0, 1, 1, 1, 2, 1, 2, 0, 2, 2, 4, 0, 4, ... (OEIS A046144).
, 2, ... Are 0, 1, 1, 1, 2, 1, 2, 0, 2, 2, 4, 0, 4, ... (OEIS A046144).
The smallest primitive roots for the first few primes  are 1, 2, 2, 3, 2, 2, 3, 2, 5, 2, 3, 2, 6, 3, 5, 2, 2, 2, ... (OEIS A001918). Here is table of the primitive roots for the first few n for which a primitive root exists (OEIS A046147).
are 1, 2, 2, 3, 2, 2, 3, 2, 5, 2, 3, 2, 6, 3, 5, 2, 2, 2, ... (OEIS A001918). Here is table of the primitive roots for the first few n for which a primitive root exists (OEIS A046147).
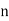 |  |
2 | 1 |
3 | 2 |
4 | 3 |
5 | 2, 3 |
6 | 5 |
7 | 3, 5 |
9 | 2, 5 |
10 | 3, 7 |
11 | 2, 6, 7, 8 |
13 | 2, 6, 7, 11 |
The largest primitive roots for 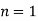 , 2, ..., are 0, 1, 2, 3, 3, 5, 5, 0, 5, 7, 8, 0, 11, ... (OEIS A046146). The smallest primitive roots for the first few integers n are given in the following table (OEIS A046145), which omits
, 2, ..., are 0, 1, 2, 3, 3, 5, 5, 0, 5, 7, 8, 0, 11, ... (OEIS A046146). The smallest primitive roots for the first few integers n are given in the following table (OEIS A046145), which omits 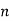 when
when  does not exist.
does not exist.
2 | 1 | 38 | 3 | 94 | 5 | 158 | 3 |
3 | 2 | 41 | 6 | 97 | 5 | 162 | 5 |
4 | 3 | 43 | 3 | 98 | 3 | 163 | 2 |
5 | 2 | 46 | 5 | 101 | 2 | 166 | 5 |
6 | 5 | 47 | 5 | 103 | 5 | 167 | 5 |
7 | 3 | 49 | 3 | 106 | 3 | 169 | 2 |
9 | 2 | 50 | 3 | 107 | 2 | 173 | 2 |
10 | 3 | 53 | 2 | 109 | 6 | 178 | 3 |
11 | 2 | 54 | 5 | 113 | 3 | 179 | 2 |
13 | 2 | 58 | 3 | 118 | 11 | 181 | 2 |
14 | 3 | 59 | 2 | 121 | 2 | 191 | 19 |
17 | 3 | 61 | 2 | 122 | 7 | 193 | 5 |
18 | 5 | 62 | 3 | 125 | 2 | 194 | 5 |
19 | 2 | 67 | 2 | 127 | 3 | 197 | 2 |
22 | 7 | 71 | 7 | 131 | 2 | 199 | 3 |
23 | 5 | 73 | 5 | 134 | 7 | 202 | 3 |
25 | 2 | 74 | 5 | 137 | 3 | 206 | 5 |
26 | 7 | 79 | 3 | 139 | 2 | 211 | 2 |
27 | 2 | 81 | 2 | 142 | 7 | 214 | 5 |
29 | 2 | 82 | 7 | 146 | 5 | 218 | 11 |
31 | 3 | 83 | 2 | 149 | 2 | 223 | 3 |
34 | 3 | 86 | 3 | 151 | 6 | 226 | 3 |
Q3) Explain composite number having primitive roots.
A3)
We now know when a prime number has a primitive root (it always does) and how many there are ((p 1)). What about the concept of composite numbers?
Let's start with the most basic type of composite number: prime powers.
6.33 is a lemma. Allow p to be an odd prime with r as the primitive root. Then either r or r + p modulo p 2 is a primitive root.
6.34 remark Since p + r is a primitive root modulo p, this suggests that there is some number that is a primitive root modulo p and also modulo p 2.
Proof. We know that ordp r = φ(p) = p − 1. Let n = ordp 2 r. By definition r n ≡ 1 mod p 2 , and thus r n ≡ 1 mod p. This implies that p − 1 = ordp r|n.
But we know that ordp 2 r|φ(p 2 ) = p(p − 1), so we have p − 1|n|p(p − 1). Thus either n = p − 1 or n = p(p − 1). If n = p(p − 1) then r is a primitive root modulo p 2 ; so suppose n = p − 1.
Let s = r + p. Then since s is also a primitive root modulo p, by the same logic we know that ordp 2 s is either p − 1 or p(p − 1). We wish to show that ordp 2 s 6= p − 1.
By the binomial theorem, we compute
s p−1 = (r + p) p−1 = X p−1 i=0 p − 1 i p i r p−1−i
= r p−1 + (p − 1)prp−2 + · · · + (p − 1)p p−2 r + p p−1
≡ r p−1 + (p − 1)prp−2 mod p 2
≡ 1 + (p − 1)prp−2 mod p 2 .
But since p6 |r we see that (p − 1)prp−2 6≡ 0 mod p 2 so s p−1 6≡ 1 mod p 2 as desired.
Thus ordp 2 s 6= p − 1, and the only remaining possibility is that ordp 2 s = p(p − 1) = φ(p 2 ).
Lemma 6.37. Let p be an odd prime. Then p k has a primitive root for any k ∈ N. Moreover, if r is a primitive root modulo p 2, then r is a primitive root modulo p k for any k ∈ N.
Proof. By lemma 6.33 we know that p has a primitive root r that is also a primitive root modulo p 2, and thus r p−1 6≡ 1 mod p 2.
First we will prove by induction that r p k−2 (p−1) 6≡ 1 mod p k for any k ≥ 2. The base case when k = 2 follows from Lemma 6.33. Suppose the assertion is true for k, and we will prove it for k + 1.
By inductive hypothesis, we know that
r p k−2 (p−1) 6≡ 1 mod p k.
But also (r, p) = 1 since r is a primitive root, and thus (r, pk−1 ) = 1. Thus φ(p k−1 ) = p k−2 (p − 1)
And thus r p k−2 (p−1) = r φ(p k−1 ) ≡ 1 mod p k−1 .
Thus we can find some integer such that
r p k−2 (p−1) = 1 + dpk−1
Because the congruence would hold modulo p k otherwise, p6 |d is used. Both sides of this can be raised to the pth power, which produces
r p k−2 (p−1)(p) = X p i=0 p i (dp) (k−1)i
r p k−1 (p−1) = 1 + dpk + p k+1 (stuff)
r p k−1 (p−1) ≡ 1 + dpk mod p k+1
≡ 1 mod p k+1
Since p6 |d. Thus by induction, for any k ≥ 2 we have
r p k−1 (p−1) 6≡ 1 mod p k+1 .
Now we wish to show that r is a primitive root modulo p k. Let n = ordp k r. We know that n|φ(p k ) = p k−1 (p − 1). Further, we know that ordp r = p − 1 so we must have p − 1|n. So n = p t (p − 1) for some 0 ≤ t ≤ k − 1.
But we know that
r p k−2 (p−1) 6≡ 1 mod p k ,
So we must have t < k − 2. Thus t = k − 1 and so ordr = p k−1 (p − 1) = φ(p k ), and r is a primitive root modulo p k .
Q4) Explain Euler’s criterion.
A4)
The congruence a(p1)/2(ap)(modp) holds if an integer an is not divisible by a prime number p>2, where (ap) is the Legendre symbol. Thus, the Euler criterion specifies that a number a0(modp) must be a quadratic residue or non-residue modulo p.
Euler also came up with a more general conclusion: If and only if, a number a0(modp) is a power residue of degree n modulo a prime number p.
a(p−1)/δ≡1(modp)
Where δ=hcf(p−1,n)
Both these assertions carry over easily to the case of a finite field.
Theorem 1 (Euler’s Criterion).
Let  be an odd prime. Let
be an odd prime. Let  be an integer that is relatively prime to
be an integer that is relatively prime to 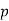 . Then the integer
. Then the integer  is a quadratic residue modulo
is a quadratic residue modulo 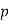 if and only if
if and only if 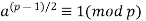 . On the other hand, the integer
. On the other hand, the integer 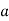 is a quadratic nonresidue modulo p if and only if
is a quadratic nonresidue modulo p if and only if  .
.
The task of determining the status of quadratic residue, according to Euler's Criterion, is as simple as completing a modular exponentiation. This can be done with modular arithmetic software or a calculator. The rapid powering approach can also be used to programme the exponentiation if desired.
Though Euler's Criterion (together with a calculator for modular arithmetic) is a foolproof method of determining the status of quadratic residues, the rule of quadratic reciprocity can make the process even easier. As the examples below indicate, applying the rule of reciprocity to check the status of quadratic residues may not need any modular exponentiation at all, and if it is, it is of a significantly lower scale.
Euler's Criterion also provides us with a number of fundamental truths concerning quadratic residues.
Theorem 2
Let 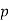 be an odd prime. The following properties are true:
be an odd prime. The following properties are true:
- If
 and
and 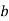 are both residues modulo
are both residues modulo  , then the product
, then the product  is a residue modulo
is a residue modulo 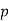 .
. - If If
 and
and 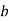 are both nonresidues modulo
are both nonresidues modulo  , then the product
, then the product  is a residue modulo
is a residue modulo  .
. - If
 and
and  are such that one of them is a residue modulo
are such that one of them is a residue modulo 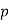 and the other is a nonresidue modulo
and the other is a nonresidue modulo 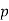 , then the product
, then the product  is a nonresidue modulo
is a nonresidue modulo 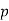 .
.
Theorem 2 says that the product of two integers of the same types (both residues or both nonresidues) is always a residue modulo the odd prime  . The product of two integers of different types is always a nonresidue modulo the odd prime
. The product of two integers of different types is always a nonresidue modulo the odd prime 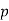 . The theorem follows from Euler’s criterion and from the fact that
. The theorem follows from Euler’s criterion and from the fact that  .
.
In arithmetic modulo a prime p, there exists a primitive root modulo  and that any primitive root generates by powering all the integers that are relatively prime to the modulus
and that any primitive root generates by powering all the integers that are relatively prime to the modulus  . Let
. Let  be a primitive root modulo an odd prime
be a primitive root modulo an odd prime  . It then follows that the quadratic residues modulo
. It then follows that the quadratic residues modulo 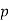 are the even powers of
are the even powers of  and the nonresidues are the odd powers of . A related fact is that when
and the nonresidues are the odd powers of . A related fact is that when 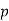 is an odd prime and when
is an odd prime and when 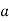 and
and 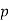 are relatively prime, the equation
are relatively prime, the equation  either has two solutions or has no solutions.
either has two solutions or has no solutions.
Theorem 3
Let  be a primitive root modulo an odd prime
be a primitive root modulo an odd prime 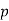 . For any
. For any  that is relatively prime to
that is relatively prime to 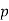 , the following is true:
, the following is true:
 is a quadratic residue modulo
is a quadratic residue modulo  if and only if
if and only if  is of the form
is of the form 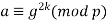 for some positive integer
for some positive integer  ,
, is a quadratic nonresidue modulo
is a quadratic nonresidue modulo 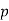 if and only if
if and only if  is of the form
is of the form 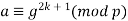 for some positive integer
for some positive integer 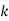 .
.
Q5) Explain the Legendre symbol?
A5)
The Legendre symbol is 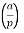 where the bottom argument is always an odd prime and the top argument can be any integer. When
where the bottom argument is always an odd prime and the top argument can be any integer. When 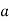 is an integer that is relatively prime to the odd prime
is an integer that is relatively prime to the odd prime 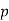 , the Legendre symbol
, the Legendre symbol  carries information on whether the integer
carries information on whether the integer  is quadratic residue modulo p. The following gives the definition of the Legendre symbol.
is quadratic residue modulo p. The following gives the definition of the Legendre symbol.
The Jacobi symbol  has the same look as the Legendre symbol. The top argument can be any integer. The bottom argument is an odd positive integer. If the odd positive integer
has the same look as the Legendre symbol. The top argument can be any integer. The bottom argument is an odd positive integer. If the odd positive integer  has the prime factorization
has the prime factorization  , the Jacobi symbol is defined as follows:
, the Jacobi symbol is defined as follows:
For convenience, we define  . A slightly different, but equivalent, definition is that whenever the odd integer
. A slightly different, but equivalent, definition is that whenever the odd integer 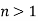 has the prime factorization
has the prime factorization 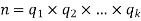 (the prime numbers
(the prime numbers 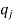 are not necessarily distinct), the symbol
are not necessarily distinct), the symbol 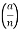 is defined as follows:
is defined as follows:
According to the prime factorization of the bottom argument, the Jacobi symbol is defined using the Legendre symbol.
Q6) State the properties of jacobi Symbol.
A6)
There are two natural questions now that the Jacobi symbol has been defined based on the Legendre symbol.
Does the value of 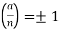 indicates that
indicates that 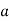 is a quadratic residue or nonresidue modulo
is a quadratic residue or nonresidue modulo  ?
?
The Legendre symbol is a flexible tool because it follows a set of principles (for example, the law of quadratic reciprocity). Is the Jacobi sign compliant with these guidelines? In theory, evaluating the Jacobi symbol entails factoring the sign's bottom argument. This appears to be a limitation at first glance. However, if the Jacobi symbol follows the Legendre symbol's laws, including the law of quadratic reciprocity, evaluating the Jacobi symbol will be equally as simple.
For the first question, the following is true: If 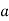 is a quadratic residue modulo
is a quadratic residue modulo 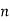 , then
, then 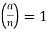 . The contrapositive of this statement is that if
. The contrapositive of this statement is that if  , then the number
, then the number 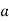 is a quadratic nonresidue modulo the odd integer
is a quadratic nonresidue modulo the odd integer  , i.e. the equation
, i.e. the equation  has no solutions. However, the value of
has no solutions. However, the value of  does not imply that
does not imply that 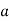 is a quadratic residue modulo
is a quadratic residue modulo  . For example,
. For example,  but the equation
but the equation 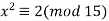 has no solutions. Note that both equations
has no solutions. Note that both equations  and
and 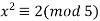 have no solutions. This means that the value of
have no solutions. This means that the value of  is the product of two Legendre symbols of -1.
is the product of two Legendre symbols of -1.
Q7) Explain Legendre symbol
A7)
In number theory, the Legendre symbol is a quadratic character modulo an odd prime number p with values 1, 1, 0: its value at a (nonzero) quadratic residue mod p is 1 and at a non-quadratic residue (non-residue) is 1. At zero, it has no value.
Adrien-Marie Legendre introduced the Legendre symbol in 1798[1] as part of his attempts to prove the law of quadratic reciprocity. The Jacobi symbol and higher-order Dirichlet characters are examples of generalisations of the symbol. The Legendre symbol inspired the invention of several other "symbols" used in algebraic number theory, such as the Hilbert symbol and the Artin symbol, due to its notational convenience.
Q8) State the properties of Legendre Symbol?
A8)
The Legendre symbol has a number of helpful qualities that, when combined with the law of quadratic reciprocity, can be utilised to efficiently compute it.
- The Legendre symbol reveals the parity of a non-zero integer mod p. That is, given a generator
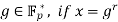 , the n X is a quadratic residue if and only if r is even. This also shows that half of the non-zero elements in
, the n X is a quadratic residue if and only if r is even. This also shows that half of the non-zero elements in 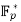 are quadratic residues.
are quadratic residues. - If

 then the fact tha
then the fact tha
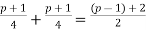 gives us that
gives us that  is the square root of the quadratic residue x.
is the square root of the quadratic residue x.
The Legendre symbol is periodic in its first (or top) argument: if a ≡ b (mod p), then

- The Legendre symbol is a completely multiplicative function of its top argument:
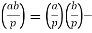
A residue is formed by the product of two numbers that are both quadratic residues or quadratic non-residues modulo p, whereas a non-residue is formed by the product of a residue and a non-residue. The Legendre sign of a square is an exception:

- When viewed as a function of a, the Legendre symbol (a/p) is the unique quadratic (or order 2) Dirichlet character modulo p.
- The first supplement to the law of quadratic reciprocity:
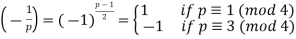
- The second supplement to the law of quadratic reciprocity:

- Special formulas for the Legendre symbol (a/p) for small values of a:
- For an odd prime p ≠ 3,
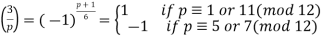
- For an odd prime p ≠ 5,

- The Fibonacci numbers 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, … are defined by the recurrence F1 = F2 = 1, Fn+1 = Fn + Fn−1. If p is a prime number then
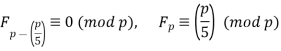
For example,
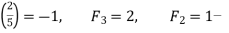




Q9) Explain Quadratic reciprocity.
A9)
The Legendre symbol is considerably aided by the law of quadratic reciprocity, which was discovered by Euler and Legendre and verified by Gauss.
We'll start with the following theorem:
Theorem: Let p be an odd prime and q be some integer coprime to p. Let m=⌊q/p⌋+⌊2q/p⌋+...+⌊((p−1)/2)q/p⌋.
Then m=u+(q−1)(mod2), where as in Gauss' Lemma, u is the number of elements of {q,2q,...,q(p−1)/2} which have a residue greater than p/2. In particular when q is odd, m=u(mod2).
Proof: For each i=1,...,(p−1)/2, the equation iq=p⌊iq/p⌋+ri holds for some 0<ri<p. Reading the proof of Gauss' Lemma, we see these are precisely the bi and ci.
Then summing these equations modulo 2 gives
q(p2−1)/8=pm+b1+...+bt+c1+...+cu=pm+b1+...+bt+up+(p−c1)+...+(p−cu)=pm+up+1+2+...+(p−1)/2=pm+up+(p2−1)/8
Since p is odd, we have m=u+q−1(mod2).
Theorem (Law of Quadratic Reciprocity): Let p,q be distinct odd primes. If p=q=−1(mod4), then
(pq)=−(qp)
Otherwise
(pq)=(qp).
Which we can state as
(pq)(qp)=(−1)p−12q−12
Proof: From above, we need only show
m+n=(p−1)(q−1)/4
Where m=⌊q/p⌋+⌊2q/p⌋+...+⌊((p−1)/2)q/p⌋, and n is similarly defined by swapping p and q.
Eisenstein discovered a beautiful geometrical proof. Consider the line L from (0,0) to (p,q), as well as the rectangle R with (0,0) and (p/2,q/2) corners. How many lattice points are completely included within R?
When you calculate the area of a rectangle, you get (p1)(q1)/4. Alternatively, because no lattice points may lie on L in R because p,q are coprime, we can count the number of points above and below L inside R.
Consider the points on the x=1 line below L. 1,2,...,q/p are their y-coordinates. There are 2q/p points for x=2, and so on, for a total of m points below the L. Similarly, in R, there are n points above L, proving the conclusion.
We can restate the proof algebraically. Consider the numbers py−qx for x=1,...,(p−1)/2 and y=1,...,(q−1)/2. There are a total of (p−1)(q−1)/4 numbers, This is not always the case. Because p and q are coprime, none of them are zero. After noticing that n of them are positive and m are negative, the result follows.
Example:
(31103)=−(10331)=−(1031)=−(231)(531)=−(−1)(531)
Since 2=−5(mod8). Next,
(531)=−(315)=−(15)=−1.
Hence 31 is a quadratic nonresidue modulo 103.
We could assume we should stick to our initial modular exponentiation for computing the Legendre symbol because this method is faulty because it relies on factoring. But it turns out that if we extend the Legendre sign, everything is OK.
Q10) Explain Quadratic congruences
A10)
An integer q is called a quadratic residue modulo n in number theory if it is congruent to a perfect square modulo n; that is, if there exists an integer x such that:
If q is not a quadratic nonresidue modulo n, it is called a quadratic nonresidue modulo n.
Quadratic residues, originally an abstract mathematical term from the branch of number theory known as modular arithmetic, are today used in applications ranging from acoustical engineering to encryption and huge number factoring.
Q11) What is composite moduli?
A11)
If the modulus n has been factored into prime powers the solution was discussed above.
If n is not congruent to 2 modulo 4 and the Kronecker symbol 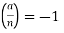 then there is no solution; if n is congruent to 2 modulo 4 and
then there is no solution; if n is congruent to 2 modulo 4 and 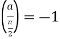 , then there is also no solution. If n is not congruent to 2 modulo 4 and ,
, then there is also no solution. If n is not congruent to 2 modulo 4 and , 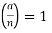 or n is congruent to 2 modulo 4 and
or n is congruent to 2 modulo 4 and 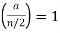 , there may or may not be one.
, there may or may not be one.
If the complete factorization of n is not known, and  and n is not congruent to 2 modulo 4, or n is congruent to 2 modulo 4 and
and n is not congruent to 2 modulo 4, or n is congruent to 2 modulo 4 and 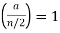 , the problem is known to be equivalent to integer factorization of n (i.e. an efficient solution to either problem could be used to solve the other efficiently).
, the problem is known to be equivalent to integer factorization of n (i.e. an efficient solution to either problem could be used to solve the other efficiently).
The above discussion indicates how knowing the factors of n allows us to find the roots efficiently. Say there were an efficient algorithm for finding square roots modulo a composite number. The article congruence of squares discusses how finding two numbers x and y where x2 ≡ y2 (mod n) and x ≠ ±y suffices to factorize n efficiently. Create a random integer, square it modulo n, and use the square root procedure to get the root. Repeat until it gives a number that is not identical to the one we squared (or its negative modulo n), then use the congruence of squares procedure. The efficiency of the factoring algorithm is determined by the root-exact finder's properties.
Computing the Legendre symbol quickly determines whether an is a quadratic residue or a nonresidue modulo n (denoted a R n or a N n) for prime n. For composite n, however, this results in the quadratic residuosity problem, which is not known to be as difficult as factorization but is thought to be difficult.
However, if we want to know if there is a solution for x less than a specific limit c, this problem is NP-complete; however, it is a fixed-parameter tractable problem, where c is the parameter.
In general, the following theorem can be used to determine if an is a quadratic residue modulo composite n:[37]
Let n > 1, and gcd(a,n) = 1. Then x2 ≡ a (mod n) is solvable if and only if:
- The Legendre symbol
 for all odd prime divisors p of n.
for all odd prime divisors p of n. - a ≡ 1 (mod 4) if n is divisible by 4 but not 8; or a ≡ 1 (mod 8) if n is divisible by 8.
Note: This theorem essentially requires that the factorization of n is known. Also notice that if gcd(a,n) = m, then the congruence can be reduced to a/m ≡ x2/m (mod n/m), but then this takes the problem away from quadratic residues (unless m is a square).
Q12) Explain Quadratic congruence with composite moduli.
A11)
An integer q is called a quadratic residue modulo n in number theory if it is congruent to a perfect square modulo n; that is, if there exists an integer x such that:
If q is not a quadratic nonresidue modulo n, it is called a quadratic nonresidue modulo n.
Quadratic residues, originally an abstract mathematical term from the branch of number theory known as modular arithmetic, are today used in applications ranging from acoustical engineering to encryption and huge number factoring.
Composite moduli
If the modulus n has been factored into prime powers the solution was discussed above.
If n is not congruent to 2 modulo 4 and the Kronecker symbol  then there is no solution; if n is congruent to 2 modulo 4 and
then there is no solution; if n is congruent to 2 modulo 4 and  , then there is also no solution. If n is not congruent to 2 modulo 4 and ,
, then there is also no solution. If n is not congruent to 2 modulo 4 and ,  or n is congruent to 2 modulo 4 and
or n is congruent to 2 modulo 4 and  , there may or may not be one.
, there may or may not be one.
If the complete factorization of n is not known, and  and n is not congruent to 2 modulo 4, or n is congruent to 2 modulo 4 and
and n is not congruent to 2 modulo 4, or n is congruent to 2 modulo 4 and  , the problem is known to be equivalent to integer factorization of n (i.e. an efficient solution to either problem could be used to solve the other efficiently).
, the problem is known to be equivalent to integer factorization of n (i.e. an efficient solution to either problem could be used to solve the other efficiently).
The above discussion indicates how knowing the factors of n allows us to find the roots efficiently. Say there were an efficient algorithm for finding square roots modulo a composite number. The article congruence of squares discusses how finding two numbers x and y where x2 ≡ y2 (mod n) and x ≠ ±y suffices to factorize n efficiently. Create a random integer, square it modulo n, and use the square root procedure to get the root. Repeat until it gives a number that is not identical to the one we squared (or its negative modulo n), then use the congruence of squares procedure. The efficiency of the factoring algorithm is determined by the root-exact finder's properties (e.g., does it return all roots?). Is it only the tiniest one? (Will it be a random one?), but it will be effective. [35]
Computing the Legendre symbol quickly determines whether an is a quadratic residue or a nonresidue modulo n (denoted a R n or a N n) for prime n. For composite n, however, this results in the quadratic residuosity problem, which is not known to be as difficult as factorization but is thought to be difficult.
However, if we want to know if there is a solution for x less than a specific limit c, this problem is NP-complete; however, it is a fixed-parameter tractable problem, where c is the parameter.
In general, the following theorem can be used to determine if an is a quadratic residue modulo composite n:[37]
Let n > 1, and gcd(a,n) = 1. Then x2 ≡ a (mod n) is solvable if and only if:
- The Legendre symbol
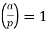 for all odd prime divisors p of n.
for all odd prime divisors p of n. - a ≡ 1 (mod 4) if n is divisible by 4 but not 8; or a ≡ 1 (mod 8) if n is divisible by 8.
Note: This theorem essentially requires that the factorization of n is known. Also notice that if gcd(a , n)= m, then the congruence can be reduced to a/m ≡ x2/m (mod n/m), but then this takes the problem away from quadratic residues (unless m is a square).
Q13) The following table exhibits the orders modulo 13 of the positive integers less than 13:
A12)
Integer | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Order | 1 | 12 | 3 | 6 | 4 | 12 | 12 | 4 | 3 | 6 | 12 | 2 |
The order of 2 modulo 13 is 12, but the orders of 22 and 23 are 6 and 4, respectively; this is simple to prove.
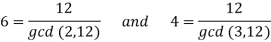
The integers that likewise have order 12 modulo 13 are powers 2k for which gcd(k, 12) = 1 according to Theorem 8.3.

If an integer 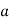 has the largest order possible, then we call it a primitive root of
has the largest order possible, then we call it a primitive root of  .
.
Q14)  .
.
A13)
To determine whether this equation is solvable, we can check each integer in the interval  . Euler's Criterion reduces the solvability question to a modular exponential problem. It can be shown that
. Euler's Criterion reduces the solvability question to a modular exponential problem. It can be shown that  . Thus
. Thus 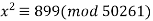 has solutions.
has solutions.
On the other hand, the equation 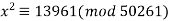 has no solutions since
has no solutions since 
Q15) Using Euler's Criterion for quadratic residues and Legendre symbols, determine if 2, 3, or 5 are primitive roots of 5639.
A14)
We first note that the possible orders of 5369 are divisors of 5368. The divisors of 5368 are 1, 2, 2819, 5638. We note that the orders of 2, 3, 5, and 7 will not be 1 or 2. We can thus check to see if the orders of 2, 3, 5 or 7 are 2819.
Now we know that from Euler's Criterion that  . Given that, we can evaluate the Legendre symbols (2/5369),(3/5369),(5/5369),(7/5369).
. Given that, we can evaluate the Legendre symbols (2/5369),(3/5369),(5/5369),(7/5369).
The Legendre symbol (2/5369)=1 since 5369≡1(mod8). Hence 2 is NOT a primitive root of 5369, since 2 has order 2819.
The Legendre symbol (3/5369)=(5369/3)=(2/3)=−1. Hence 3 IS a primitive root of 5369, since 3 has order 2819.
The Legendre symbol (5/5369)=(5369/5)=(4/5)=1. Hence 5 is NOT a primitive root of 5369, since 5 has order 2819.
Q16) Calculate the Legendre symbol (1000/11).
A15)
We know that 11 is an odd prime, and 11∤1000, so the Legendre symbol (1000/11) is defined. Let's start with a breakdown of 1000's prime power decomposition. That is, 1000=23⋅53. Hence it follows that by (D) that:

By (C), we know that  , and
, and  , hence:
, hence:
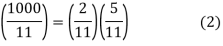
By (I), we know that  since 11≡3(mod8):
since 11≡3(mod8):
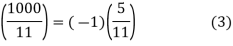
5≡1(mod4), and 11≡3(mod4). By (G), we know that 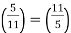 hence:
hence:
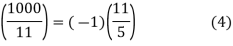
By (B), we can reduce 11. That is 11≡1(mod5), so:

And by (C), 1 is a square, so  Hence
Hence


Hence the Legendre symbol (1000/11)=−1. Hence the quadratic congruence x2≡1000(mod11) has no solutions since 1000 is a quadratic nonresidue (mod 11).
Q17) Does the quadratic congruence x2≡341(mod17) have solutions?
A16)
We can determine if this quadratic congruence has solutions by evaluating the Legendre symbol (341/17). By (A), we know this Legendre symbol is defined since 17 is an odd prime and 17∤341. For evaluating this Legendre symbol, we are going to first use (B) to reduce 341. Note that we could have used this in example 1 too! 341≡1(mod17). Hence it follows that:
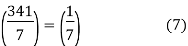
And since 1 is a square, then  Hence it follows that the Legendre symbol (341/17)=1. So the quadratic congruence x2≡341(mod17) has solutions. In fact, we can find them rather easily:
Hence it follows that the Legendre symbol (341/17)=1. So the quadratic congruence x2≡341(mod17) has solutions. In fact, we can find them rather easily:
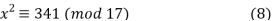
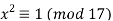
As a result, x is either 1 (mod 17) or -1. (mod 17). Because -1 isn't in least residue, we'll use 16 instead (mod 17). As a result, our answers are x = 1 and x = 16.
Q18) Evaluate the Legendre symbol (14014/5).
A17)
We know that this Legendre symbol is defined since 5 is an odd prime and 5∤14014. Using property (B), we know that 14014≡4(mod5). Hence:
We know that 4 is a square since 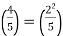 Hence (14014/5)=1.
Hence (14014/5)=1.
Q19) Evaluate the Legendre symbol (342/113).
A18)
Once again, this Legendre symbol is defined. By property (B), 342≡3(mod113). This Legendre symbol is specified once more. 3423, according to property (B) (mod113). Hence:

It's worth noting that 3(mod4) and 3(mod1) (mod4). As a result of (G):

We get 1132(mod3) by lowering 113 (mod 3), so:

Notice that 3≡3(mod8), so by (I), 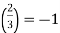 and hence the Legendre symbol (342/113)=−1.
and hence the Legendre symbol (342/113)=−1.
Q20) Let 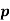 be a prime number. Prove that there exists x∈Z for which p ∣ x2−x+3 if and only if there exists y∈Z for which p ∣ y2−y+25.
be a prime number. Prove that there exists x∈Z for which p ∣ x2−x+3 if and only if there exists y∈Z for which p ∣ y2−y+25.
A19)
The statement is trivial for p≤3, so we can assume that p≥5.
Since p ∣ x2−x+3 is equivalent to p ∣ 4(x2−x+3)=(2x−1)2+11, integer x exists if and only if −11 is a quadratic residue modulo p. Likewise, since 4(y2−y+25)=(2y−1)2+99, y exists if and only if −99 is a quadratic residue modulo p. Now the statement of the problem follows from

Q21) Solve  .
.
A20)
According to Euler’s Criterion, the equation  has solutions since
has solutions since  . To find the solutions, we keep adding the modulus to
. To find the solutions, we keep adding the modulus to  until we get a perfect square.
until we get a perfect square.

So we have  , which gives
, which gives 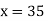 and
and 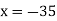 . The solutions are
. The solutions are 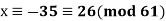 and
and 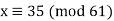 .
.
Q22) Solve 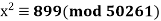 .
.
A21)
Since 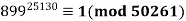 , the equation has solutions. We then add the modulus repeatedly to 899 until we get a perfect square (with the aid of an Excel spreadsheet)
, the equation has solutions. We then add the modulus repeatedly to 899 until we get a perfect square (with the aid of an Excel spreadsheet)
So we have  , which gives
, which gives  and
and 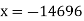 . The solutions are
. The solutions are  and
and  .
.
Q23) Solve 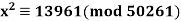
A22)
Since  , the equation has no solutions according to Euler’s Criterion.
, the equation has no solutions according to Euler’s Criterion.