Unit - 1
Introduction to Thermodynamics and Entropy
Q1) For silver, the molar specific heat at constant pressure in the range 50 to 100 K is given by
Cp = 0:076 T -0.00026 T2 — 015 cal/K
Where T is the Kelvin temperature.
Lf 2 mole of silver is heated from 50 to 100 K, calculate
(i) Heat required
(ii) Change in entropy.
A1)
(i) If 2 moles, of silver are raised in temperature by dT, the quantity of heat required
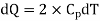
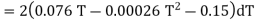
Since the temperature is increased from 50 K to 100 K, hence quantity of heat required for this Purpose



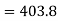 calories
calories
(ii) Change in entropy when silver is heated 50K to 100K
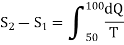



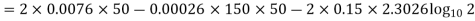
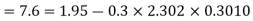
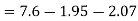
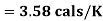
Q2) A Carnot engine is working between 500K and 400K. Calculate efficiency?
A2)
Given 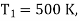
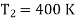
Efficiency of the engine 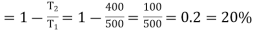
Q3) Two Carnot engines A and B are operated in series. The first one A, receives heat 900 K and rejects to a. Reservoir at temperature TK. The second engine B receives the heat rejected by the first engine and in ban rejects to a heat reservoir at 400 K. Calculate the temperature T for the situation when:
(i) The work outputs of the two engines are equal.
(ii) 11th efficiencies of the two engines are equal.
A3)
The efficiency of a Carnot's engine is given by
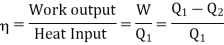
Or, on the Kelvin’s temperature scale,
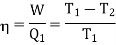
Now for engine A; 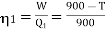
And for engine B, 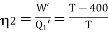
(i) when work outputs of the two engines are equal i.e.,
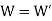
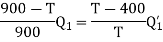
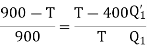
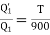 (From property of Carnot’s cycle)
(From property of Carnot’s cycle)

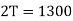
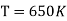
(ii) When efficiencies of two engines are equal.
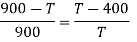
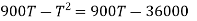
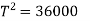

Q4) What is Zeroth law of thermodynamics?
A4)
Let us analyse a situation in which two systems are separated by a diathermic (good conductor of heat) and adiabatic (bad conductor of heat) walls. Now Let us consider the systems A, B, C in which A and B are isolated from each other through an adiabatic wall and both are in contact with C through diathermic wall as is shown in figure. As time passes A and B will separately attain equilibrium with C. Now if the diathermic and adiabatic walls are interchanged, no further change in states of any of the three systems will occur. This indicates that system A and B themselves are in thermal equilibrium before the walls are interchanged.
This experimental observation was first developed by R.H Fowler in 1931 and was named as Zeroth law of thermodynamics which can be stated as follows:
"If two systems are separately in thermal equilibrium with a third one, then they themselves are in thermal equilibrium with each other."
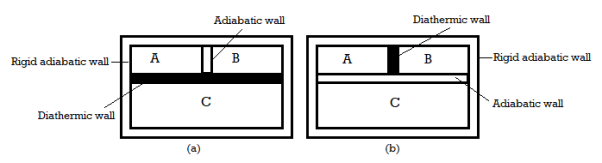
Figure 1: Zeroth law of thermodynamics
"If a system A is in thermal equilibrium with each of the several other systems B, C, D, E etc., separately then any pair among B, C, D, E etc., will be in mutual thermal equilibrium i.e., D and C or B and D or B and C are always in equilibrium." Zeroth law permits us to assert that all systems in thermal equilibrium with each other have a common property. We call this common property as temperature.
The temperature is a property of a system that determines whether or not a system is in thermal equilibrium with other systems.
Equal temperatures imply thermal equilibrium; unequal temperatures imply its absence. Thus, the zeroth law gives the concept of temperature.
Q5) Discuss First law of thermodynamics?
A5)
The first law of thermodynamics is simply the principle of conservation of energy applied to a thermodynamic system. This law can be explained as follows: -If a quantity of heat dQ is supplied to a body, then in general it is used in three ways. (i) Partially, it is used in raising the temperature of the body i.e., increasing its internal kinetic energy dUK.
(ii) Partially, it is used in doing internal work against molecular attraction, i.e., increasing the internal potential energy dUp.
(iii) And rest is used in expanding the body against the external pressure i.e., in doing external work dW.
So, above statement can be written as,
DQ = dUK + dUp + dW ……….. (1)
This is the differential form of the first law of thermodynamics.
But we know
DU = dUK + dUp
So, equation (1) can be written as
DQ = dUK + dW ……….. (2)
Can also be written as
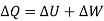 ……….. (3)
……….. (3)
We should note that, Equation (2) represents the differential form whereas eq. (3) stands for change in respective quantities.
 Q,
Q, 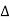 U and
U and  W are to be measured in the same unit i.e., all the three either in joules or in calories.
W are to be measured in the same unit i.e., all the three either in joules or in calories. - If the heat is taken by the body, then
 Q is positive and if it is given by the body
Q is positive and if it is given by the body  Q is negative.
Q is negative. - Similarly, if the work is done by the system, then
 W is positive and if the work is done on the system, then
W is positive and if the work is done on the system, then  W is negative.
W is negative.
Q6) Discuss Important features of First law of thermodynamics and its Limitations?
A6)
Important features of first law of thermodynamics
- Heat is a form of energy.
- Energy is conserved in a thermodynamic system process.
- Every thermodynamic system in equilibrium state possesses internal energy and this internal energy is a function of its state i.e., temperature only.
- It is applicable to any process by which a system undergoes a physical or chemical change.
Limitations of the first law of thermodynamics are discussed below
No restriction on the direction of the flow of the heat: the first law establishes definite relationship between the heat absorbed and the work performed by a system. However, it does not indicate whether heat can flow from a cold end to a hot end or not. For example: we cannot extract heat from the ice by cooling it to a low temperature. Some external work needs to be done.
Does not specify the feasibility of the reaction: first law does not specify that process is feasible or not. For example, when a rod is heated at one end then equilibrium has to be obtained which is possible only by some expenditure of energy.
Practically it is not possible to convert the entire heat energy into an equivalent amount of work. To overcome these limitations, another law is needed which is known as second law of thermodynamics.
Q7) What do you mean by reversible and irreversible process?
A7)
Reversible Process
A reversible process is one which can be reversed in such a way that all changes taking place in the direct process are exactly repeated in the inverse order and opposite sense, and no changes are left in any of the bodies taking part in the process or in the surroundings.
For example, if an amount of heat is supplied to a system and an amount of work is obtained from it in the direct process; the same amount of heat should be obtainable by doing the same amount of work on the system in the reverse process.
Conditions of Reversibility A process can be reversible only when it satisfies two conditions:
(i) Dissipative forces such as friction, viscosity, inelasticity, electrical resistance, magnetic hysteresis etc. must be completely absent.
Suppose a gas is contained in a cylinder fitted with a piston and placed in contact with a constant-temperature source. The piston is loaded so that the pressure exerted by the piston on the gas exactly balances the pressure of the gas on the piston. If the load on the piston is now decreased, the gas will expand, doing external work in pushing up the piston and also in overcoming the friction between the piston and the walls of the cylinder. The heat necessary for this work is taken from the source. If now the load on the piston is increased, the gas will be compressed. The work used in pushing up the piston during the expansion is now recovered. On the contrary, more work has to be done against the friction. The expansion is therefore irreversible. Similarly, other dissipative effects like inelasticity, electrical resistance, etc. make the process irreversible.
(ii) The process must be quasi-static.
When the gas expands, an amount of work is done by the gas to give kinetic energy to the piston. This work cannot be recovered during the reverse process, but on the contrary, more work is to be done to give kinetic energy to the piston. Hence in order to make the expansion of the gas reversible, the pressure of the gas on the piston should be only infinitesimally different from the pressure exerted by the piston on the gas. Under the condition the expansion or compression will take place infinitely slowly so that no kinetic energy will be produced. These conditions are never realized in practice. Hence a reversible process is only an ideal conception.
Irreversible Processes
Any process which is not exactly reversible is an irreversible process. All practical processes such as free expansion, Joule-Thomson expansion, electrical heating of a wire, diffusion of liquids and gases etc., are irreversible processes. All natural processes such as conduction, radiation, radioactive decay etc., are also examples of irreversible process.
Q8) What is second law of thermodynamics?
A8)
The second law of thermodynamics helps us to predict whether the reaction is feasible or not and determines direction of the flow of heat. The second law also tells that certain amount of heat energy cannot be completely converted into equivalent amount of work.
The first law of thermodynamics states the equivalence of mechanical work and heat. When one is completely converted into other (W=Q). Thus, it is the principle of conservation of energy applied to a thermodynamic system.
However, we propose to extract a certain quantity of heat from a body and convert it completely into work. The first law would not be violated. But. In actual practice this is found to be impossible. If this were possible, we could drive ships across an ocean by extracting heat from the water of the ocean. Thus, the first law simply tells that if a process takes place, energy will remain conserved. It does not tell us whether the process is possible or not. Similarly, of a hot body and a cold body are brought in contact the first law is not violated whether the heat flows from the hot to the cold body or vice-versa. By experience we know that heat never flows from cold to hot body. The purpose of the second law is to incorporate such experimental facts into thermodynamics.
There are statements of the second law of thermodynamics proposed by different scientists-(i) Kelvin-Planck statement (ii) Clausius statement
Kelvin-Planck's Statement
In a heat engine, a working substance takes in heat from a hot body converts a part of it into mechanical work, and gives out the rest to a cold body. No engine has ever been designed which can operate in a cycle by taking heat from a body and converting all of it into work; some heat must always be given to a colder body. This experience led Kelvin and Planck to state the following:
It is impossible to construct a device which operating in a cycle, will take heat from a body and convert it completely into work, without leaving any change anywhere.
Clausius Statement
In a refrigerator, a working substance takes in heat from a cold body, has a net amount of work done on it by an external agent (electric supply), and gives out a larger amount of heat to a hot body. It thus transfers heat from a cold body to a hot body with the aid of external work or energy. No refrigerator has ever been designed which can run without supply of external energy. This experience led Clausius to state that:
"It is impossible to construct a device which operating in a cycle, will take heat from a cold body and reject it to a hot body without expenditure of work by an external energy source". In other words-heat cannot flow spontaneously from a colder body to a hotter body.
Q9) Give equivalence of Kelvin-Planck and Clausius statements?
A9)
We can show that these two statements of the second law are equivalent
Let us suppose that there is a refrigerator R (Figure 2) which transfers an amount of heat Q2 from a cold body to a hot body without having any supply of external energy. It is this against the Clausius statement.
Now, suppose an engine E working between the same hot and cold bodies takes in heat Q1 from the hot body, converts a part (W = Q1-Q2) into work, and gives up the remaining heat Q2 to the cold body.
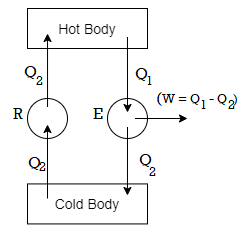
Figure 2: Thermodynamic System
The engine E alone does not violate the law. But if the refrigerator R and the engine E are combined together, they form a device that takes in heat Q1-Q2 from the hot body and converts all into work without giving up any amount to the cold body. This is clearly against the Kelvin-Planck statement.
Similarly, let us suppose that there is an engine E (Figure 3) which takes in an amount of heat Q1 from a hot body and converts it completely into work W(=Q1), without giving any heat to the cold body. It is against the Kelvin-Planck statement.
Now, suppose a refrigerator R working between the same hot and cold bodies takes in heat Q2 from the cold body, has work W(=Q1) done upon it by an external agent, and gives out heat Q1+Q2 to the hot body. The refrigerator R alone does not violate the law. But both E and R together form a device which transfers an amount of heat Q2 from a cold body to a hot body with no external energy source. This is clearly against the Clausius statement.
The second law of thermodynamics supplements the first law. The first law simply tells us that any device cannot deliver more energy than it receives. It does not speak regarding any limitation, or any condition necessary for the delivery of energy.
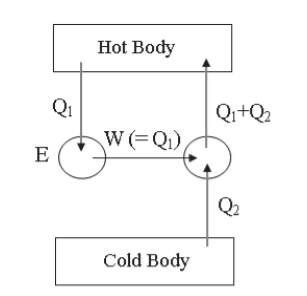
Figure 3: Thermodynamic System
The second law, however, does it. For example, heat taken in by a substance cannot be all delivered as work, or heat cannot flow spontaneously from a colder to a hotter body. These phenomena are not disallowed by the first law, but they are disallowed by the second law.
Q10) What is Carnot’s Theorem?
A10)
The second law of thermodynamics gives two important conclusions which can be taken together in the form of a theorem called Carnot's theorem. According to this theorem "The efficiency of a Carrot reversible engine is maximum and is independent of the nature of the working substance".
Or
"The efficiency of all reversible heat engines operating between the same two temperatures is the same and no irreversible heat engine working between the same two temperatures can have greater efficiency than Carnot's reversible heat engine".
To prove it, let us consider two heat engines EA and ER operating between a source at temperature T1 and sink at temperature T2 (Figure). Let EA be any heat engine and ER be a reversible heat engine. Let us assume efficiency ηA of EA is greater than efficiency ηR of ER.
In order to prove the Carrot theorem, we have to contradict our assumption.
Let the rates of working of the engine EA be Q1A and that of ER be Q1R such that-
Q1A=Q1R=Q1
As Assumed
ηA > ηR
As we know that
So, we can write
Therefore

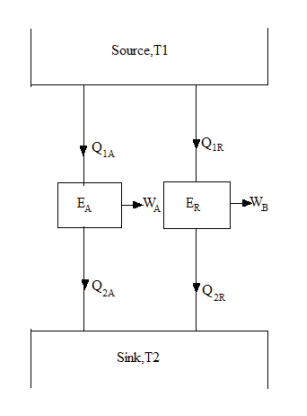
Figure 4: Carnot’s Theorem
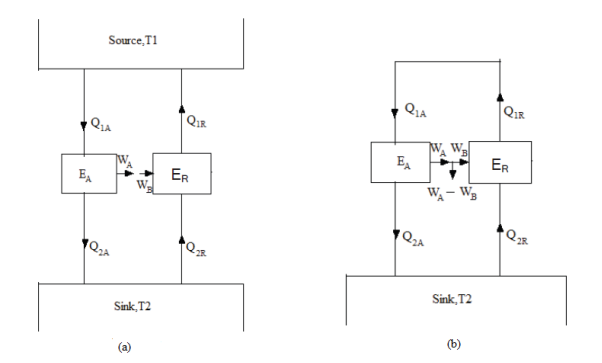
Figure 5: Carnot’s Theorem
Let us reverse ER. Since ER is a reversible heat engine, therefore, the magnitude of heat transferred and work done will remain the same but their directions will reverse (Figure).
Since WA > WR some part of WA which is equal to WR in magnitude can be fed to drive the reversed heat engine ER. Since, Q1A =Q1R = Q1, the heat discharged by ER may be supplied to EA thus the source may be eliminated. The net result is that EA and ER together constitute a heat engine which operating in a cycle produces a net work done WA-WR (Figure). While exchanging heat with a single reservoir at temperature T2, thus violating the Kelvin-Planck statement. Hence our assumption is wrong.
Therefore, ηA < ηR and this proves the Carrot theorem.
Carnot engine as a refrigerator
When a Carnot engine works in the reverse direction i.e., when it absorbs Q2 amount of heat from the sink and work W is done on the working substance and finally Q1 amount of heat is rejected to the source at higher temperature, the arrangement acts like a refrigerator. The efficiency of a refrigerator is measured in terms of coefficient of performance.
The coefficient of performance k is defined as the ratio of the heat absorbed from the sink to the work done on the working substance by the external agent.
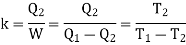
Hence the value of k is greater than unity.
Q11) Discuss Thermodynamic scale of temperature and its equivalence to perfect gas scale?
A11)
According to the law, heat always flows from a body at a higher temperature to a body at the lower temperature. This law is applicable to all types of heat engine cycles including Otto, Diesel, etc. for all types of working fluids used in the engines. This law has led to the progress of present-day vehicles.
Another application of this law is refrigerators and heat pumps based on the Reversed Carnot Cycle. If you want to move heat from a body at a lower temperature to a body at a higher temperature, then you have to supply external work. In the original Carnot Cycle, heat produces work while in the Reversed Carnot Cycle work is provided to transfer heat from lower temperature reservoir to a higher temperature reservoir.
Removing heat from the food items in the refrigerator and throwing it away to the higher temperature atmosphere doesn’t happen automatically. We need to supply external work via the compressor to make this happen in the refrigerator.
Air conditioner and heat pump follow the similar law of thermodynamics. The air conditioner removes heat from the room and maintains it at a lower temperature by throwing the absorbed heat into the atmosphere. The heat pump absorbs heat from the atmosphere and supplies it to the room which is cooler in winters.
In both the cases above, external work/energy in the form of electricity has to be supplied; larger the temperature difference, larger is the external work required.
Thermodynamic scale of temperature and its equivalence to perfect gas scale
Suppose that the interval between the freezing and the boiling points of water is divided into 100 equal parts on thermodynamic temperature scale.
Tsteam = Tice + 100
Thus, we have
 ……… (1)
……… (1)
The thermodynamic scale is thus completely defined and fixed. Now we will see its identity with the perfect gas.
For a Carnot engine using a perfect gas as the working substance, we know
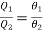 ……… (2)
……… (2)
(Here θ's are used instead of T's, because T's are already in use for absolute scale)
Where θ1 and θ2 are the temperature measured on the perfect gas scale. We have
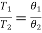 ……… (3)
……… (3)
i.e., the ratios of any two temperatures on the thermodynamic scale and the perfect gas scale are equal. Thus, the absolute zero of the thermodynamic scale coincides with the zero of the perfect gas thermometer, for if T2 = 0, θ2= 0.
Further from eq. (1) and (3) since the interval between the ice point and steam point is 100 on both scales,
Tsteam − Tice = 100
And θ steam − θ ice = 100
Hence, on the efficiency of Carnot engine on perfect gas scale is
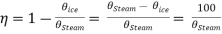 ……… (4)
……… (4)
And on absolute scale is
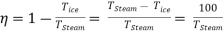 ……… (5)
……… (5)
Since the efficiencies are the same
 ……… (6)
……… (6)
Thus
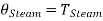 ……… (7)
……… (7)
i.e., the absolute temperature of the boiling point of water is the same, whether measured on the perfect gas scale or on the thermodynamic scale of temperature. In a similar manner it can be shown that any other temperature will have the same value on the two scales, i.e.,
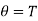 ……… (8)
……… (8)
Thus, the thermodynamic temperature is, therefore, numerically equal to the perfect gas temperature and, in the proper range, may be measured with a gas thermometer.
Q12) Discuss concept of entropy?
A12)
Initially the thermodynamic state of a system was represented by only three variables named pressure, volume and temperature. In 1854, Rudolf Clausius while studying the thermodynamic systems realized that to represent the thermodynamic state of a system, in addition to these three variables there was one quantity named as "Entropy". It was proved successfully that like pressure, volume and temperature the entropy is also a function of the state of the system.
The concept of entropy was introduced for many reasons. The changes in the state of a system can be represented in different ways e.g., the isothermal change (in which the temperature remains unchanged), the isobaric change (in which the pressure remains constant) and the isochoric change (in which the volume of the system remains constant). Now the real question arises that which quantity remains constant during an adiabatic change. It was established that the entropy remains constant in an adiabatic change in the system. The systems have a tendency to change from a more ordered state to a more disordered state. The perception of entropy expresses this in a better physical and mathematical form. The entropy of a substance is a real quantity, just like pressure, volume and temperature. Despite being a very important quantity, it can't be represented in some physical form. It, therefore, becomes very difficult to visualize it and to understand its exact nature. Entropy can be conveniently understood by studying its effect, properties and other aspects.
Let us consider a number of isothermals I1, I2, I3,.... At temperatures T1, T2, T3... Respectively as represented in the P-V diagram. Let Al and A2 are two adiabatic curves which cut the isothermal at points (a, b), (c, d), (e, f) respectively. Consider abcda a Carnot cycle. It works between two temperature T1and T2. Q1 is the amount of heat extracting from source and Q2 is the amount of heat rejecting to sink. Thus, efficiency is given by
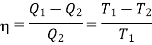
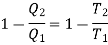
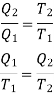
Also, for cdfe, Q2 is the amount of heat extracting from source at T2 and Q3 is the amount of heat rejecting to sink. We have
 …….. (2)
…….. (2)
Similarly, we can obtain for mini Carnot cycles bound by adiabatic Al and A2. Hence
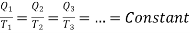 …….. (3)
…….. (3)
And we can write this in general form as
 …….. (4)
…….. (4)
This constant ratio is entropy of the system.
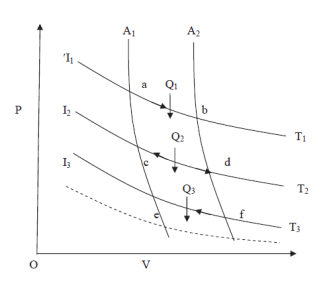
Figure 6: PV diagram
If S1 and S2 are the entropies corresponding to the adiabatic curves Al and A2 respectively, then we can write
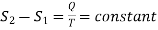 …….. (5)
…….. (5)
If the adiabatic lie very close to each other and dQ is the quantity of heat absorbed or rejected at a temperature T in going from one adiabatic to the other, then change in entropy can be written as
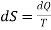 …….. (6)
…….. (6)
In the above discussion, the changes from adiabatic A1 to A2 were considered isothermal but this is not necessary. The only necessary condition is that the change should be reversible.
In general. The change in entropy in passing from one adiabatic to another can be expressed as
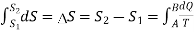 …….. (7)
…….. (7)
The expression
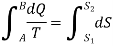
Is a function of the thermodynamic coordinates of a system and refers to the value of the function at the final state minus the value at the initial state. This function is represented by the symbol S and is called entropy.
Since in an adiabatic change, no heat energy is given to or removed from the system i.e., there is no exchange of heat. DQ = 0. Therefore, the change in entropy is zero as given below
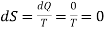 …….. (8)
…….. (8)
In other words, in the adiabatic process, the entropy of a system remains constant. Due to this reason the adiabatic curves on the P-V diagram are called isentropics or constant entropy curves also.
It is, however, difficult to form physical conception of entropy as there is nothing physical to represent it and it cannot be felt like temperature or pressure. Now since
Change in entropy  …….. (9)
…….. (9)
We conclude that dimensions of entropy are the same as the ratio of heat (or energy) and temperature. Its unit is joule/Kelvin (J/K).
Q13) What is Physical significance of entropy?
A13)
The change in the entropy of a substance defined by the relation dS=dq/dt shows that the heat energy has the same dimensions as the product of entropy and absolute temperature. In earth's gravitational field the potential energy of a body is proportional to the product of its mass and the height above some zero level. A comparison indicates that if we regard height as corresponding to temperature, and then mass corresponds to entropy. Thus, entropy of a system is a quantity which bears to heat motion a similar relation as mass bears to linear motion.
Q14) What do you mean by Clausius Theorem and Clausius inequality?
A14)
Clausius Theorem
Let us consider a complete reversible process- a Carrots cycle ABCD as shown in figure. In the isothermal expansion from A to B. The working substance absorbs an amount of heat Q1 at a constant temperature T1 of the source. When the heat is absorbed by the system Q1 is positive and hence entropy change is positive because T1 is positive.
Hence gain in entropy of working substance from A to B = Q1/T1
Source loses this heat Q1 at temperature T1 therefore its entropy decreases by Q1/T1.
During the adiabatic expansion from B to C. There is no change in entropy (since heat is neither taken in nor given out). During the isothermal compression from C to D. The working substance gives out a quantity of heat Q2 to the sink at a constant temperature T2 and therefore the loss in its entropy from C to D = Q2/T2 Q2 (The sink gains this heat Q2 at temperature T2, therefore its entropy increases by Q2/T2.
Again, during the adiabatic compression from D to B, there is no change in entropy.
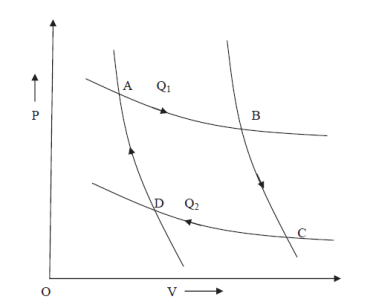
Figure 7: P-V Curve
Thus, the net gain in the entropy of working substance in the whole cycle ABCDA = 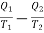
But since in a complete reversible Carrot's cycle
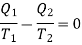
Therefore,
It means that the total change in entropy of the working substance in a complete cycle of reversible process is zero. Similarly, the change in entropy of the combined system of source and sink is also zero. Thus, in a cycle of reversible process, the entropy of the system remains constant or the change in entropy of the system is zero.
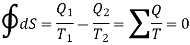
Where the integral sign with a circle refers to a complete cycle. Hence, we conclude that in a reversible cyclic process, the entropy change is zero. This is Clausius theorem.
Clausius inequality
Clausius inequality is given as

The equal sign in the Clausius inequality above applies only to the ideal or Carnot cycle. Since the integral represents the net change in entropy in one complete cycle, it attributes a zero entropy change to the most efficient engine cycle, and makes it clear that entropy does not decrease even in an ideal engine cycle.
The Clausius Inequality applies to any real engine cycle and implies a negative change in entropy on the cycle. That is, the entropy given to the environment during the cycle is larger than the entropy transferred to the engine by heat from the hot reservoir. In the simplified heat engine where the heat Q is all added at temperature T, then an amount of entropy ΔS = Q/T is added to the system and must be removed to the environment to complete the cycle. In general, the engine temperature will be less than T for at least part of the time when heat is being added, and any temperature difference implies an irreversible process. Excess entropy is created in any irreversible process, and therefore more heat must be dumped to the cold reservoir to get rid of this entropy. This leaves less energy to do work.
Q15) Discuss second law of thermodynamics in terms of entropy?
A15)
The second law of thermodynamics is one of the most fundamental laws of nature, having profound implications. The second law - The level of disorder in the universe is steadily increasing. Systems tend to move from ordered behaviour to more random behaviour.
One implication of the second law is that heat flows spontaneously from a hotter region to a cooler region, but will not flow spontaneously the other way. This applies to anything that flows: it will naturally flow downhill rather than uphill.
If you watched a film forward and backwards, you would almost certainly be able to tell which way was which because of the way things happen. A pendulum will gradually lose energy and come to a stop, but it doesn't pick up energy spontaneously; an ice cube melts to form a puddle, but a puddle never spontaneously transforms itself into an ice cube; a glass falling off a table might shatter when it hits the ground, but the pieces will never spontaneously jump back together to form the glass again. Many processes are irreversible, and any irreversible process increases the level of disorder. One of the most important implications of the second law is that it indicates which way time goes - time naturally flows in a way that increases disorder.
The first law of thermodynamics implies, according to Clausius, that the energy of the universe remains constant. The law of conservation of energy. The second law was summed up by him by saying that the entropy of the universe tends to a maximum (law of increase of entropy). We may, therefore, attempt, to write the general statement of second law in terms of-entropy in the following words,
“Every physical or chemical process in nature takes place in such a way so as to increase the entropy of the system.”
In order to formulate the second law mathematically, let SA and SB be the entropies of a substance in initial and final states A and B measured from some & arbitrary zero. The entropy change is then given by

If two two states are infinitesimely close then, above equation become
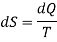
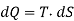
Q16) Calculate the value of entropy for perfect gas?
A16)
Let us calculate the entropy of a perfect gas. Let us consider 1 gram of a perfect gas occupying a volume V at a pressure P and temperature T. Let a quantity of heat dQ be given to the gas, then by the first law of thermodynamics, we have
DQ = dU + dW ……… (1)
If Cv, is the specific heat of the gas at constant volume, dT the rise in temperature, dV the change in volume then we can write
DU= CvdT ……… (2)
And
DW = PdV ……… (3)
Using these values in equation (1) we get
DQ = CvdT + PdV
If S is the entropy per unit mass of the gas, then
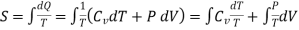 ……… (4)
……… (4)
Now let us calculate the value of S in terms of temperature and volume.
We know,
PV = rT or P/T = r/V, where r is the ordinary gas constant for unit mass of the gas. From equation (4), we get
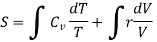

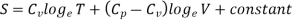 ……… (5)
……… (5)
Where r = Cv - Cp. This is Mayer’s relation. Where Cp is specific heat at constant pressure P.
So, S in terms of P and V can be calculated as given below
PV = rT ……… (6)
Differentiating above equation leads to
PdV +VdP =rdT
PdV = VdP – rdT ……… (7)
From equation (4) we have
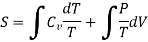

 (since
(since 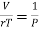 )
)
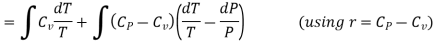
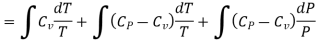
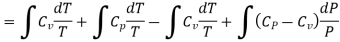
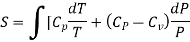
 ……… (8)
……… (8)
We know that
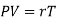 or
or  ……… (9)
……… (9)
Differentiating we get
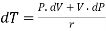 ……… (10)
……… (10)
Putting the value of T in (4)
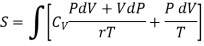
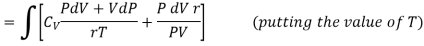
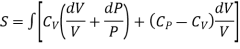
 ……… (10)
……… (10)
In the above calculations, we have assumed the entropy of the gas to be zero at zero temperature. In actual practice, however, we are concerned with a change in entropy of the gas, when the gas changes from a state of pressure P1, volume V1 and temperature T1to another of P2, V2 and T2 respectively. This can be obtained by integrating relation (4) between the limits T1 and T2. If we denote the change in entropy by (S2-S1), then equation (5), (8) and (10) assumes the form, respectively, as
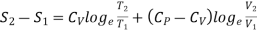 ……… (11)
……… (11)
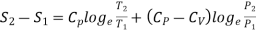 ……… (12)
……… (12)
 ……… (13)
……… (13)
The above relations from stand for unit mass of the gas.
Q17) What is principle of increase of entropy?
A17)
In a reversible process, the entropy remains unchanged while in an irreversible process, it increases. Since, in general, most of the processes are not perfectly reversible, therefore, there is always an increase in the entropy always. If the processes occur in succession the entropy goes on increasing and tends to a maximum value. This is known as the principle of increase of entropy. It may be stated that the entropy of an isolated or self-contained system either increases or remains constant accordingly as the processes it undergoes are irreversible or reversible.
According to Clausius, the entropy of an isolated or self-contained system tends to a maximum value. Thus, the entropy of a system either increases or remains constant i.e.
DS > 0
Where, = sign stands for reversible processes and > sign for irreversible processes. Obviously, for the stability of a system its entropy must be maximum.
Now, since all physical operations in the universe are irreversible, for every such operation performed, a certain quantity of energy of the universe becomes unavailable for useful work and is added to the universe in the form of heat through friction, conduction or radiation. In this way, in a distant future, on account of irreversibility, all energies existing in different forms will be transformed into heat energy and will not be available for alteration into mechanical work, i.e., the available energy of the universe will tend towards zero.
It will correspond to a state of maximum entropy and all temperature difference between various bodies of the universe will be equalized due to convection etc. No heat engine will then be able to work in this state because no heat flow would be possible due to the uniformity of temperature throughout the universe. This is known as the principle of degradation of energy and implies that although the total amount of energy is conserved, it is converted into a form which is unavailable for work.
With an increase in entropy, the thermal agitation and hence disorder of the molecules of substance increases i.e., growth of entropy implies a transition from order to disorder. Thus, the principle of increase of entropy is intimately connected with the less ordered state of affairs.
As the temperature of a system is a measure of its degree of hotness, in a similar way, the entropy of a system is a measure of disorder in it. At absolute zero of temperature, the motion of the molecules of a substance cease, the molecules become well - arranged and the entropy becomes zero.
Q18) How do Entropy changes in reversible processes?
A18)
Let us consider a complete reversible process- a Carrots cycle ABCD as shown in figure. In the isothermal expansion from A to B. The working substance absorbs an amount of heat Q1 at a constant temperature T1 of the source. When the heat is absorbed by the system Q1 is positive and hence entropy change is positive because T1 is positive.
Hence gain in entropy of working substance from A to B = Q1/T1
Source loses this heat Q1 at temperature T1 therefore its entropy decreases by Q1/T1.
During the adiabatic expansion from B to C. There is no change in entropy (since heat is neither taken in nor given out). During the isothermal compression from C to D. The working substance gives out a quantity of heat Q2 to the sink at a constant temperature T2 and therefore the loss in its entropy from C to D = Q2/T2 Q2 (The sink gains this heat Q2 at temperature T2, therefore its entropy increases by Q2/T2.
Again, during the adiabatic compression from D to B, there is no change in entropy.
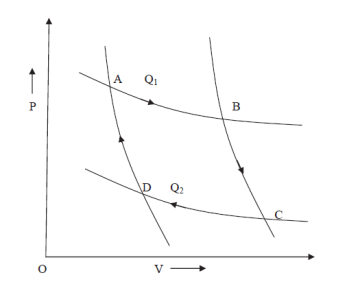
Figure 8: PV Curve
Thus, the net gain in the entropy of working substance in the whole cycle ABCDA = 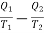
But since in a complete reversible Carrot's cycle
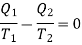
Therefore,
It means that the total change in entropy of the working substance in a complete cycle of reversible process is zero. Similarly, the change in entropy of the combined system of source and sink is also zero. Thus, in a cycle of reversible process, the entropy of the system remains constant or the change in entropy of the system is zero.
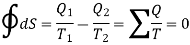
Where the integral sign with a circle refers to a complete cycle. Hence, we conclude that in a reversible cyclic process, the entropy change is zero. This is Clausius theorem.
Q19) How do Entropy changes in irreversible processes?
A19)
Entropy changes in irreversible process
Let us suppose that the working substance in an engine performs an irreversible cycle of changes, absorbing an amount of heat Q1 at a temperature T1 from the source and rejecting the quantity of heat Q2 at a temperature T2 of the sink. Then the efficiency of this cycle is given by
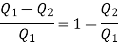
According to Carnot cycle the efficiency is less than that of a reversible engine working between the same two temperature T1 and T2 for which
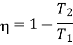


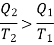
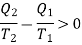
Consider the whole system, system losses the entropy by an amount Q1/T1 and gain by amount Q2/T2. Thus, net change is
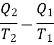
Which is clearly greater than zero or positive. Thus, there is an increase in entropy of the system during an irreversible process. As an example of irreversible process, consider the case of conduction or radiation. Suppose in a system, there are two objects A and B at temperatures T1 and T2 (T1 > T2) respectively. In conduction (or radiation) heat flows from the object of higher temperature to that of lower temperature.
If an amount Q of heat is transferred then
Decrease in the entropy of object A = Q/T1
Increase in the entropy of object B = Q/T2
Therefore, the net increase in entropy
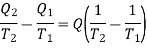
Since T1 > T2, therefore the net increase in entropy is positive. Now we may generalize the result and say that the entropy of a. System increases in all irreversible processes. This is known as the 'Principle of increase of entropy. In the process of equalization of temperature, entropy always increases.
Q20) How can you express Carnot cycle in term of T-S diagram?
A20)
The thermodynamic state of a substance can be determined by plotting the temperature as ordinate and entropy as abscissa. The resulting graph is known as temperature-entropy diagram and is used in the checking of efficient working of actual engines. The idea of T-S graph was first introduced by Gibbs.
If a thermodynamical system is given an infinitesimal amount of heat dQ, at temperature T then
DQ = T dS
Where dS is the increase in the entropy of the system. Therefore, in a process, total amount of heat given to the system is


Figure 9: T-S graph
Obviously, the integral represents the area enclosed by the T-S diagram. Thus by finding the area of T-S diagram, we can find the amount of heat given to the system. The shape of the T-S graph depends upon the process.
An isothermal change is represented by a horizontal line parallel to the entropy axis while an adiabatic change is represented by a vertical line parallel to T-axis because in such a change S remains constant.
Let us study Camot cycle represented by a temperature-entropy (T-S) diagram in figure.

Figure 10: Camot cycle represented by (T-S) diagram
As we know that Carrot's cycle consists of two isothermals and two adiabatics. The isothermals are represented by horizontal straight lines (parallel to entropy axis) and adiabatics by vertical straight lines (parallel to temperature axis) on a T-S diagram.
In this way, in the figure, PQ represents the isothermal expansion at a constant temperature T1 of the source, the vertical line QR is the adiabatic expansion during which there is no change in entropy but a fall of temperature from T1 to T2, the temperature of the sink.
RS is the second isothermal representing compression at constant temperature T2 and SP is the final adiabatic compression involving a rise of temperature from T2 to Tl, entropy remaining the same.
The amount of heat energy absorbed in isothermal expansion PQ is given by the area under PQ, i.e. PQNM.
In a similar way, the heat rejected in isothermal compression RS is given by the area SRNM.
Total heat absorbed = Area PQNM = Tl (S2 – S1)
Heat energy converted into work
= heat absorbed — heat rejected
= area PQNM — area SRNM
= shaded area PQRS
= PS x SR = (T1 — T2) (S2 – S1)
Therefore, efficiency of the engine
η = 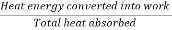

Thus. The T-S diagram gives an expression for efficiency of a Carrot's engine which only depends on the two working temperatures and not on the nature of the working substance.
Q21) What is third law of thermodynamics?
A21)
For the study of chemical equilibrium in chemical reactions. It is necessary to determine the change in the entropy of the system when the reaction takes place at 0 K temperature.
Nernst assumed that this change in entropy is zero. Nernst' s this assumption is termed as Nernst Heat Theorem. Nernst and Simon presented this concept in the form of law which is given as-
'The entropy change associated with any isothermal reversible process of condensed system (solid or liquid) approaches zero as the temperature is reduced to absolute zero."
This is called Third law of thermodynamics.
An important consequence of this law is that it is impossible to attain the absolute zero temperature; it can be attained only asymptotically. Some scientists treated it as a more fundamental law and stated the third law of thermodynamics as follows It is impossible by any process, no matter how idealized, to reduce any system to absolute zero of temperature in a finite number of steps."
The third law of thermodynamics is also known as the law of unattainability of absolute zero of temperature. This law has many applications in physics and chemistry.
Q22) What do you mean by unattainability of absolute zero?
A22)
Unattainability of Absolute Zero
Absolute Zero Temperature
We know
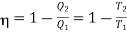 ………. (1)
………. (1)
If T2 =0, then efficiency
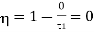
Thus, for the efficiency to be unit i.e.
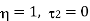
This temperature of the sink at which the efficiency of the reversible engine becomes unity is called the absolute zero of temperature. This is the thermodynamic definition of absolute zero temperature.
From equation (1), it is clear that at the absolute zero of temperature (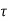 2 =0), Q2 = 0, therefore, W = Q1. Therefore, the entire amount of heat absorbed by the reversible engine is converted into work and thus, the efficiency of the engine becomes unity. The temperature on this scale can never be negative i.e.,
2 =0), Q2 = 0, therefore, W = Q1. Therefore, the entire amount of heat absorbed by the reversible engine is converted into work and thus, the efficiency of the engine becomes unity. The temperature on this scale can never be negative i.e., 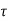 < 0 is not possible. This is because if the temperature of the sink is a negative quantity (say —m) on this scale, then from equation (1)
< 0 is not possible. This is because if the temperature of the sink is a negative quantity (say —m) on this scale, then from equation (1)
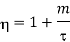
The efficiency will be more than unity (η >1) which is impossible. Because in this situation, the engine will be producing more work than the amount of heat received. This can never be true as it will be a violation of the second law of thermodynamics. Thus, negative temperatures are not possible on the absolute scale of temperature. That is why 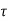 = 0 is the lowest possible temperature and is called the absolute zero temperature.
= 0 is the lowest possible temperature and is called the absolute zero temperature.
It can be easily understood why the efficiency of an engine cannot be unity i.e., 100%. For this to happen we must have a sink at absolute zero temperature. But nature does not provide us with a sink at absolute zero. This temperature is neither available nor easily attainable. Therefore, 100% efficiency of an engine is not possible and thus absolute zero is also unattainable.
Q23) A Carnot engine whose low temperature reservoir is at 70C has efficiency 50%. It is desired to increase the efficiency to 70%. By how many degrees should-the temperature of the high temperature reservoir be increased?
A23)
For this we shall first calculate the temperature of high temperature reservoir

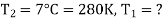
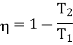
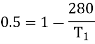
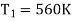

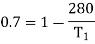
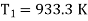
Hence required increase in temperature of high temperature reservoir
= 933.3 — 560 = 373.3 K.