Unit - 2
Classical Statistics - II
Q1) Explain the term Internal Energy.
A1)
Using the ideal gas law, the total molecular kinetic energy contained in an amount M = ρV of the gas becomes,
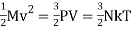 (1)
(1)
The factor 3 stems from the three independent translational degrees of freedom available to point like particles. The above formula thus expresses that there is an internal kinetic energy ½ kT associated with each translational degree of freedom. Whereas monatomic gases like Argon have spherical molecules and thus only the three translational degrees of freedom, diatomic gases like nitrogen and oxygen have stick-like molecules with two extra rotational degrees of freedom orthogonally to the bridge connecting the atoms, and multi-atomic gases like carbon dioxide and methane have the three extra rotational degrees of freedom. According to the equipartition theorem of statistical mechanics these degrees of freedom will also carry a kinetic energy ½ kT per particle. Molecules also possess vibrational degrees of freedom that may become excited, but we shall disregard them here. The internal energy of N particles of an ideal gas is defined to be,
βU =NkT,(2)
Where β is the number of degrees of freedom. Physically a gas may dissociate or even ionize when heated, and thereby change its value of β, but we shall for simplicity assume that β is in fact constant with β = 3 for monatomic, β = 5 for diatomic, and β = 6 for multiatomic gases. For mixtures of gases the number of degrees of freedom is the molar average of the degrees of freedom of the pure components.
Q2) Define the term Heat Capacity.
A2)
Suppose that we raise the temperature of the gas by δT without changing its volume. Since no work is performed, and since energy is conserved, the necessary amount of heat is δQ = δU = CVδT where the constant,
CV =  (3)
(3)
The heat capacity at constant volume is what it's termed.
If, on the other hand, the gas pressure is maintained while the temperature is increased, δT, We must also consider that the volume extends by a specific amount V, causing work to be done on the surroundings. This effort has increased the quantity of heat required. δQ= δU+ PδV.
For constant pressure, we can use the ideal gas law. PδV= δ(PV ) = NkδT. As a result, the quantity of heat required per unit of temperature rise at constant pressure is
CP = CV + Nk,(4)
Called the heat capacity at constant pressure. It is always larger than CV because it includes the work of expansion.
Q3) State Isothermal versus isentropic bulk modulus.
A3)
The bulk modulus of a strictly isothermal ideal gas with P = nkT is equal to the pressure,
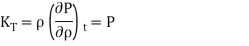
The indicator T indicates that the temperature must be kept constant while we differentiate (in the typical thermodynamic style of writing derivatives). The isentropic condition can be represented in one of three ways in terms of mass density (with three different constants),
Pρ−γ= const,Tρ1−γ= const,TγP1−γ= const.
Using the first we find the isentropic bulk modulus of an ideal gas,

The index S now indicates that the entropy must be maintained constant. In all materials, the distinction between isothermal and isentropic bulk modulus is necessary, though there is little difference between the two for almost incompressible liquids.KS and KT.
The initial computation of the speed of sound in air, using essentially the ideal gas law with constant temperature, was one of Isaac Newton's greatest achievements. Because normal sound waves fluctuate so quickly, compression and expansion are fundamentally isentropic processes, his result did not match the experiment.
Sound travels at a constant pace.

√ such that the ratio between the isentropic and isothermal sound velocities is cS/cT = γ. For air with γ = 1.4 this amounts to an 18% error in the sound velocity. Much later in 1799, Laplace derived the correct value for the speed of sound.
Q4) What are the Specific Quantities in Classical Thermodynamics.
A4)
In classical thermodynamics we always think of a macroscopic volume of matter with the same thermodynamic properties throughout the volume. Volume, mass, energy, entropy, and the specific heats are all extensive quantities, meaning that the amount of any such quantity in a composite system is the sum of the amounts in the parts. Pressure, temperature, and density are in contrast intensive quantities, that may not be added when a system is put together from its parts. In continuum physics, an intensive quantity becomes a field that may vary from place to place, whereas an extensive quantity becomes an integral over the density of the quantity. Since a material particle with a fixed number of molecules has a fixed mass, the natural field to introduce for an extensive quantity like the energy is the specific internal energy u = dU/dM, which is the amount of energy per unit of mass in the neighbourhood of a given point. The actual energy density becomes dU/dV = ρu, and the total energy in a volume

Temperature, pressure, and density are all examples of intense quantities. Similarly, the specific heat is defined as the local heat capacity per unit of mass, which may be written as
u = cVT = 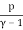
The specific energy of an ideal gas is the specific heat times the absolute temperature.
Q5) Describe Classical Entropy Expression.
A5)
Let us introduce entropy in its classical view, that is how it behaves for macroscopic observers.
The behaviour of entropy can be described by comparison to that of energy. Energy can be transferred between systems but is always globally preserved. In some kinds of processes, entropy can be transferred between systems but is preserved, like energy. These processes are called reversible, which means that they can take place backwards as well, symmetrically with respect to time. Some other processes happen to be created some entropy (its total amount increases). But no process can ever eliminate entropy, which is why the processes that create it are irreversible.
This approach by macroscopic physics (= of human scale, or generally non-microscopic scales ; unfortunately the only one presented in many courses of thermodynamics) remains unsatisfactory as it lets the nature of entropy, its creation process and its irreversibility, looking like mysteries.
In the fundamental laws (quantum physics without measurement) that describe elementary (microscopic) processes, entropy has a clear definition, but all processes are reversible, so that this defined entropy is preserved. Thus, the process of entropy creation is understood as an emergent process, that "occurs" only relatively to the approximation of how things can be summed up in practice when they involve rather disordered large groups of particles. This approximation operation affects the conception of effective states of the system at successive times, and thus the successive values of entropy that are calculated from these effective states. Another form of this emergent process of entropy creation will be quantum decoherence, which is the usually required circumstance to qualify a process as a measurement in quantum physics. These deeper explanations of the microscopic definition and creation of entropy, will be presented in the next pages.
Q6) Elaborate the terms Heat and Temperature in Classical Thermodynamics.
A6)
Let us introduce the concept of temperature as a physical quantity, that is positive in most cases in the correct physical sense, i.e. with respect to the true physical zero value, from which the usual conventions of naming temperatures differ by an additive constant: the true physical zero value of temperature, called "absolute zero", corresponds to the conventional figure of -459.67 °F or -273.15 °C. Temperature in Kelvins (K) is defined as respecting this absolute zero, and with the same unit as Celsius degrees (1/100 of the difference between temperatures of fusion and boiling of water under atmospheric pressure).
There is a maximum amount for the entropy of any material system evolving within given limits of volume and energy. A body that reached its maximal amount of entropy within these limits, is said to be in thermal equilibrium, a state often determined by these conditions (material content, volume and energy). To each system in thermal equilibrium, is also attributed another important physical quantity called its temperature, defined as follows.
Entropy is usually not transferred alone, but together with an amount of energy. A mixture of amounts of energy and entropy that can flow from a system to another, is an amount of heat. (Energy and entropy are not like distinct objects that move, but rather like 2-substance fluids "mixing" themselves by diffusion during contacts, and only the resulting variations of amounts on each side matter). Heat can take several forms: either direct contact or radiation.
The ratio energy/entropy of an amount of heat, is called its temperature.
The temperature of a system in a state of thermal equilibrium, is the temperature of the small amounts of heat that it is ready to transfer to or from the outside, evolving between states of thermal equilibrium of nearby temperatures. Precisely, temperature is defined as the differential (during heat exchanges as the system follows a smooth, reversible change between thermal equilibrium states),
T = δQ/dS
Where
• S = entropy (contained in the system)
• δQ = energy of received heat, = dE + PdV where E = energy, P = pressure, V = volume.
In this way, the variations dE of energy, dS of entropy and dV of volume, of a system with temperature T during (reversible) transfer of a small amount of heat at the same temperature, are related by
DE = TdS − PdV .
Where TdS is the energy received from heat and − PdV is the energy received from the work of pressure.
Metaphorically, the properties of heat and temperature can be compared to the idea of a garbage market with negative prices : the dictionary is
Thermodynamics | Garbage market |
Entropy | Mass of garbage |
Energy | Money |
−temperature | Negative price of garbage |
As the flow of heat must preserve energy but can create entropy, it can only go from "warm" objects (with higher temperature, decreasing their entropy by a smaller amount for the transferred energy) to "cold" ones (with lower temperature, getting more entropy for this energy). This amount of heat increases its entropy when reaching the object with lower temperature.
Usually, any transfer of entropy between systems has a cost: it is an irreversible process, which itself creates more entropy. For example, near a given temperature, flows of heat are roughly proportional to the difference of temperature between bodies. To make them faster, the difference of temperature must increase, so that the transfer creates more entropy. Or, a release of heat makes the environment temporarily warmer, which makes this release more costly. This cost can be reduced (approaching reversibility) by slowing down the transfer.
Heat flows from the warm to the cold by the fact that warm bodies send their heat faster than cold ones. So, heat transfer is faster at higher temperatures, already in terms of energy, but also usually in terms of entropy (a possibility of speed that can be traded with the fact of producing less entropy). In particular, the radiation from warmer objects has both more energy and more entropy, as we shall see below. In the limit, pure energy (that can be seen as heat with infinite temperature) can often be transferred reversibly.
Q7) Describe The entropy in the Universe according to Classical Enthropy Expression.
A7)
For example, life on Earth involves many irreversible processes, which continuously create entropy. As there is a limit in the amount of entropy that can be contained in given limits of volume and energy, the stability of this quantity around average values far below this maximum (to let life continue) is made possible by the continuous transfer of the created entropy from Earth to outer space, in the form of infrared radiation (which carries quite more entropy than sunlight in proportion to its amount of energy because it is colder).
This radiation then crosses interstellar space and mainly ends up in intergalactic space. Thus, the development of life is fed not only by sunlight energy (heat with high temperature) but also by the ever larger and colder intergalactic space, which the universal expansion provides like a huge bin for entropy. Both are complementary, like two markets with different prices provide an opportunity for profit by trade between them.
Still, all the entropy of visible and infrared light from stars and planets, is only a tiny part of the entropy in the universe. Among electromagnetic radiations alone, the cosmic microwave background already has comparable energy to visible and infrared light (1); and thus much more entropy (ignoring the entropy of practically undetectable particles: dark matter, neutrinos, gravitons...).
But most of the entropy of the universe is made of the giant black holes in galactic centers. Indeed, the fall of matter into black holes, contributing to the growth of their size and thus of their entropy (proportional to the area of their horizon), is among the most radically irreversible processes of the Universe (that will only be "reversed" after very unreasonable times by "evaporation" in a much, much colder universe...)
Q8) Define the Physical units of temperature and entropy.
A8)
In the ideal gas law, the gas constant R=8.314 J mol−1K−1, is the natural conversion constant by which the temperature T (expressed in Kelvin), in the form of the product RT, is physically involved as a composite of other physical quantities. This gas constant is never far from any phenomenon involving temperature, even for solids instead of gases, so that temperature (and thus entropy) only conventionally has its own unit, while its true physical nature is that of a composite of other physical quantities.
Namely, the ideal gas law presents the physically meaningful expression RT of the temperature, as an energy per amount of substance (which explains the units involved in the value of R). It also reduces entropy (initially expressed in J/K) as comparable with an amount of substance.
Microscopically, moles are replaced by numbers of molecules, so that the conversion factor is the Boltzmann constant k= R/NA:
a temperature T microscopically appears as a typical amount of energy E=kT, while an amount of entropy S becomes a real number S/k.
This naturally suggests that the variations of temperature of a given object would be proportional to the transferred amounts of heat energy.
Q9) What is Entropy of Mixing, and Gibbs' Paradox.
A9)
We defined the increase of entropy of a system by supposing that an infinitesimal quantity dQ of heat is added to it at temperature T, and that no irreversible work is done on the system. We then asserted that the increase of entropy of the system is dS = dQ/T. If some irreversible work is done, this has to be added to the dQ.
We also pointed out that, in an isolated system any spontaneous transfer of heat from one part to another part was likely (very likely!) to be from a hot region to a cooler region, and that this was likely (very likely!) to result in an increase of entropy of the closed system − indeed of the Universe. We considered a box divided into two parts, with a hot gas in one and a cooler gas in the other, and we discussed what was likely (very likely!) to happen if the wall between the parts were to be removed. We considered also the situation in which the wall were to separate two gases consisting or red molecules and blue molecules. The two situations seem to be very similar. A flow of heat is not the flow of an “imponderable fluid” called “caloric”. Rather it is the mixing of two groups of molecules with initially different characteristics (“fast” and “slow”, or “hot” and “cold”). In either case there is likely (very likely!) to be a spontaneous mixing, or increasing randomness, or increasing disorder or increasing entropy. Seen thus, entropy is seen as a measure of the degree of disorder. In this section we are going to calculate the increase on entropy when two different sorts of molecules become mixed, without any reference to the flow of heat. This concept of entropy as a measure of disorder will become increasingly apparent if you undertake a study of statistical mechanics.
Consider a box containing two gases, separated by a partition. The pressure and temperature are the same in both compartments. The left hand compartment contains N1 moles of gas 1, and the right hand compartment contains N2 moles of gas 2. The Gibbs function for the system is
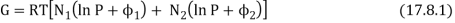
Remove the divider and wait until the gases are thoroughly mixed with no pressure or temperature change. Gas 1's partial molar Gibbs function is

And the partial molar Gibbs function of gas 2 is

Here the pi are the partial pressures of the two gases, given by and p1 = n1P, p2 = n2P where the ni are the mole fractions.
The total Gibbs function is now N1µ1 + N2µ2, or
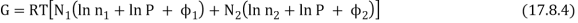
As a result, the new Gibbs function is equal to the old Gibbs function.
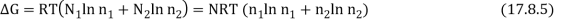
Because the mole fractions are fewer than 1, this results in a drop in the Gibbs function.
The new entropy minus the original entropy is ΔS=−[∂(ΔG)∂T]P, which is

This is positive, because the mole fractions are less than 1.
Similar expressions will be obtained for the increase in entropy if we mix several gases.
Here’s maybe an easier way of looking at the same thing. (Remember that, in what follows, the mixing is presumed to be ideal and the temperature and pressure are constant throughout.)
Q10) Write a short note on Sackur Tetrode equation.
A10)
The Sackur-Tetrode equation is important historically, because it suggests quantization (and a value for Planck’s constant h) based solely on experimental work in thermodynamics. The result provides a basis for quantum theory that is independent of Planck’s first conception of it, which he developed in the theory of blackbody radiation, and from Einstein’s conception of quantization based on the photoelectric effect.
The Sackur–Tetrode equation is an expression for the entropy of a monatomic classical ideal gas which incorporates quantum considerations which give a more detailed description of its regime of validity. The Sackur–Tetrode equation is named for Hugo Martin Tetrode (1895– 1931) and Otto Sackur (1880–1914), who developed it independently as a solution of Boltzmann's gas statistics and entropy equations, at about the same time in 1912. Now we calculate the partition function (canonical ensemble) using the density of state for the one particle system
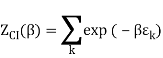
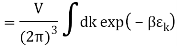
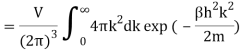
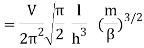

Q11) State the Law Of Equi-partition of Energy.
A11)
According to the law of equipartition of energy, for any dynamic system in thermal equilibrium, the total energy for the system is equally divided among the degree of freedom.
The kinetic energy of a single molecule along the x-axis, the y-axis, and the z-axis is given as
1/2m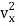 along the x-axis
along the x-axis
1/2m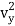 , along the y-axis
, along the y-axis
1/2m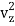 , along the z-axis
, along the z-axis
When the gas is at thermal equilibrium, the average kinetic energy is denoted as
(1/2m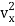 ), along the x-axis
), along the x-axis
(1/2m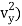 , along the y-axis
, along the y-axis
(1/2m , along the z-axis
, along the z-axis
The average kinetic energy of a molecule is determined by, according to the kinetic theory of gases.
½ m vrms2 = 3/2 Kb T
Where Vrms is the root-mean-square velocity of the molecules, Kb is the Boltzmann constant and T is the temperature of the gas.
Because there are three degrees of freedom in a monoatomic gas, the average kinetic energy per degree of freedom is given by KEx = ½ KbT
If a molecule is free to move in space, it requires three coordinates to indicate its location, implying that it has three degrees of freedom in translation. It has two translational degrees of freedom if it is confined to travel in a plane, and one translational degree of freedom if it is bound to travel in a straight line. The degree of freedom in the instance of a triatomic molecule is 6. And the per-molecule kinetic energy of the gas is given as,
6 × N × ½ Kb T = 3 × R/N N Kb T = 3RT
Q12) Explain the Application of law of equi-partition energy in specific heat of a gas.
A12)
Meyer’s relation CP − CV = R connects the two specific heats for one mole of an ideal gas.
Equipartition law of energy is used to calculate the value of CP − CV and the ratio between them γ = CP / CV.
Here γ is called adiabatic exponent.
i) Monatomic molecule
Average kinetic energy of a molecule
=[ 3/2 kT]
Total energy of a mole of gas
= 3/2 kT × NA = 3/2 RT
For one mole, the molar specific heat at constant volume


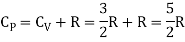
The ratio of specific heats,
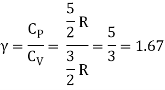
Ii) Diatomic molecule
Average kinetic energy of a diatomic molecule at low temperature = 5/2kT
Total energy of one mole of gas
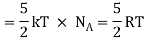
(Here, the total energy is purely kinetic)
For one mole Specific heat at constant volume
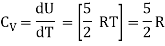
But 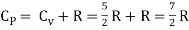
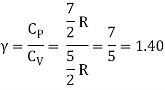
Energy of a diatomic molecule at high temperature is equal to 7/2RT

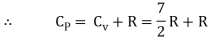
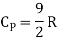
Note that the CV and CP are higher for diatomic molecules than the mono atomic molecules. It implies that to increase the temperature of diatomic gas molecules by 1°C it require more heat energy than monoatomic molecules.
Iii) Triatomic molecule
a) Linear molecule
Energy of one mole = 7/2 kT × NA = 7/2 RT
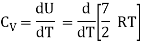
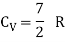


b) Non-linear molecule
Energy of a mole = 6/2 kT × NA = 6/2 RT = 3 RT



Note that according to kinetic theory model of gases the specific heat capacity at constant volume and constant pressure are independent of temperature. But in reality it is not sure. The specific heat capacity varies with the temperature
Q13) What is Partition Function for Two Level System.
A13)
I have a system with Ns sites and N particles, such that Ns>>N>>1. If a site has no particle, then there is zero energy associated with that site. The N particles occupy the Ns sites and can be in energies E1 or E0, where E1>E0. We also know mm particles have energy E1 and N−mN−m have particles E0.
I'm trying to come up with the partition function for this system.
I found the total energy so far to be E = mE1 + (N – m) E0. I know the partition function is 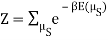 , where μs sums over all the possible microstates.
, where μs sums over all the possible microstates.
I'm trying to use the formula:
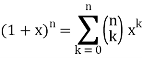
Can someone show me how this is done?
I've also figured out there are 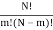 ways of getting m, E1 states and N – m, E0, states and
ways of getting m, E1 states and N – m, E0, states and 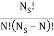 ways of arranging the N particles in the Ns sites.
ways of arranging the N particles in the Ns sites.
Following the advice of the nephente, this is what I get so far:
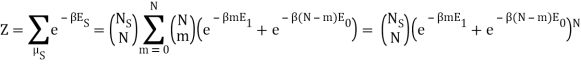
Because the particle may have energy E1 or E0, I assumed there would be a total of two exponentials. Are you suggesting that we just have:

What about the zero-point energy E0? I'm having trouble figuring out which one is correct, and I'm not sure why the sum over millimetres is required. Mm was supposed to be fixed, right?
Here, I am thinking of  as the degeneracy for each microstate due to arranging the N particles in Ns sites.
as the degeneracy for each microstate due to arranging the N particles in Ns sites.
Q14) Explain the term Temperature according to Negative Temperature.
A14)
To get things started, we need a clear definition of "temperature." Actually various kinds of "temperature" appear in the literature of physics (e.g., kinetic temperature, color temperature). The relevant one here is the one from thermodynamics, in some sense the most fundamental.
Our intuitive notion is that two systems in thermal contact should exchange no heat, on average, if and only if they are at the same temperature. Let's call the two systems S1 and S2. The combined system, treating S1 and S2 together, can be S3. The important question, consideration of which will lead us to a useful quantitative definition of temperature, is "How will the energy of S3 be distributed between S1 and S2?" I will briefly explain this below, but I recommend that you read K&K, referenced below, for a careful, simple, and thorough explanation of this important and fundamental result.
With a total energy E, S has many possible internal states (microstates). The atoms of S3 can share the total energy in many ways. Let's say there are N different states. Each state corresponds to a particular division of the total energy in the two subsystems S1 and S2. Many microstates can correspond to the same division, E1 in S1 and E2 in S2. A simple counting argument tells you that only one particular division of the energy, will occur with any significant probability. It's the one with the overwhelmingly largest number of microstates for the total system S3. That number, N(E1,E2) is just the product of the number of states allowed in each subsystem, N(E1,E2) = N1(E1)*N2(E2), and, since E1 + E2 = E, N(E1,E2) reaches a maximum when N1*N2 is stationary with respect to variations of E1 and E2 subject to the total energy constraint.
For convenience, physicists prefer to frame the question in terms of the logarithm of the number of microstates N, and call this the entropy, S. You can easily see from the above analysis that two systems are in equilibrium with one another when (dS/dE)1 = (dS/dE)2, i.e., the rate of change of entropy, S, per unit change in energy, E, must be the same for both systems. Otherwise, energy will tend to flow from one subsystem to another as S3 bounces randomly from one microstate to another, the total energy E3 being constant, as the combined system moves towards a state of maximal total entropy. We define the temperature, T, by 1/T = dS/dE, so that the equilibrium condition becomes the very simple T1 = T2.
This statistical mechanical definition of temperature does in fact correspond to your intuitive notion of temperature for most systems. So long as dS/dE is always positive, T is always positive. For common situations, like a collection of free particles, or particles in a harmonic oscillator potential, adding energy always increases the number of available microstates, increasingly faster with increasing total energy. So temperature increases with increasing energy, from zero, asymptotically approaching positive infinity as the energy increases.
Q15) What is "Negative Temperature"?
A15)
Not all systems have the property that the entropy increases monotonically with energy. In some cases, as energy is added to the system, the number of available microstates, or configurations, actually decreases for some range of energies. For example, imagine an ideal "spin-system", a set of N atoms with spin 1/2 on a one-dimensional wire. The atoms are not free to move from their positions on the wire. The only degree of freedom allowed to them is spin-flip: the spin of a given atom can point up or down. The total energy of the system, in a magnetic field of strength B, pointing down, is (N+ - N-)*uB, where u is the magnetic moment of each atom and N+ and N- are the number of atoms with spin up and down respectively. Notice that with this definition, E is zero when half of the spins are up and half are down. It is negative when the majority are down and positive when the majority are up.
The lowest possible energy state, all the spins pointing down, gives the system a total energy of -NuB, and temperature of absolute zero. There is only one configuration of the system at this energy, i.e., all the spins must point down. The entropy is the log of the number of microstates, so in this case is log(1) = 0. If we now add a quantum of energy, size uB, to the system, one spin is allowed to flip up. There are N possibilities, so the entropy is log(N). If we add another quantum of energy, there are a total of N(N-1)/2 allowable configurations with two spins up. The entropy is increasing quickly, and the temperature is rising as well.
However, for this system, the entropy does not go on increasing forever. There is a maximum energy, +NuB, with all spins up. At this maximal energy, there is again only one microstate, and the entropy is again zero. If we remove one quantum of energy from the system, we allow one spin down. At this energy there are N available microstates. The entropy goes on increasing as the energy is lowered. In fact the maximal entropy occurs for total energy zero, i.e., half of the spins up, half down.
So we have created a system where, as we add more and more energy, temperature starts off positive, approaches positive infinity as maximum entropy is approached, with half of all spins up. After that, the temperature becomes negative infinite, coming down in magnitude toward zero, but always negative, as the energy increases toward maximum. When the system has negative temperature, it is hotter than when it is has positive temperature. If you take two copies of the system, one with positive and one with negative temperature, and put them in thermal contact, heat will flow from the negative-temperature system into the positive-temperature system.
Q16) Enlist and explain any 2 molecular terms from Application of law of equi-partition energy in specific heat of a gas.
A16)
i) Monatomic molecule
Average kinetic energy of a molecule
=[ 3/2 kT]
Total energy of a mole of gas
= 3/2 kT × NA = 3/2 RT
For one mole, the molar specific heat at constant volume
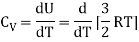
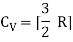

The ratio of specific heats,
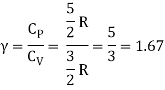
Ii) Diatomic molecule
Average kinetic energy of a diatomic molecule at low temperature = 5/2kT
Total energy of one mole of gas

(Here, the total energy is purely kinetic)
For one mole Specific heat at constant volume
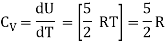
But 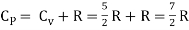
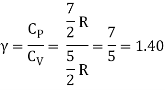
Energy of a diatomic molecule at high temperature is equal to 7/2RT
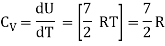
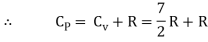
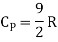
Note that the CV and CP are higher for diatomic molecules than the mono atomic molecules. It implies that to increase the temperature of diatomic gas molecules by 1°C it require more heat energy than monoatomic molecules.

Iii) Triatomic molecule
c) Linear molecule
Energy of one mole = 7/2 kT × NA = 7/2 RT


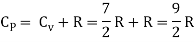
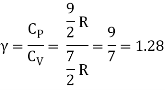
Q17) Define the Amounts of substance according to The Classical Entropy.
A17)
To express the behaviors of temperature and entropy quantitatively, we need to relate them with other physical quantities. Precisely, amounts of entropy happen to be essentially convertible into amounts of substance. Let us first explain what is this.
The amount of substance counts the very large number of atoms or molecules contained in macroscopic objects. Thus its deep meaning is that of natural numbers, but too big for the unit number (an individual atom or molecule) to be of any significance.
This concept comes from chemistry, as chemical reactions involve ingredients in precise proportions to form molecules containing the right numbers of atoms (this was first an observed fact at the beginning of the 19th century, until its explanation in terms of atoms was clearly established later that century).
The conventional unit for amounts of substance is the mol: 1 mol means NA molecules, where the number NA≈ 6.022×1023 is the Avogadro constant. Thus, n mol of some pure substance contains n×N A molecules of this substance.
This number comes from the choice that 1 mol of Carbon-12 weights 12 grams (thus roughly, 1 mol of hydrogen atoms weights 1 gram = 0.001 kg, with a slight difference due to the nuclear binding energy, converted into mass by E=mc2).
It can be seen as quantity NA ≈ 6.022×1023 mol-1.
Q18) Describe the Isentropic processes.
A18)
Any process in an open system which does not exchange heat with the environment is said to be adiabatic. If the process is furthermore reversible, it follows that ∂Q = 0 in each infinitesimal step, so that the ∂S = ∂Q/T = 0. The entropy must in other words stay constant in any reversible, adiabatic process. Such a process is for this reason called isentropic. By means of the adiabatic index we may write the entropy as,
S = CV log(TV γ−1) + const,(10)
From this it follows that
TV γ−1 = const,(11)
For any isentropic process in an ideal gas. Using the ideal gas law to eliminate V ∼ T/P, this may be written equivalently as,
TγP1−γ = const.(12)
Eliminating instead T ∼ PV , the isentropic condition takes its most common form,
PV γ = const.(13)
Q19) Define the two fundamental laws of thermodynamics.
A19)
The reason is that the two fundamental laws of thermodynamics are formulated in terms of the energy and the entropy. Both laws concern processes that may take place in an isolated system which is not allowed to exchange heat with or perform work on the environment. The First Law states that the energy is unchanged under any process in an isolated system. This implies that the energy of an open system can only change by exchange of heat or work with the environment. We actually used this law implicitly in deriving the heat capacities and the entropy. The Second Law states that the entropy cannot decrease. In the real world, the entropy of an isolated system must in fact grow. Only if all the processes taking place in the system are completely reversible at all times, will the entropy stay constant. Reversibility is an ideal which can only be approached by very slow quasistatic processes, consisting of infinitely many infinitesimal reversible steps. Essentially all real-world processes are irreversible to some degree.
Q20) What is Entropy?
A20)
When neither the volume nor the pressure are kept constant, the heat that must be added to the system in an infinitesimal process is,
δQ = ∂U + PδV = CV δ T + Nk T δV/V
It is a mathematical fact that there exists no function, Q(T,V ), which has this expression as differential. It may on the other hand be directly verified (by insertion) that
δS = δQ/T + CV δT/T + NK δV/V
Can be integrated to yield a function,
S = CV logT + Nk logV + c,
Called the entropy of the amount of ideal gas. Being an integral the entropy is only defined up to an arbitrary constant. The entropy of the gas is, like its energy, an abstract quantity which cannot be directly measured. But since both quantities depend on the measurable thermodynamic quantities that characterize the state of the gas, we can calculate the value of energy and entropy in any state.
Unit - 2
Classical Statistics - II
Q1) Explain the term Internal Energy.
A1)
Using the ideal gas law, the total molecular kinetic energy contained in an amount M = ρV of the gas becomes,
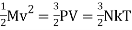 (1)
(1)
The factor 3 stems from the three independent translational degrees of freedom available to point like particles. The above formula thus expresses that there is an internal kinetic energy ½ kT associated with each translational degree of freedom. Whereas monatomic gases like Argon have spherical molecules and thus only the three translational degrees of freedom, diatomic gases like nitrogen and oxygen have stick-like molecules with two extra rotational degrees of freedom orthogonally to the bridge connecting the atoms, and multi-atomic gases like carbon dioxide and methane have the three extra rotational degrees of freedom. According to the equipartition theorem of statistical mechanics these degrees of freedom will also carry a kinetic energy ½ kT per particle. Molecules also possess vibrational degrees of freedom that may become excited, but we shall disregard them here. The internal energy of N particles of an ideal gas is defined to be,
βU =NkT,(2)
Where β is the number of degrees of freedom. Physically a gas may dissociate or even ionize when heated, and thereby change its value of β, but we shall for simplicity assume that β is in fact constant with β = 3 for monatomic, β = 5 for diatomic, and β = 6 for multiatomic gases. For mixtures of gases the number of degrees of freedom is the molar average of the degrees of freedom of the pure components.
Q2) Define the term Heat Capacity.
A2)
Suppose that we raise the temperature of the gas by δT without changing its volume. Since no work is performed, and since energy is conserved, the necessary amount of heat is δQ = δU = CVδT where the constant,
CV = 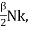 (3)
(3)
The heat capacity at constant volume is what it's termed.
If, on the other hand, the gas pressure is maintained while the temperature is increased, δT, We must also consider that the volume extends by a specific amount V, causing work to be done on the surroundings. This effort has increased the quantity of heat required. δQ= δU+ PδV.
For constant pressure, we can use the ideal gas law. PδV= δ(PV ) = NkδT. As a result, the quantity of heat required per unit of temperature rise at constant pressure is
CP = CV + Nk,(4)
Called the heat capacity at constant pressure. It is always larger than CV because it includes the work of expansion.
Q3) State Isothermal versus isentropic bulk modulus.
A3)
The bulk modulus of a strictly isothermal ideal gas with P = nkT is equal to the pressure,

The indicator T indicates that the temperature must be kept constant while we differentiate (in the typical thermodynamic style of writing derivatives). The isentropic condition can be represented in one of three ways in terms of mass density (with three different constants),
Pρ−γ= const,Tρ1−γ= const,TγP1−γ= const.
Using the first we find the isentropic bulk modulus of an ideal gas,

The index S now indicates that the entropy must be maintained constant. In all materials, the distinction between isothermal and isentropic bulk modulus is necessary, though there is little difference between the two for almost incompressible liquids.KS and KT.
The initial computation of the speed of sound in air, using essentially the ideal gas law with constant temperature, was one of Isaac Newton's greatest achievements. Because normal sound waves fluctuate so quickly, compression and expansion are fundamentally isentropic processes, his result did not match the experiment.
Sound travels at a constant pace.

√ such that the ratio between the isentropic and isothermal sound velocities is cS/cT = γ. For air with γ = 1.4 this amounts to an 18% error in the sound velocity. Much later in 1799, Laplace derived the correct value for the speed of sound.
Q4) What are the Specific Quantities in Classical Thermodynamics.
A4)
In classical thermodynamics we always think of a macroscopic volume of matter with the same thermodynamic properties throughout the volume. Volume, mass, energy, entropy, and the specific heats are all extensive quantities, meaning that the amount of any such quantity in a composite system is the sum of the amounts in the parts. Pressure, temperature, and density are in contrast intensive quantities, that may not be added when a system is put together from its parts. In continuum physics, an intensive quantity becomes a field that may vary from place to place, whereas an extensive quantity becomes an integral over the density of the quantity. Since a material particle with a fixed number of molecules has a fixed mass, the natural field to introduce for an extensive quantity like the energy is the specific internal energy u = dU/dM, which is the amount of energy per unit of mass in the neighbourhood of a given point. The actual energy density becomes dU/dV = ρu, and the total energy in a volume

Temperature, pressure, and density are all examples of intense quantities. Similarly, the specific heat is defined as the local heat capacity per unit of mass, which may be written as
u = cVT = 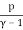
The specific energy of an ideal gas is the specific heat times the absolute temperature.
Q5) Describe Classical Entropy Expression.
A5)
Let us introduce entropy in its classical view, that is how it behaves for macroscopic observers.
The behaviour of entropy can be described by comparison to that of energy. Energy can be transferred between systems but is always globally preserved. In some kinds of processes, entropy can be transferred between systems but is preserved, like energy. These processes are called reversible, which means that they can take place backwards as well, symmetrically with respect to time. Some other processes happen to be created some entropy (its total amount increases). But no process can ever eliminate entropy, which is why the processes that create it are irreversible.
This approach by macroscopic physics (= of human scale, or generally non-microscopic scales ; unfortunately the only one presented in many courses of thermodynamics) remains unsatisfactory as it lets the nature of entropy, its creation process and its irreversibility, looking like mysteries.
In the fundamental laws (quantum physics without measurement) that describe elementary (microscopic) processes, entropy has a clear definition, but all processes are reversible, so that this defined entropy is preserved. Thus, the process of entropy creation is understood as an emergent process, that "occurs" only relatively to the approximation of how things can be summed up in practice when they involve rather disordered large groups of particles. This approximation operation affects the conception of effective states of the system at successive times, and thus the successive values of entropy that are calculated from these effective states. Another form of this emergent process of entropy creation will be quantum decoherence, which is the usually required circumstance to qualify a process as a measurement in quantum physics. These deeper explanations of the microscopic definition and creation of entropy, will be presented in the next pages.
Q6) Elaborate the terms Heat and Temperature in Classical Thermodynamics.
A6)
Let us introduce the concept of temperature as a physical quantity, that is positive in most cases in the correct physical sense, i.e. with respect to the true physical zero value, from which the usual conventions of naming temperatures differ by an additive constant: the true physical zero value of temperature, called "absolute zero", corresponds to the conventional figure of -459.67 °F or -273.15 °C. Temperature in Kelvins (K) is defined as respecting this absolute zero, and with the same unit as Celsius degrees (1/100 of the difference between temperatures of fusion and boiling of water under atmospheric pressure).
There is a maximum amount for the entropy of any material system evolving within given limits of volume and energy. A body that reached its maximal amount of entropy within these limits, is said to be in thermal equilibrium, a state often determined by these conditions (material content, volume and energy). To each system in thermal equilibrium, is also attributed another important physical quantity called its temperature, defined as follows.
Entropy is usually not transferred alone, but together with an amount of energy. A mixture of amounts of energy and entropy that can flow from a system to another, is an amount of heat. (Energy and entropy are not like distinct objects that move, but rather like 2-substance fluids "mixing" themselves by diffusion during contacts, and only the resulting variations of amounts on each side matter). Heat can take several forms: either direct contact or radiation.
The ratio energy/entropy of an amount of heat, is called its temperature.
The temperature of a system in a state of thermal equilibrium, is the temperature of the small amounts of heat that it is ready to transfer to or from the outside, evolving between states of thermal equilibrium of nearby temperatures. Precisely, temperature is defined as the differential (during heat exchanges as the system follows a smooth, reversible change between thermal equilibrium states),
T = δQ/dS
Where
• S = entropy (contained in the system)
• δQ = energy of received heat, = dE + PdV where E = energy, P = pressure, V = volume.
In this way, the variations dE of energy, dS of entropy and dV of volume, of a system with temperature T during (reversible) transfer of a small amount of heat at the same temperature, are related by
DE = TdS − PdV .
Where TdS is the energy received from heat and − PdV is the energy received from the work of pressure.
Metaphorically, the properties of heat and temperature can be compared to the idea of a garbage market with negative prices : the dictionary is
Thermodynamics | Garbage market |
Entropy | Mass of garbage |
Energy | Money |
−temperature | Negative price of garbage |
As the flow of heat must preserve energy but can create entropy, it can only go from "warm" objects (with higher temperature, decreasing their entropy by a smaller amount for the transferred energy) to "cold" ones (with lower temperature, getting more entropy for this energy). This amount of heat increases its entropy when reaching the object with lower temperature.
Usually, any transfer of entropy between systems has a cost: it is an irreversible process, which itself creates more entropy. For example, near a given temperature, flows of heat are roughly proportional to the difference of temperature between bodies. To make them faster, the difference of temperature must increase, so that the transfer creates more entropy. Or, a release of heat makes the environment temporarily warmer, which makes this release more costly. This cost can be reduced (approaching reversibility) by slowing down the transfer.
Heat flows from the warm to the cold by the fact that warm bodies send their heat faster than cold ones. So, heat transfer is faster at higher temperatures, already in terms of energy, but also usually in terms of entropy (a possibility of speed that can be traded with the fact of producing less entropy). In particular, the radiation from warmer objects has both more energy and more entropy, as we shall see below. In the limit, pure energy (that can be seen as heat with infinite temperature) can often be transferred reversibly.
Q7) Describe The entropy in the Universe according to Classical Enthropy Expression.
A7)
For example, life on Earth involves many irreversible processes, which continuously create entropy. As there is a limit in the amount of entropy that can be contained in given limits of volume and energy, the stability of this quantity around average values far below this maximum (to let life continue) is made possible by the continuous transfer of the created entropy from Earth to outer space, in the form of infrared radiation (which carries quite more entropy than sunlight in proportion to its amount of energy because it is colder).
This radiation then crosses interstellar space and mainly ends up in intergalactic space. Thus, the development of life is fed not only by sunlight energy (heat with high temperature) but also by the ever larger and colder intergalactic space, which the universal expansion provides like a huge bin for entropy. Both are complementary, like two markets with different prices provide an opportunity for profit by trade between them.
Still, all the entropy of visible and infrared light from stars and planets, is only a tiny part of the entropy in the universe. Among electromagnetic radiations alone, the cosmic microwave background already has comparable energy to visible and infrared light (1); and thus much more entropy (ignoring the entropy of practically undetectable particles: dark matter, neutrinos, gravitons...).
But most of the entropy of the universe is made of the giant black holes in galactic centers. Indeed, the fall of matter into black holes, contributing to the growth of their size and thus of their entropy (proportional to the area of their horizon), is among the most radically irreversible processes of the Universe (that will only be "reversed" after very unreasonable times by "evaporation" in a much, much colder universe...)
Q8) Define the Physical units of temperature and entropy.
A8)
In the ideal gas law, the gas constant R=8.314 J mol−1K−1, is the natural conversion constant by which the temperature T (expressed in Kelvin), in the form of the product RT, is physically involved as a composite of other physical quantities. This gas constant is never far from any phenomenon involving temperature, even for solids instead of gases, so that temperature (and thus entropy) only conventionally has its own unit, while its true physical nature is that of a composite of other physical quantities.
Namely, the ideal gas law presents the physically meaningful expression RT of the temperature, as an energy per amount of substance (which explains the units involved in the value of R). It also reduces entropy (initially expressed in J/K) as comparable with an amount of substance.
Microscopically, moles are replaced by numbers of molecules, so that the conversion factor is the Boltzmann constant k= R/NA:
a temperature T microscopically appears as a typical amount of energy E=kT, while an amount of entropy S becomes a real number S/k.
This naturally suggests that the variations of temperature of a given object would be proportional to the transferred amounts of heat energy.
Q9) What is Entropy of Mixing, and Gibbs' Paradox.
A9)
We defined the increase of entropy of a system by supposing that an infinitesimal quantity dQ of heat is added to it at temperature T, and that no irreversible work is done on the system. We then asserted that the increase of entropy of the system is dS = dQ/T. If some irreversible work is done, this has to be added to the dQ.
We also pointed out that, in an isolated system any spontaneous transfer of heat from one part to another part was likely (very likely!) to be from a hot region to a cooler region, and that this was likely (very likely!) to result in an increase of entropy of the closed system − indeed of the Universe. We considered a box divided into two parts, with a hot gas in one and a cooler gas in the other, and we discussed what was likely (very likely!) to happen if the wall between the parts were to be removed. We considered also the situation in which the wall were to separate two gases consisting or red molecules and blue molecules. The two situations seem to be very similar. A flow of heat is not the flow of an “imponderable fluid” called “caloric”. Rather it is the mixing of two groups of molecules with initially different characteristics (“fast” and “slow”, or “hot” and “cold”). In either case there is likely (very likely!) to be a spontaneous mixing, or increasing randomness, or increasing disorder or increasing entropy. Seen thus, entropy is seen as a measure of the degree of disorder. In this section we are going to calculate the increase on entropy when two different sorts of molecules become mixed, without any reference to the flow of heat. This concept of entropy as a measure of disorder will become increasingly apparent if you undertake a study of statistical mechanics.
Consider a box containing two gases, separated by a partition. The pressure and temperature are the same in both compartments. The left hand compartment contains N1 moles of gas 1, and the right hand compartment contains N2 moles of gas 2. The Gibbs function for the system is
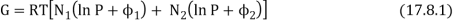
Remove the divider and wait until the gases are thoroughly mixed with no pressure or temperature change. Gas 1's partial molar Gibbs function is

And the partial molar Gibbs function of gas 2 is

Here the pi are the partial pressures of the two gases, given by and p1 = n1P, p2 = n2P where the ni are the mole fractions.
The total Gibbs function is now N1µ1 + N2µ2, or
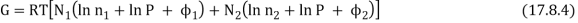
As a result, the new Gibbs function is equal to the old Gibbs function.
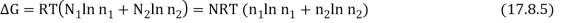
Because the mole fractions are fewer than 1, this results in a drop in the Gibbs function.
The new entropy minus the original entropy is ΔS=−[∂(ΔG)∂T]P, which is

This is positive, because the mole fractions are less than 1.
Similar expressions will be obtained for the increase in entropy if we mix several gases.
Here’s maybe an easier way of looking at the same thing. (Remember that, in what follows, the mixing is presumed to be ideal and the temperature and pressure are constant throughout.)
Q10) Write a short note on Sackur Tetrode equation.
A10)
The Sackur-Tetrode equation is important historically, because it suggests quantization (and a value for Planck’s constant h) based solely on experimental work in thermodynamics. The result provides a basis for quantum theory that is independent of Planck’s first conception of it, which he developed in the theory of blackbody radiation, and from Einstein’s conception of quantization based on the photoelectric effect.
The Sackur–Tetrode equation is an expression for the entropy of a monatomic classical ideal gas which incorporates quantum considerations which give a more detailed description of its regime of validity. The Sackur–Tetrode equation is named for Hugo Martin Tetrode (1895– 1931) and Otto Sackur (1880–1914), who developed it independently as a solution of Boltzmann's gas statistics and entropy equations, at about the same time in 1912. Now we calculate the partition function (canonical ensemble) using the density of state for the one particle system



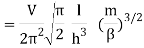

Q11) State the Law Of Equi-partition of Energy.
A11)
According to the law of equipartition of energy, for any dynamic system in thermal equilibrium, the total energy for the system is equally divided among the degree of freedom.
The kinetic energy of a single molecule along the x-axis, the y-axis, and the z-axis is given as
1/2m along the x-axis
along the x-axis
1/2m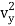 , along the y-axis
, along the y-axis
1/2m , along the z-axis
, along the z-axis
When the gas is at thermal equilibrium, the average kinetic energy is denoted as
(1/2m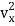 ), along the x-axis
), along the x-axis
(1/2m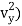 , along the y-axis
, along the y-axis
(1/2m , along the z-axis
, along the z-axis
The average kinetic energy of a molecule is determined by, according to the kinetic theory of gases.
½ m vrms2 = 3/2 Kb T
Where Vrms is the root-mean-square velocity of the molecules, Kb is the Boltzmann constant and T is the temperature of the gas.
Because there are three degrees of freedom in a monoatomic gas, the average kinetic energy per degree of freedom is given by KEx = ½ KbT
If a molecule is free to move in space, it requires three coordinates to indicate its location, implying that it has three degrees of freedom in translation. It has two translational degrees of freedom if it is confined to travel in a plane, and one translational degree of freedom if it is bound to travel in a straight line. The degree of freedom in the instance of a triatomic molecule is 6. And the per-molecule kinetic energy of the gas is given as,
6 × N × ½ Kb T = 3 × R/N N Kb T = 3RT
Q12) Explain the Application of law of equi-partition energy in specific heat of a gas.
A12)
Meyer’s relation CP − CV = R connects the two specific heats for one mole of an ideal gas.
Equipartition law of energy is used to calculate the value of CP − CV and the ratio between them γ = CP / CV.
Here γ is called adiabatic exponent.
i) Monatomic molecule
Average kinetic energy of a molecule
=[ 3/2 kT]
Total energy of a mole of gas
= 3/2 kT × NA = 3/2 RT
For one mole, the molar specific heat at constant volume
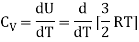
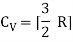

The ratio of specific heats,
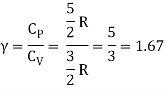
Ii) Diatomic molecule
Average kinetic energy of a diatomic molecule at low temperature = 5/2kT
Total energy of one mole of gas

(Here, the total energy is purely kinetic)
For one mole Specific heat at constant volume

But 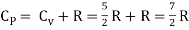
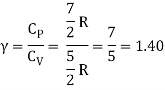
Energy of a diatomic molecule at high temperature is equal to 7/2RT

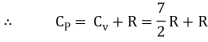
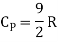
Note that the CV and CP are higher for diatomic molecules than the mono atomic molecules. It implies that to increase the temperature of diatomic gas molecules by 1°C it require more heat energy than monoatomic molecules.
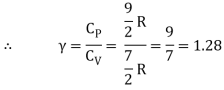
Iii) Triatomic molecule
a) Linear molecule
Energy of one mole = 7/2 kT × NA = 7/2 RT

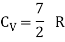

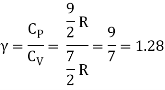
b) Non-linear molecule
Energy of a mole = 6/2 kT × NA = 6/2 RT = 3 RT


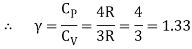
Note that according to kinetic theory model of gases the specific heat capacity at constant volume and constant pressure are independent of temperature. But in reality it is not sure. The specific heat capacity varies with the temperature
Q13) What is Partition Function for Two Level System.
A13)
I have a system with Ns sites and N particles, such that Ns>>N>>1. If a site has no particle, then there is zero energy associated with that site. The N particles occupy the Ns sites and can be in energies E1 or E0, where E1>E0. We also know mm particles have energy E1 and N−mN−m have particles E0.
I'm trying to come up with the partition function for this system.
I found the total energy so far to be E = mE1 + (N – m) E0. I know the partition function is 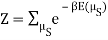 , where μs sums over all the possible microstates.
, where μs sums over all the possible microstates.
I'm trying to use the formula:
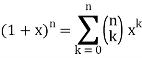
Can someone show me how this is done?
I've also figured out there are 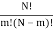 ways of getting m, E1 states and N – m, E0, states and
ways of getting m, E1 states and N – m, E0, states and  ways of arranging the N particles in the Ns sites.
ways of arranging the N particles in the Ns sites.
Following the advice of the nephente, this is what I get so far:
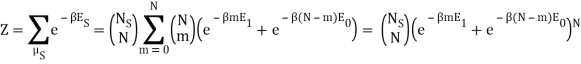
Because the particle may have energy E1 or E0, I assumed there would be a total of two exponentials. Are you suggesting that we just have:

What about the zero-point energy E0? I'm having trouble figuring out which one is correct, and I'm not sure why the sum over millimetres is required. Mm was supposed to be fixed, right?
Here, I am thinking of 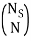 as the degeneracy for each microstate due to arranging the N particles in Ns sites.
as the degeneracy for each microstate due to arranging the N particles in Ns sites.
Q14) Explain the term Temperature according to Negative Temperature.
A14)
To get things started, we need a clear definition of "temperature." Actually various kinds of "temperature" appear in the literature of physics (e.g., kinetic temperature, color temperature). The relevant one here is the one from thermodynamics, in some sense the most fundamental.
Our intuitive notion is that two systems in thermal contact should exchange no heat, on average, if and only if they are at the same temperature. Let's call the two systems S1 and S2. The combined system, treating S1 and S2 together, can be S3. The important question, consideration of which will lead us to a useful quantitative definition of temperature, is "How will the energy of S3 be distributed between S1 and S2?" I will briefly explain this below, but I recommend that you read K&K, referenced below, for a careful, simple, and thorough explanation of this important and fundamental result.
With a total energy E, S has many possible internal states (microstates). The atoms of S3 can share the total energy in many ways. Let's say there are N different states. Each state corresponds to a particular division of the total energy in the two subsystems S1 and S2. Many microstates can correspond to the same division, E1 in S1 and E2 in S2. A simple counting argument tells you that only one particular division of the energy, will occur with any significant probability. It's the one with the overwhelmingly largest number of microstates for the total system S3. That number, N(E1,E2) is just the product of the number of states allowed in each subsystem, N(E1,E2) = N1(E1)*N2(E2), and, since E1 + E2 = E, N(E1,E2) reaches a maximum when N1*N2 is stationary with respect to variations of E1 and E2 subject to the total energy constraint.
For convenience, physicists prefer to frame the question in terms of the logarithm of the number of microstates N, and call this the entropy, S. You can easily see from the above analysis that two systems are in equilibrium with one another when (dS/dE)1 = (dS/dE)2, i.e., the rate of change of entropy, S, per unit change in energy, E, must be the same for both systems. Otherwise, energy will tend to flow from one subsystem to another as S3 bounces randomly from one microstate to another, the total energy E3 being constant, as the combined system moves towards a state of maximal total entropy. We define the temperature, T, by 1/T = dS/dE, so that the equilibrium condition becomes the very simple T1 = T2.
This statistical mechanical definition of temperature does in fact correspond to your intuitive notion of temperature for most systems. So long as dS/dE is always positive, T is always positive. For common situations, like a collection of free particles, or particles in a harmonic oscillator potential, adding energy always increases the number of available microstates, increasingly faster with increasing total energy. So temperature increases with increasing energy, from zero, asymptotically approaching positive infinity as the energy increases.
Q15) What is "Negative Temperature"?
A15)
Not all systems have the property that the entropy increases monotonically with energy. In some cases, as energy is added to the system, the number of available microstates, or configurations, actually decreases for some range of energies. For example, imagine an ideal "spin-system", a set of N atoms with spin 1/2 on a one-dimensional wire. The atoms are not free to move from their positions on the wire. The only degree of freedom allowed to them is spin-flip: the spin of a given atom can point up or down. The total energy of the system, in a magnetic field of strength B, pointing down, is (N+ - N-)*uB, where u is the magnetic moment of each atom and N+ and N- are the number of atoms with spin up and down respectively. Notice that with this definition, E is zero when half of the spins are up and half are down. It is negative when the majority are down and positive when the majority are up.
The lowest possible energy state, all the spins pointing down, gives the system a total energy of -NuB, and temperature of absolute zero. There is only one configuration of the system at this energy, i.e., all the spins must point down. The entropy is the log of the number of microstates, so in this case is log(1) = 0. If we now add a quantum of energy, size uB, to the system, one spin is allowed to flip up. There are N possibilities, so the entropy is log(N). If we add another quantum of energy, there are a total of N(N-1)/2 allowable configurations with two spins up. The entropy is increasing quickly, and the temperature is rising as well.
However, for this system, the entropy does not go on increasing forever. There is a maximum energy, +NuB, with all spins up. At this maximal energy, there is again only one microstate, and the entropy is again zero. If we remove one quantum of energy from the system, we allow one spin down. At this energy there are N available microstates. The entropy goes on increasing as the energy is lowered. In fact the maximal entropy occurs for total energy zero, i.e., half of the spins up, half down.
So we have created a system where, as we add more and more energy, temperature starts off positive, approaches positive infinity as maximum entropy is approached, with half of all spins up. After that, the temperature becomes negative infinite, coming down in magnitude toward zero, but always negative, as the energy increases toward maximum. When the system has negative temperature, it is hotter than when it is has positive temperature. If you take two copies of the system, one with positive and one with negative temperature, and put them in thermal contact, heat will flow from the negative-temperature system into the positive-temperature system.
Q16) Enlist and explain any 2 molecular terms from Application of law of equi-partition energy in specific heat of a gas.
A16)
i) Monatomic molecule
Average kinetic energy of a molecule
=[ 3/2 kT]
Total energy of a mole of gas
= 3/2 kT × NA = 3/2 RT
For one mole, the molar specific heat at constant volume

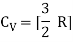

The ratio of specific heats,

Ii) Diatomic molecule
Average kinetic energy of a diatomic molecule at low temperature = 5/2kT
Total energy of one mole of gas
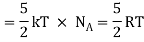
(Here, the total energy is purely kinetic)
For one mole Specific heat at constant volume

But 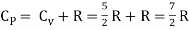
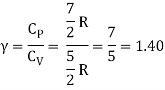
Energy of a diatomic molecule at high temperature is equal to 7/2RT
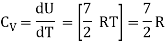
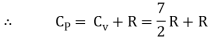
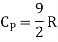
Note that the CV and CP are higher for diatomic molecules than the mono atomic molecules. It implies that to increase the temperature of diatomic gas molecules by 1°C it require more heat energy than monoatomic molecules.
Iii) Triatomic molecule
c) Linear molecule
Energy of one mole = 7/2 kT × NA = 7/2 RT
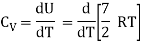

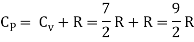
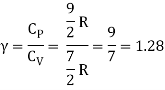
Q17) Define the Amounts of substance according to The Classical Entropy.
A17)
To express the behaviors of temperature and entropy quantitatively, we need to relate them with other physical quantities. Precisely, amounts of entropy happen to be essentially convertible into amounts of substance. Let us first explain what is this.
The amount of substance counts the very large number of atoms or molecules contained in macroscopic objects. Thus its deep meaning is that of natural numbers, but too big for the unit number (an individual atom or molecule) to be of any significance.
This concept comes from chemistry, as chemical reactions involve ingredients in precise proportions to form molecules containing the right numbers of atoms (this was first an observed fact at the beginning of the 19th century, until its explanation in terms of atoms was clearly established later that century).
The conventional unit for amounts of substance is the mol: 1 mol means NA molecules, where the number NA≈ 6.022×1023 is the Avogadro constant. Thus, n mol of some pure substance contains n×N A molecules of this substance.
This number comes from the choice that 1 mol of Carbon-12 weights 12 grams (thus roughly, 1 mol of hydrogen atoms weights 1 gram = 0.001 kg, with a slight difference due to the nuclear binding energy, converted into mass by E=mc2).
It can be seen as quantity NA ≈ 6.022×1023 mol-1.
Q18) Describe the Isentropic processes.
A18)
Any process in an open system which does not exchange heat with the environment is said to be adiabatic. If the process is furthermore reversible, it follows that ∂Q = 0 in each infinitesimal step, so that the ∂S = ∂Q/T = 0. The entropy must in other words stay constant in any reversible, adiabatic process. Such a process is for this reason called isentropic. By means of the adiabatic index we may write the entropy as,
S = CV log(TV γ−1) + const,(10)
From this it follows that
TV γ−1 = const,(11)
For any isentropic process in an ideal gas. Using the ideal gas law to eliminate V ∼ T/P, this may be written equivalently as,
TγP1−γ = const.(12)
Eliminating instead T ∼ PV , the isentropic condition takes its most common form,
PV γ = const.(13)
Q19) Define the two fundamental laws of thermodynamics.
A19)
The reason is that the two fundamental laws of thermodynamics are formulated in terms of the energy and the entropy. Both laws concern processes that may take place in an isolated system which is not allowed to exchange heat with or perform work on the environment. The First Law states that the energy is unchanged under any process in an isolated system. This implies that the energy of an open system can only change by exchange of heat or work with the environment. We actually used this law implicitly in deriving the heat capacities and the entropy. The Second Law states that the entropy cannot decrease. In the real world, the entropy of an isolated system must in fact grow. Only if all the processes taking place in the system are completely reversible at all times, will the entropy stay constant. Reversibility is an ideal which can only be approached by very slow quasistatic processes, consisting of infinitely many infinitesimal reversible steps. Essentially all real-world processes are irreversible to some degree.
Q20) What is Entropy?
A20)
When neither the volume nor the pressure are kept constant, the heat that must be added to the system in an infinitesimal process is,
δQ = ∂U + PδV = CV δ T + Nk T δV/V
It is a mathematical fact that there exists no function, Q(T,V ), which has this expression as differential. It may on the other hand be directly verified (by insertion) that
δS = δQ/T + CV δT/T + NK δV/V
Can be integrated to yield a function,
S = CV logT + Nk logV + c,
Called the entropy of the amount of ideal gas. Being an integral the entropy is only defined up to an arbitrary constant. The entropy of the gas is, like its energy, an abstract quantity which cannot be directly measured. But since both quantities depend on the measurable thermodynamic quantities that characterize the state of the gas, we can calculate the value of energy and entropy in any state.