Unit - 1
Coordination Chemistry
Q1) Explain Coordination compounds.
A1)
Coordination compounds are chemical compounds made up of an array of anions or neutral molecules bound together by coordinate covalent bonds to a central atom. Coordination complexes are another name for coordination compounds. The ligands are the molecules or ions that are bound to the central atom (also known as complexing agents).
Important Terms Involving Coordination Compounds
The meanings of some key words in coordination compound chemistry can be found below.
- Coordination Entity
A coordination object is a chemical compound in which the central ion or atom (or coordination centre) is bound to a certain number of atoms, molecules, or ions.
Some examples of such coordination entities include [CoCl3(NH3)3], and [Fe (CN)6]4-.
2. Central Atoms and Central Ions
The central atoms and ions, as previously mentioned, are the atoms and ions to which a certain number of atoms, molecules, or ions are bound.
The central atoms or ions in coordination compounds are usually Lewis Acids, which may serve as electron-pair acceptors.
3. Ligands
The ligands are the atoms, molecules, or ions that are bound to the coordination centre or the central atom/ion.
These ligands can be simple ions or molecules (like Cl– or NH3), or they can be relatively large molecules like ethane-1,2-diamine (NH2-CH2-CH2-NH2).
Coordination Number
The total number of sigma bonds by which the ligands are bound to the coordination centre is referred to as the coordination number of the central atom in the coordination compound.
Nickel, for example, has a coordination number of 4 in the coordination complex [Ni (NH3)4]2+.
● Coordination Sphere
The non-ionizable portion of a complex compound that is made up of a central transition metal ion surrounded by atoms or groups enclosed in square brackets.
When written together, the coordination sphere is formed by the coordination centre, the ligands attached to the coordination centre, and the net charge of the chemical compound as a whole.
A counter ion is normally present with this coordination sphere (the ionizable groups that attach to charged coordination complexes).
Example: [Co (NH3)6]C/3 – coordination sphere
● Coordination Polyhedron
The coordination polyhedron is the geometric shape created by the ligands' attachment to the coordination centre.
Tetrahedral and square planar spatial arrangements are examples of such spatial arrangements in coordination compounds.
● Oxidation Number
When all the electron pairs donated by the ligands are withdrawn from the central atom, the charge associated with it can be determined to determine its oxidation number.
For example, the oxidation number of the platinum atom in the complex [PtCl6]2- is +4.
● Homoleptic and Heteroleptic Complex
The coordination complex is called a homoleptic complex when the coordination centre is bound to just one kind of electron pair donating ligand group, for example: [Cu (CN)4]3- [Cu (CN)4]3- [Cu (CN)4]3-
2. The coordination compound in question is called a heteroleptic complex when the central atom is bound to several different forms of ligands, such as [Co (NH3)4Cl2] +.
● Properties of Coordination Compounds
This section discusses the general properties of coordination compounds.
1. The presence of unpaired electrons in the electronic transitions of the transition elements causes the coordination compounds produced by them to be coloured. Iron (II) complexes, for example, can be green or light green in colour, whereas coordination compounds containing iron (III) are brown or yellowish-brown in colour.
2. Because of the presence of unpaired electrons, the resulting coordination complexes have a magnetic nature when the coordination centre is a metal.
3. Coordination compounds are characterised by a wide range of chemical reactivity. They will take part in both inner-sphere and outer-sphere electron transfer reactions.
4. Complex compounds with specific ligands have the ability to catalyse or stoichiometrically help in the transformation of molecules.
Q2) What are Ligands in Coordination Compounds?
A2)
Ligands are the atoms, ions, and molecules that accompany the central transition metal ion. They serve as a Lewis base, donating electron pairs to the transition metal ion, forming a dative bond between the ligands and the transition metal ion. As a result, these compounds are known as coordination complexes.
● Types of Ligands
Based on the nature of the bond between the ligand and the central atom, ligands are classified as follows:
● Anionic ligands: CN–, Br–, Cl–
● Cationic ligands: NO+
● Neutral ligands: CO, H2O, NH3
Ligands can be further classified as:
● Unidentate Ligands
Unidentate ligands are ligands that only have one atom that can bind to the coordination centre. A good example of an unidentate ligand is ammonia (NH3). Cl–, H2O, and other unidentate are popular.
● Bidentate Ligands
Bidentate ligands, such as ethane-1,2-diamine, have the ability to bind to the central atom through two separate donor atoms.
The ion oxalate is a bidentate since it can bind to the central atom of a coordination compound through two atoms. Ethane-1, 2-diamine:
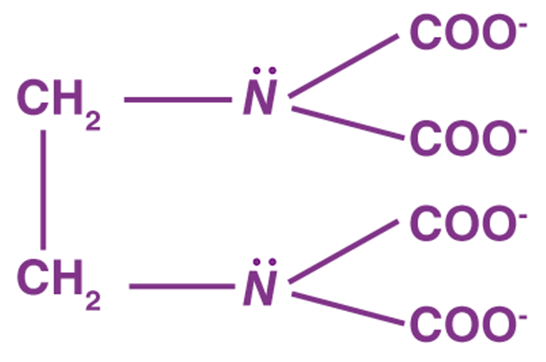
● Polydentate Ligands
Many donor atoms in some ligands may bind to the coordination centre. Polydentate ligands are the name given to these ligands.
The EDTA4- ion (ethylene diamine tetraacetate ion) is a polydentate ligand with four oxygen atoms and two nitrogen atoms that can bind to the coordination centre.
● Chelate Ligand
A chelate ligand is described as a polydentate ligand that binds to the same central metal atom through two or more donor atoms. The denticity of such ligands refers to the atoms that ligate to the metal ion.
● Ambidentate Ligand
Some ligands can bind to the central atom by using atoms from two separate elements.
The SCN– ion, for example, can bind to a ligand through the nitrogen or sulphur atoms. Ambidentate ligands are a type of ligand that has two ends.
Q3) Explain Werner’s theory.
A3)
Werner's theory, which explains the structure of coordination compounds, was introduced by Alfred Werner in 1898.
Werner's Experiment: All three chloride ions were converted to AgCl by combining AgNO3 (silver nitrate) with CoCl3•6NH3 (silver chloride). When AgNO3 was combined with CoCl3•5NH3, however, two moles of AgCl were formed.
In addition, one mole of AgCL was formed by mixing CoCl3•4NH3 with AgNO3. Based on this observation, Werner proposed the following theory:
● Postulates of Werner’s Theory
1 The coordination compound's central metal atom has two types of valencies: primary and secondary linkages or valencies.
2 Negative ions satisfy primary linkages, which are ionizable.
3 Secondary linkages cannot be ionised. Negative ions fulfil these needs. In addition, the secondary valence of any metal is set and equal to its coordination number.
4 The ions bound to the metal by secondary linkages have distinct spatial structures that correspond to different coordination numbers.
Q4) Difference between Primary and Secondary Valency in Coordination Compounds.
A4)
Werner’s Theory | |
Primary valency | Secondary valency |
These are ionizable | These are Non-ionizable |
Satisfied by charged ions | Satisfied by ligands |
Primary valency does not help in the structure of complex | Secondary valency helps in structure |
It can also function as a secondary valence | It cannot function as a primary valency |
Q5) Explain Valence bond theory.
A5)
VALENCE BOND THEORY - DEFINITION
A significant number of coordination compounds' structure and magnetic properties are explained by the valence bond theory. The structure of coordination compounds and the bond linkages were explained using the valence bond theory. According to valence bond theory, a metal atom or ion may use its (n-1)d, ns, np, nd orbitals for hybridization to yield a collection of identical orbitals of definite geometry such as octahedral, tetrahedral, square planar, and so on when it is influenced by ligands. The ligand orbitals that can donate electron pairs for bonding can overlap with the hybridised orbitals.
POSTULATES OF VALENCE BOND THEORY - DEFINITION
The valence-bond theory was based on the Heitler-London model of covalent bonds. Linus Pauling's suggestion that atomic orbitals mix to form hybrid orbitals, such as the sp, sp2, sp3, dsp3, and d2sp3 orbitals, was the final major step in the development of this theory.
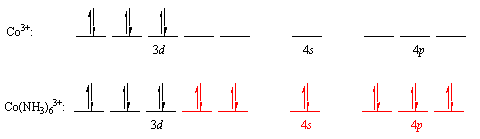
Some coordination complexes, such as the Co (NH3)63+ ion, are simple to apply the valence-bond principle to. The electron structure of the transition-metal ion Co3+ is first examined: [Ar]d6 is a character in the game [Ar]d6. The valence-shell orbitals are then examined, and the 4s and 4p orbitals are both empty. The following electron configuration is obtained by concentrating the 3d electrons in the dxy, dxz, and dyz orbitals in this subshell. The 3dx2y2,3dz2,4s,4px,4py, and 4pz orbitals are then combined to form a series of empty d2sp3 orbitals pointing toward the octahedron's corners. Both of these orbitals will accept a pair of non-bonding electrons from a neutral NH3molecule, resulting in a complex with a filled shell of valence electrons on the cobalt atom.
Q6) What are IUPAC nomenclature of coordination compounds.
A6)
Naming Transition Metals
Many transition metals come in a variety of cation types. Iron, for example, comes in two forms: Fe2+ and Fe3+. As a result, when naming an ionic compound containing iron, it is important to specify the metal's oxidation number. After the cation, the oxidation number appears as a Roman numeral in parenthesis. The oxidation number of metals is the same as the charge. Fe2+ in a chloride-containing compound has the formula FeCl2 and is known as iron(II) chloride. Iron(III) oxide is formed when the cation Fe3+ is combined with oxygen and has the formula Fe2O3.
The method for naming polyatomic ions-containing ionic compounds is the same as for simple ions. As a result, CaCO3 is known as calcium carbonate (NH4) Pb2+ combined with SO42- (PbSO4) is known as lead(II) sulphate, and 2HPO4, a compound with two polyatomic ions, is known as ammonium hydrogen phosphate.
1st example: For each of the following ionic compounds, write the proper chemical formula: Aluminium oxide, copper(II) chloride, and iron(III) oxide are all examples of oxides.
a. Aluminium is 3+, although oxide is 2-; Al2O3. b. Based on the oxidation state, copper is 2+ and chloride is 1-; CuCl2. c. The oxidation state of iron is 3+, while the oxide state is 2-; Fe2O3.
Example 2: For each of the following ionic compounds, write the proper chemical name: a. Li2S; b. NiCl2; c. FeO.
Solution 2: a. Since we aren't using multipliers, this is just lithium sulphide. b. Since nickel is 2+ in this compound, we must call it nickel(II) chloride. c. Since the iron in this compound is 2+, we must call it iron(II) oxide.
Naming Coordination Compounds
More complex coordination compounds are made up of an atom or ion (usually a metal) and a ligand-like sequence of bound molecules or anions. The donor atom is the atom in a ligand that is bound to the central atom or ion. Several donor atoms, which may be the same or different, are connected to a standard complex. The coordinate covalent bonds (dipolar bonds) between the ligands and the central atom are referred to as coordination.
The following are the principles for naming a teamwork compound:
- The ligands are numbered before the metal ion when naming a complex ion.
- List the ligands' names in the following order: neutral, negative, positive. If multiple ligands of the same charge form exist, they are called alphabetically. (Numerical prefixes have no impact on the ordering.)
- Monodentate ligands with several occurrences are given a prefix based on the number of occurrences: di-, tri-, tetra-, penta-, or hexa. Polydentate ligands (e.g., ethylenediamine, oxalate) obtain bis-, tris-, tetrakis-, and other forms of bis-, tris, tetrakis-, and other forms of bis-, tris-, tetrakis-, and other forms of bis-, tris-, te
- Anions end in the suffix -ido. This takes the place of the final "e" when the anion ends in "-ate" (e.g., sulphate becomes sulfato) and "-ide" when the anion ends in "-ide" (cyanide becomes cyanido).
- With a few exceptions, neutral ligands are assigned their normal names: NH3 becomes ammine, H2O becomes aqua or aquo, CO becomes carbonyl, and NO becomes nitrosyl.
- Write the central atom's or ion's name. The central atom's name will end in -ate if the complex is an anion, and its Latin name will be used if it is available (except for mercury).
- If the oxidation state of the central atom must be defined (it may be one of many or zero), write it in parentheses as a Roman numeral (or 0).
- Separate the words "cation" and "anion" at the end (if applicable).
Q7) What are Stereochemistry of complexes with 4 and 6 coordination numbers.
A7)
Geometrical isomerism in complexes with coordination number 4
I Geometrical isomerism does not exist in tetrahedral complexes.
(ii) Geometrical isomerism is observed in square planar complexes of the formula [MX2L2] (where X and L are unidentate). In a cis isomer, the two X ligands may be located next to each other, while in a trans isomer, they may be arranged opposite each other, as in,
(iii) The [MABXL] square planar complex (where A, B, X, L are unidentate ligands) has three isomers, two cis and one trans.
e.g., [Pt(NH3) (Br)(Cl)(Py)].
Geometrical isomerism in complexes with coordination number 6
[Co(NH3)4Cl2)+ is an octahedral complex with the formula [MX2L4], in which the two X ligands can be directed cis or trans to each other.
[MX2A2] Octahedral complexes, where X denotes unidentate ligands and A denotes bidentate ligands. [CoC12(en)2]
If three donor atoms of the same ligands occupy adjacent positions at the corners of an octahedral face in octahedral complexes of formula [MA3X3]. It is known as facial (fae) isomer when the positions are near the octahedron's meridian, and it is known as meridional (mer) isomer when the positions are around the octahedron's meridian. [Co(NH3)3(NO2)3] is an example.
(ii) Optical isomerism: The chiral complexes are those that have chiral structures. When mirror images can't be superimposed on top of each other, this problem occurs. Enantiomers are mirror images of each other. The two forms are known as dextro (d) and laevo (l).
Optical isomerism can be seen in tetrahedral complexes with the formula [M(AB)2] and octahedral complexes (cis form).
Q8) Explain Labile and inert complexes.
A8)
The ease with which ligands can be substituted in coordination complexes is referred to as lability. In the following example, Scandium is referred to as "labile."
[Sc(OH2)6] [Sc(OH2)6] [Sc(OH2)6
6 NaSCN + Cl3 —> Na3
3 NaCl + [Sc(SCN)6] (quick!)
The term lability refers to the ease with which metal-ligand bonds can be broken. The term "labile" refers to a compound in which the metal-ligand bonds are easily broken. The term "inert" refers to a compound in which the metal-ligand bonds are more difficult to break.
By comparing the factors that control bond strengths in ionic complexes to observations about the rates of reaction of coordination complexes, Henry Taube (Nobel Prize, 1983) attempted to understand lability. He noticed some unsurprising incidents. He also came up with some new ligand field theory conclusions.
Many M+1 ions (M = metal) are more labile than many M+3 ions, according to Taube. In forming coordination complexes, metal ions act as electrophiles or Lewis acids, and ligands act as nucleophiles or Lewis bases, which isn't shocking. In other words, higher-charged metals should be stronger Lewis acids and therefore bind ligands more tightly.
There were, however, exceptions to the general rule. Taube discovered that Mo(V) compounds are more labile than Mo(III) compounds, for example. That implies that there's more going on here than charge effects.
The size of the ion is another aspect that influences the strength of ionic bonds. Ions with smaller atomic radii, on average, form stronger bonds than ions with larger radii. The ions Al3+, V3+, Fe3+, and Ga3+ are all around the same scale, according to Taube. These ions all exchange ligands at a similar rate. Since they have the same charge and radius, this isn't shocking.
Cr3+, on the other hand, is around the same size as those ions and has the same charge, but it is much less labile. Again, due to basic electrostatic considerations, there are exceptions to our usual expectations.
Furthermore, transition metals in the second and third rows (Y-Cd and Ac-Hg) are much more inert than those in the first row (Sc-Zn). That's a little odd, given how much larger the lower metals are than the first row metals.
It does, however, provide insight into other factors that influence lability. Second- and third-row metals have much higher d orbital splitting energies than first-row metals, according to ligand field theory. This is often described in terms of larger atoms' diffuse orbitals forming stronger bonds with ligands, reminding us that we're not only concerned with electrostatic interactions.
Taube wondered if the electron configuration of a compound affected whether it was labile or inert. Taube's lability rules are based on this concept.
Metals like Ni2+ and Cu2+, for example, are extremely labile. For those substances, the d orbital splitting diagrams will have d electrons in the eg set. Remember that the eg set is formed by interactions with the ligand donor orbitals, and it corresponds to an antibonding degree.
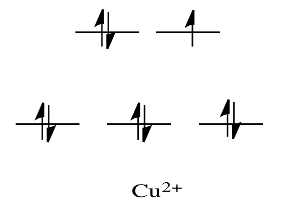
By comparison, V2+ is rather inert. The d orbital splitting diagram in this case has electrons in the t2g set, but none in the eg set.
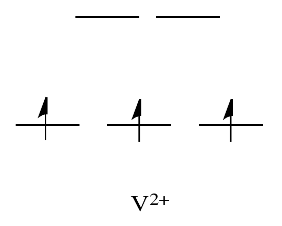
As a result, having electrons at a higher energy level weakens the bond between the ligand and the antibonding eg level, allowing the ligand to be replaced more easily. The bond to the ligand is stronger in the absence of those higher energy electrons, and the ligand isn't as easily replaced.
Metals like Ca2+, Sc3+, and Ti4+, on the other hand, are rather labile. In such cases, the d orbital splitting diagrams are straightforward: the ions have no d electrons at all.
Since these mainly non-bonding levels have no electrons, the complex is vulnerable to ligand replacement. However, it's difficult to see how the population of a non-bonding orbital will affect ligand bond power.
Instead, this element is most likely related to the aspect of ligand substitution that we have so far overlooked. Not only must one ligand depart, but another must also bond in its position. Having an empty orbital for the ligand to donate electrons into (or, to put it another way, not having electrons in the way that would confuse ligand donation) simplifies that part of the reaction
Q9) What is Crystal field theory?
A9)
The net change in crystal energy caused by the orientation of d orbitals of a transition metal cation within a coordinating group of anions, also known as ligands, is defined by crystal field theory.
Transition metals are known for their proclivity for forming complexes. A complex is made up of a central metal atom or ion that is surrounded by a variety of ligands. Crystal field theory governs the interaction of these ligands with the central metal atom or ion.
The interaction of a metal ion and a ligand is treated as a strictly electrostatic phenomenon in crystal field theory, which considers the ligands as point charges in the vicinity of the central atom's atomic orbitals. The partly covalent existence of bonds between the ligand and metal atom was taken into account in the development and extension of crystal field theory, primarily through the use of molecular orbital theory. Ligand field theory is another name for crystal field theory.
Overview of Crystal Field Theory
Awareness of the geometrical or spatial disposition of d orbitals is needed to clearly understand crystal field interactions in transition metal complexes. In a free gaseous metal ion, the d-orbitals are fivefold degenerate. When a spherically symmetric area of negative ligand filed charge is applied to a central metal ion, the d-orbitals remain degenerate, but the energy of the free ion changes.
The relationships are summarised in the table below.

Crystal Field Splitting
The metal-ligand bond was defined as an ionic bond arising solely from electrostatic interactions between metal ions and ligands in the crystal field theory. Anions are treated as point charges in crystal field theory, while neutral molecules are treated as dipoles.
Transition metals' d orbitals are degenerate, meaning they have the same energy when they are not bound to any ligand. As they start bonding with other ligands, the d orbitals break apart and become non-degenerate due to different symmetries of the d orbitals and the inductive effect of the ligands on the electrons.
High Spin and Low Spin
The high spin complex is the complexion with the most unpaired electrons, while the low spin complex has the least number of unpaired electrons. With weak field ligands, high spin complexes are required because the crystal field splitting energy is low. Low spin complexes, on the other hand, have strong field ligands that induce maximum electron pairing in the collection of three t2 atomic orbitals due to large o.
● High spin – Maximum number of unpaired electrons.
● Low spin – Minimum number of unpaired electrons.
Q10) Definition: Crystal field stabilization energy.
A10)
Stabilization of the Crystal Field The energy of the electron configuration in the ligand field is subtracted from the energy of the electronic configuration in the isotropic field to get energy.
CFSE=E=Eligand field Eisotropic
The CSFE will be determined by a number of factors, including:
- Geometry is the study of the shape of things (which changes the d-orbital splitting patterns)
- The number of d-electrons is the number of electrons in a molecule.
- Energy of Spin Pairing
- Character of ligand (via Spectrochemical Series)
- An electron in the more stable t2g subset contributes 2/5o to an octahedral complex, while an electron in the higher energy eg subset contributes +3/5o to destabilisation. After that, the result is expressed as a multiple of the crystal field splitting parameter o. The term PP is used to describe the spin pairing energy when any electrons are paired within a single orbital.
Q11) Definition: Octahedral site preference energy.
A11)
The difference between the CFSE energies of a non-octahedral complex and the octahedral complex is known as the Octahedral Site Preference Energy (OSPE). The OSPE is OSPE=CFSE(oct)CFSE(tet) for comparing the preference for forming an octahedral ligand field vs. a tetrahedral ligand field (2)
The OSPE is a measurement of a complex's preference for octahedral over tetrahedral geometry.
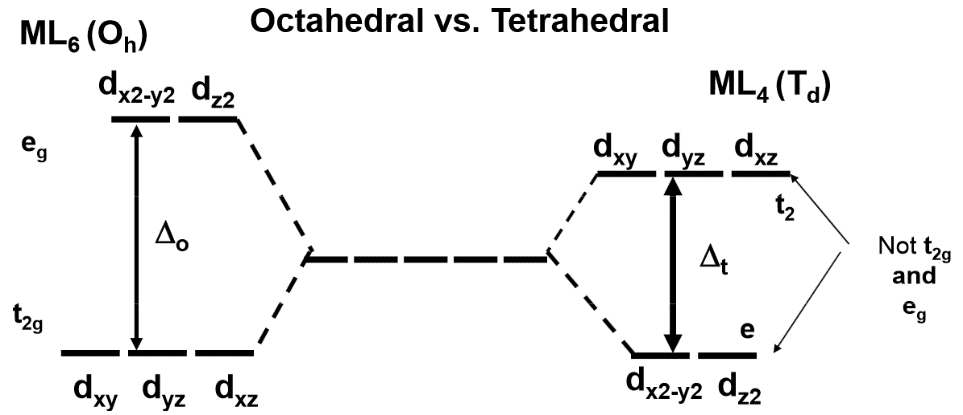
Note: the conversion between Δo and Δt used for these calculations is:
Δt≈49Δo(3)
Which is applicable for comparing octahedral and tetrahedral complexes that involve same ligands only.
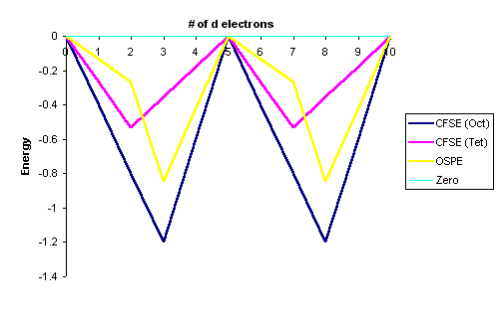
Table: Octahedral Site Preference Energies (OSPE) | |||||
Total d-electrons | CFSE(Octahedral) | CFSE(Tetrahedral) | OSPE (for high spin complexes)** | ||
| High Spin | Low Spin | Configuration | Always High Spin* |
|
d0 | 0 ΔoΔo | 0 ΔoΔo | e0 | 0 ΔtΔt | 0 ΔoΔo |
d1 | -2/5 ΔoΔo | -2/5 ΔoΔo | e1 | -3/5 ΔtΔt | -6/45 ΔoΔo |
d2 | -4/5 ΔoΔo | -4/5 ΔoΔo | e2 | -6/5 ΔtΔt | -12/45 ΔoΔo |
d3 | -6/5 ΔoΔo | -6/5 ΔoΔo | e2t21 | -4/5 ΔtΔt | -38/45 ΔoΔo |
d4 | -3/5 ΔoΔo | -8/5 ΔoΔo + P | e2t22 | -2/5 ΔtΔt | -19/45 ΔoΔo |
d5 | 0 ΔoΔo | -10/5 ΔoΔo + 2P | e2t23 | 0 ΔtΔt | 0 ΔoΔo |
d6 | -2/5 ΔoΔo | -12/5 ΔoΔo + P | e3t23 | -3/5 ΔtΔt | -6/45 ΔoΔo |
d7 | -4/5 ΔoΔo | -9/5 ΔoΔo + P | e4t23 | -6/5 ΔtΔt | -12/45 ΔoΔo |
d8 | -6/5 ΔoΔo | -6/5 ΔoΔo | e4t24 | -4/5 ΔtΔt | -38/45 ΔoΔo |
d9 | -3/5 ΔoΔo | -3/5 ΔoΔo | e4t25 | -2/5 ΔtΔt | -19/45 ΔoΔo |
d10 | 0 | 0 | e4t26 | 0 ΔtΔt | 0 ΔoΔo |
The spin pairing energy, or PP, is the amount of energy needed to pair electrons in the same orbital.
Since the splitting in tetrahedral complexes is much smaller than in PP, they are still high spin (Equation).
Equation was used to convert the data. The curves in Figure 11 below graphically show the data in Tables for the high spin complexes only. The graphing of low spin complexes necessitates PP information.
Q12) State Jahn-Teller theorem.
A12)
In terms of its electronic state, Hermann Jahn and Edward Teller proposed a theorem in 1937 stating that "stability and degeneracy are not possible simultaneously unless the molecule is a linear one." This causes a degeneracy break, which stabilises the molecule and, as a result, decreases its symmetry. Since 1937, the theorem has been revised to "any non-linear molecular system in a degenerate electronic state will be unstable and will undergo distortion to form a system of lower symmetry and lower energy, thus eliminating the degeneracy," as Housecroft and Sharpe put it. This occurs most often in transition metal octahedral complexes, but it can also occur in tetrahedral compounds.
When constructing a molecular orbital diagram for a given octahedral complex, the five d atomic orbitals are split into two degenerate groups. The symmetry codes for these sets are t2g (dxz, dyz, dxy) and eg (dz2 and dx2y2). When a molecule's electronic ground state is degenerate, it can distort to eliminate the degeneracy and form a lower energy (and, as a result, lower symmetry) system. As shown in Figure 1, the octahedral complex can either elongate or compress the z ligand bonds:
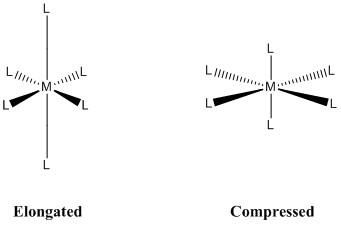
Figure: Jahn-Teller distortions for an octahedral complex.
The axial bonds of an octahedral complex are longer than the equatorial bonds as it experiences elongation. In the case of compression, the equatorial bonds are longer than the axial bonds. The amount of overlap between the metal and ligand orbitals determines the elongation and compression effects. As a result, the distortion varies greatly depending on the metal and ligands used. In general, the stronger the metal-ligand orbital interactions are, the more likely a Jahn-Teller effect may appear.
Q13) Explain Electronic configuration.
A13)
In transition metals, degeneracy in either the t2g or eg orbitals is needed for Jahn-Teller effects to occur. The number of d-electrons and the splitting energy determine the electronic states of octahedral complexes. Electrons pair in t2g before occupying eg when is large and greater than the energy needed to pair electrons. When Delta is small and less than the pairing energy, however, electrons will occupy eg before pairing in t2g. The chemical environment (ligand identification) and the identity and charge of the metal ion determine the of an octahedral complex. If the number of paired electrons in a given d-electron count varies, the configuration with the most paired electrons is called low spin, while the one with the most unpaired electrons is called high spin.
The figures below show electron configuration diagrams for d1 through d10 with large and small electrons. No matter what the magnitude of, the electron configurations for d1, d2, d3, d8, d9, and d10 are the same. Only the electron counts d4, d5, d6, and d7 have low and high spin configurations.
● Large Δ
Figure (below) shows the various electronic configurations for octahedral complexes with large ΔΔ, including the low-spin configurations of d4, d5, d6, and d7:
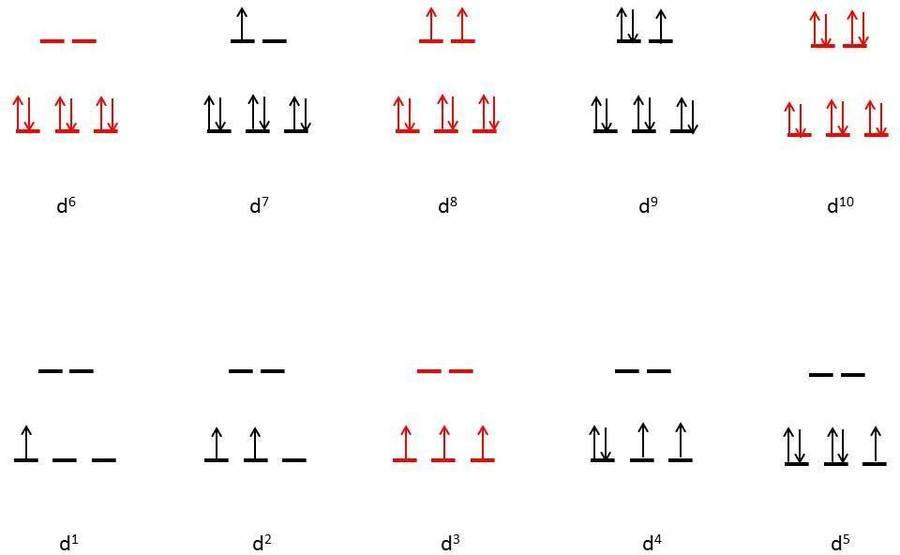
Figure: Octahedral dynamic electron structure diagram (red indicates no degeneracies possible, thus no Jahn-Teller effects).
The electron configurations in the case of large are depicted in the diagram. There are no Jahn-Teller distortions in the electron configurations illustrated in red (d3, low spin d6, d8, and d10). On the other hand, Jhan-Teller distortion is predicted in d1, d2, low spin d4, low spin d5, low spin d7, and d9. Transition metals are represented by these electronic configurations. Cr3+, Co3+, and Ni2+ are only a few examples.
Small Δ
Figure (below) shows the various electronic configurations for octahedral complexes with small Δ, including the high-spin configurations of d4, d5, d6, and d7:
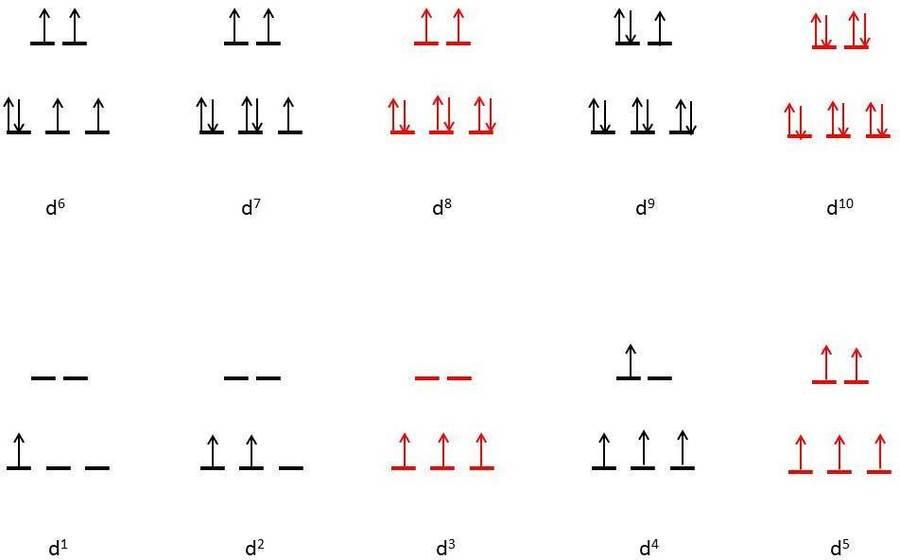
Q14) Explain Square planar geometry.
A14)
Square planar geometry is another famous geometry. A square planar geometry can be modelled as an octahedral structure with a pair of trans ligands removed. The ligands that have been removed are thought to be on the z-axis. This alters the d orbital distribution, making orbitals on or near the z-axis more stable while orbitals on or near the x- or y-axes become less stable. The octahedral t2g and eg sets break as a result, resulting in a more complicated splitting pattern.
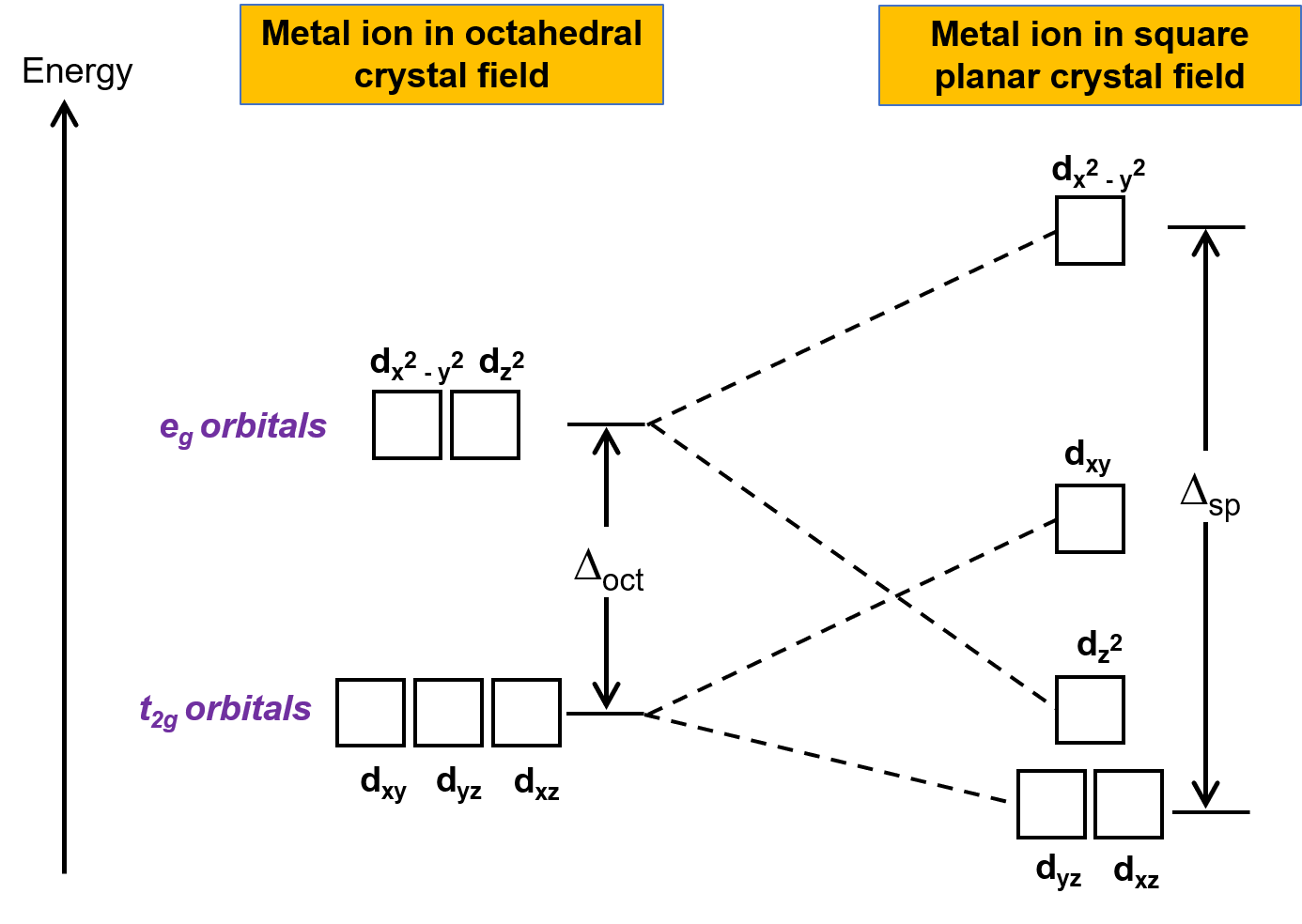
Figure. In a square planar crystal region, the t2g set and the eg set of orbitals are split. Square planar complexes, or sp, have a higher crystal field splitting energy than oct.
In another way:
A central atom is surrounded by constituent atoms that form the corners of a square on the same plane in square planar molecular geometry. Transition metal complexes with a d8 configuration are prone to this geometry. Rh(I), Ir(I), Pd(II), Pt(II), and Au are examples of this (III). Cisplatin (PtCl2(NH3)2) and other anticancer drugs are notable examples.
The coordination number of a square planar complex is also four. The ligands form a simple square on the x and y axes, which distinguishes the complex from a tetrahedral structure. The crystal field splitting is also different as a result of this (Figure 1). The repulsion of electrons in the dxz, dyz, and dz2 orbitals is significantly lower in a square planar complex than in an octahedral complex since there are no ligands along the z-axis (the dz2dz2 orbital is slightly higher in energy to the "doughnut" that lies on the x,y axis). The most energy is in the dx2y2 orbital, which is followed by the dxy orbital, which is followed by the remaining orbtails (although dz2 has slightly more energy than the dxz and dyz orbital). Throughout all geometries, this pattern of orbital splitting remains constant. Orbitals that come into direct contact with the ligand fields have higher energies than orbitals that slide past the ligand field and have more indirect contact. So, if you're not sure which geometry leads to which splitting, consider how the ligand fields interact with the central atom's electron orbitals.
Q15) Write a note on Ligand field theory.
A15)
Ligand Field Theory can be thought of as an extension of Crystal Field Theory in that it can account for all levels of covalent interactions. In certain cases, Molecular Orbital Theory is used to treat bonding in LFT. The following three diagrams show a qualitative approach that can be used for octahedral metal complexes.
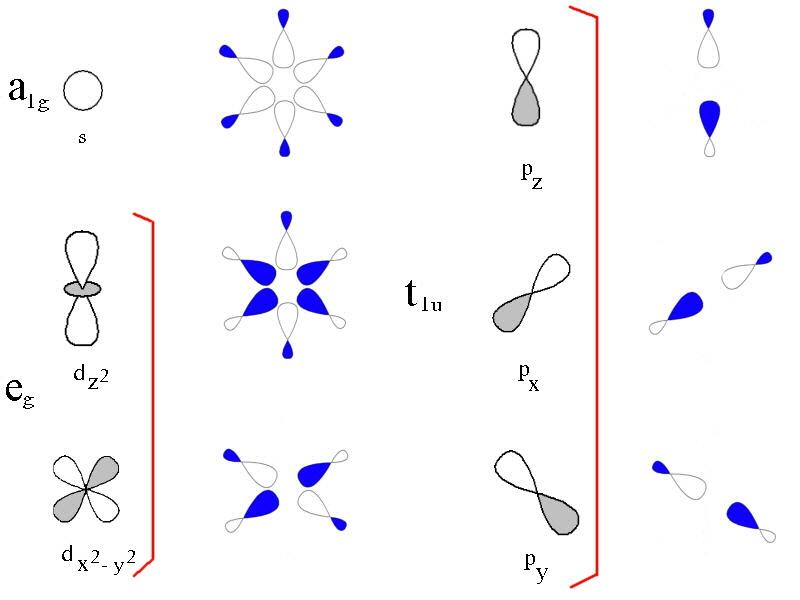
The 3d, 4s, and 4p metal ion atomic orbitals are seen in the first diagram, along with the ligand group orbitals that would have the right symmetry to overlap with them. The symmetry adapted linear combination of ligand orbitals is created by combining 6 sigma orbitals from the ligands designated as x, -x, y, -y, z, -z to form 6 ligand group orbitals.
(Labelled eg, a1g, t1u)

Only sigma bonding is seen in the second diagram, which depicts the combination of metal 3d, 4s, and 4p orbitals with OCCUPIED ligand group orbitals (using 1 orbital from each ligand). The metal electrons will then be fed into the t2g and eg* molecular orbitals, similar to the CFT model except that the eg orbital is now eg*.
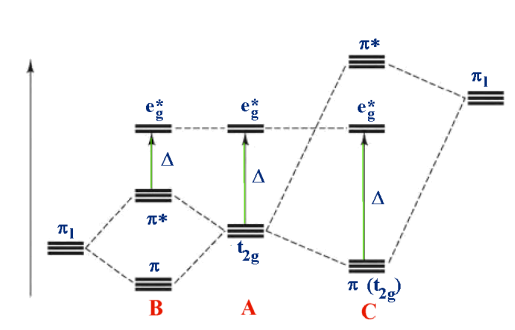
Consider the following scenario: [M(II)I6] - [M(II)I6] - [M(II)I6] 4- A - [M(II)(H2O)6] [M(II)(H2O)6] [M(II)(H2O) [M(II)(CN)6] 2+ C 4- (pi) bonding is considered in the third diagram. Bonds are weaker in general than (sigma) bonds, so the effect is to adjust rather than drastically change the definition. Two orbitals from each ligand are added together to make a total of 12, which is then split into four groups, each with three ligand group orbitals. These are designated by the letters t1g, t1u, t2g, and t2u. In both of the cases above, the metal t2g orbital is the most suitable for interaction.
Q16) What is Molecular Orbital Theory?
A16)
The Molecular Orbital Theory (often abbreviated to MOT) is a chemical bonding theory formulated by F. Hund and R. S. Mulliken at the turn of the twentieth century to explain the structure and properties of various molecules. The valence-bond theory failed to sufficiently understand how many molecules, such as resonance-stabilized molecules, contain two or more identical bonds whose bond orders lie between those of a single bond and those of a double bond. The molecular orbital theory was found to be more strong than the valence-bond theory in this case (since the orbitals described by the MOT reflect the geometries of the molecules to which it is applied).
The molecular orbital theory's main features are described below.
The total number of molecular orbitals produced equals the total number of atomic orbitals given by the bonding species.
Bonding molecular orbitals, anti-bonding molecular orbitals, and non-bonding molecular orbitals are the three types of molecular orbitals. Anti-bonding molecular orbitals will always have more energy than the parent orbitals, while bonding molecular orbitals will always have less energy.
In order of increasing orbital energy, electrons are filled into molecular orbitals (from the orbital with the lowest energy to the orbital with the highest energy).
When the combining atomic orbitals have identical energies, the most powerful combinations of atomic orbitals (for the creation of molecular orbitals) occur.
The molecular orbital theory notes, in simple terms, that each atom appears to combine and form molecular orbitals. Electrons are present in various atomic orbitals as a result of this arrangement, and they are normally associated with different nuclei. In a molecule, an electron can be found anywhere in the molecule.
One of the most significant effects of the molecular orbital theory since its formulation was that it opened up new avenues for understanding the bonding mechanism. According to this theory, molecular orbitals are essentially linear combinations of atomic orbitals. The Schrödinger equation is further approximated using the Hartree–Fock (HF) or density functional theory (DFT) models
The molecular orbitals can be approximated as linear combinations of atomic orbitals using the molecular orbital theory.
However, in order to comprehend the molecular orbital theory more simply and thoroughly, it is necessary to first comprehend what atomic and molecular orbitals
Q17) Explain characteristics of Bonding Molecular Orbitals.
A17)
● The chance of having the electron in the bonding molecular orbital's internuclear region is higher than that of mixing atomic orbitals.
● The attraction between the two atoms is caused by the electrons in the bonding molecular orbital.
● As a consequence of attraction, the bonding molecular orbital has a lower energy and thus is more stable than the combining atomic orbitals.
● They are generated by the additive effect of the atomic orbitals, with the new wave's amplitude equal to = A + B.
● They are represented by the letters.
Q18) Explain characteristics of Anti - Bonding Molecular Orbitals.
A18)
● In the anti-bonding molecular orbitals, the chance of having the electron in the internuclear field decreases.
● The electrons in the anti-bonding molecular orbital cause the two atoms to repel one another.
● Because of the repulsive forces, the anti-bonding molecular orbitals have a higher energy and are less stable.
● They are created by the atomic orbitals' subtractive effect. The new wave's amplitude is given by the formula = A – B.
● They are represented by
Q19) Difference between Bonding and Antibonding Molecular Orbitals.
A19)
Bonding Molecular Orbitals | Anti-Bonding Molecular Orbitals |
Bonding molecular orbitals are molecular orbitals created by the additive effect of atomic orbitals. | Anti-bonding molecular orbitals are created by the subtractive effect of atomic orbitals. |
In the case of bonding molecular orbitals, the probability of finding electrons is higher. | Antibonding molecular orbitals have a lower probability of finding electrons. There is also a node where the electron density is zero between the anti-bonding molecular orbitals of two nuclei. |
These are made up of a mixture of + and + as well as – of – electron waves. | The intersection of the + and – parts create these. |
In the internuclear field, the electron density in the bonding molecular orbital is strong. As a result, the nuclei are protected from each other, and repulsion is reduced significantly. | In the internuclear field, the electron density in the antibonding molecular orbital is very low, so the nuclei are directly exposed to each other. As a result, the nuclei are less protected from one another. |
The bonding molecular orbitals are denoted by | The anti-bonding molecular orbitals corresponding to the corresponding anti-bonding molecular orbitals are described by σ∗, π∗, δ∗. |
Q20) Define features of Molecular Orbital Theory.
A20)
● The atomic orbitals collide to form molecular orbitals, which are new orbitals. When two atomic orbitals collide, their identities are lost and new orbitals called molecular orbitals are formed.
● The electrons in molecules are filled in new energy states called Molecular orbitals, similar to how electrons in an atom are filled in atomic orbitals. The molecular orbital determines the likelihood of having the electronic distribution in a molecule around its group of nuclei.
● The two merging atomic orbitals should have identical energies and a similar orientation. 1s, for example, can be combined with other 1s but not with 2s.
● The number of atomic orbitals combining equals the number of molecular orbitals produced.
● The shape of the combining atomic orbitals determines the shape of the molecular orbitals produced.
According to the Molecular Orbital Theory, the filling of orbitals takes place according to the following rules:
● Molecular orbitals are filled in increasing order of energy levels, according to the Aufbau theory.
● Pauli's exclusion theory states that no two electrons in an atom or molecule can have the same set of four quantum numbers.
● Hund's maximum multiplicity rule: Electron pairing does not occur until all atomic or molecular orbitals are singly occupied.