Unit - 1
Conductance-I
Q1) Explain Arrhenius theory of electrolytic dissociation.
A1) When dissolved in water, an electrolyte separates into two types of charged particles, one with a positive charge and the other with a negative charge. Ions are charged particles with a positive charge. Cations are positively charged ions, while anions are negatively charged.
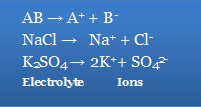
The contemporary version of the idea states that solid electrolytes are made up of ions kept together by electrostatic attraction. These forces are diminished when an electrolyte is dissolved in a solvent, and the electrolyte dissociates into ions. The ions have been solvated.
Ionization is the process of breaking down molecules into ions in an electrolyte. The degree of ionisation or degree of dissociation is the percentage of total molecules present in solution that are ions. It's indicated by
It has been discovered that not all electrolytes ionise to the same degree.
Some are nearly totally ionised, whereas others are only marginally ionised. A lot of things influence the degree of ionisation.
Ions in solution constantly re-unite to produce neutral molecules, resulting in a condition of dynamic equilibrium between the ionised and non-ionized molecules, i.e., AB A+ + B-.
Applying the law of mass action to situations that aren't in equilibrium =K [A+] [B-] /[AB]
The ionisation constant is K. Electrolytes with a high K value are known as strong electrolytes, whereas those with a low K value are known as weak electrolytes.
Electrolysis happens when an electric current is passed through an electrolytic solution and the positive ions (cations) travel towards the cathode and the negative ions (anions) travel towards the anode and are discharged.
Ions are always discharged in equal amounts, regardless of their relative speeds.
The total charge on one set of ions is always equal to the total charge on the other set of ions, making electrolytic solutions always neutral. However, the number of ions in two sets does not have to be equal all of the time.
AB  | NaCl 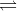 | (Both ions are equal) |
AB2 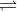 | BaCl2  | (Anions are double that of cations) |
A2B 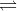 | Na2SO4 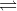 | (Anions are double that of cations) |
Electrolytes in solution have properties that are similar to those of ions in solution. For example, acidic solutions always contain H+ ions, whereas basic solutions contain OH- ions, and the characteristics of H- ions and OH- ions are the same in both cases.
The ions act as molecules to lower the freezing point, raise the boiling point, lower the vapour pressure, and establish the osmotic pressure. The conductiveness of an electrolytic solution is determined by the nature and number of ions because current is carried through the solution by ion movement.
Q2) Explain Ohm’s Law Applicability.
A2) Electrolytic solutions, like metallic conductors, follow Ohm's law, which states that the current flowing conductor's strength is proportional to the potential difference (E) applied across the conductor and inversely proportional to the conductor's resistance. I = E/R is a mathematical formula.
Only if ions are already present in the solution and no part of the current has a direct influence on the ions is this possible.
Q3) Explain Ionic Reaction.
A3) Well-known inorganic chemistry processes provide evidence for the presence of ions in aqueous electrolyte solutions. When Ag+ ions come into contact with chloride ions, a white precipitate of silver chloride forms.
When AgNO3 solution is introduced to CCl4, CHCl3, or C2H5Cl, however, no precipitation occurs because these compounds are non-electrolytes and do not provide Cl- ions in solution.
Because no ionisation of the acid happens in the common reaction, an acid that gives all tests of H+ ions in aqueous solution does not give the same tests when dissolved in any organic solvent.

Q4) Explain Heat of Neutralization.
A4) The heat released when one gramme equivalent of a strong acid is neutralised by one gramme equivalent of a strong base is always the same, i.e., 13.7 kcal. This can be explained using the Arrhenius hypothesis, which states that when an acid is dissolved in water, it produces H+ ions and OH- ions, and the neutralisation process involves the common reaction.
13.7 kcal = H+ + OH- H2O
As a result, the heat of neutralisation is the heat of forming H2O from H+ and OH- ions.
Q5) Give Limitations of Arrhenius Theory.
A5) Strong electrolytes do not obey Ostwald's dilution law, which is based on Arrhenius theory, because they conduct electricity in their infused condition, that is, in the absence of water. This is in contrast to Arrhenius theory, which states that ionisation requires the presence of a solvent. Arrhenius theory assumes independent existence of ions but fails to account for the factors that govern ion mobility.
Factors Pertaining to Degree of Ionization
The degree of ionization of an electrolyte in solution depends upon the following factors:
● Nature of Solute
Less ions are produced in solution when the ionisable sections of a substance's molecule are bound together by covalent bonding rather than electrovalent bonding. Weak electrolytes are the name given to such compounds. This group includes H2S, HCN, NH4OH, and CH3COOH. Strong electrolytes such as NaCl, Ba(NO3)2, KOH, and others, in which electron transport appears to be more or less complete, produce ions almost instantly when dissolved. In solution, strong electrolytes are practically totally ionised.
● Nature of Solvent
The solvent's principal job is to break up the electrostatic interaction between the two ions and separate them. In any medium, the force of attraction that holds the ions together is expressed as
F= 1/ (K) (q1 q2)/r2
Where K is the dielectric constant of medium.
Any solvent with a high dielectric constant value has the ability to separate ions. Because it has the highest dielectric constant, water is thought to be the best solvent. At 250°C, the dielectric constants of some of the solvents are listed below.
Solvent | Dielectric Constant |
Water | 81 |
Methyl alcohol | 35 |
Ethyl alcohol | 27 |
Acetone | 21 |
● Dilution
The concentration of an electrolyte's solution is inversely related to the level of ionisation. When a result, as the dilution of the solution grows, the degree of ionisation increases, implying that the concentration of the solution decreases.
● Temperature
The degree of ionisation increases as the temperature rises. This is because when the temperature rises, the molecular speed increases, overcoming the forces of attraction between the ions.
Q6) Give Variation of molar conductivity with concentration.
A6) The ability to conduct molar water
The conductance of volume V of a solution containing one mole of electrolyte retained between two electrodes with an area of cross-section A and a distance of unit length is the molar conductivity of a solution at a particular concentration.
K/c = m
In this case,
c = moles per volume concentration
a measure of a substance's ability to conduct electricity.
Molar conductivity is denoted by the letter m.
Because there is just one mole of electrolyte in the solution, the previous equation can be changed to:
V = m
As the total volume, V, of a solution containing one mole of electrolyte grows, molar conductivity increases with decreasing concentration. The concentration drops as a result of dilution. The molar conductivity of a solution is known as limiting molar conductivity, °m, when the concentration approaches zero. Strong and weak electrolytes have different molar conductivity variations with concentration.

For strong electrolytes, molar conductivity varies with concentration:
The molar conductivity of strong electrolytes increases slowly with dilution. The plot of molar conductivity vs c1/2 is a straight line with a y-intercept of °m. The value of the limiting molar conductivity, °m, can be calculated using either the graph or the Kohlrausch law. The plot's general equation is as follows:
The molar conductivity of strong electrolytes increases slowly with dilution. The plot of molar conductivity vs c1/2 is a straight line with a y-intercept of °m. The value of the limiting molar conductivity, °m, can be calculated using either the graph or the Kohlrausch law. The plot's general equation is as follows:
m = °m -Ac1/2 m = °m -Ac1/2 m = °m -Ac1/2
Where -A is the slope of the line as a constant. The value of "A" for a given solvent is determined by the type of electrolyte present at a specific temperature.
With a poor electrolyte concentration:
The graph between molar conductivity and c1/2 (where c is the concentration) is not a straight line for weak electrolytes. At greater concentrations, weak electrolytes have lower molar conductivities and a lower degree of dissociation, which increases quickly at lower concentrations. As a result, by extrapolating molar conductivity to zero concentration, m° cannot be achieved as a limiting molar conductivity. As a result, we apply the Kohlrausch law of independent ion migration to determine the molar conductivity, m°, of weak electrolytes.
Q7) Explain Weak and Strong Electrolytes.
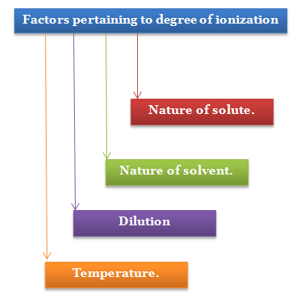
A7) The systematic research of electrolytic solutions began in the late 1800s, mostly in Germany, before the specifics of dissociation and ionisation were well understood. These experiments discovered that the equivalent conductivities of electrolytes all decrease with concentration (or, more precisely, with the square root of the concentration), but in different ways, as seen by their behaviour at very low concentrations. As a result, electrolytes were divided into three categories: weak, intermediate, and strong.
You'll note that conductivities vs. c graphs begin at c=0. Of course, measuring the conductance of an electrolyte at vanishingly small concentrations (let alone 0!) is impossible, but for strong and intermediate electrolytes, a sequence of observations can be extrapolated to zero. The resulting values, denoted by °, are known as limiting equivalent conductance’s or "equivalent conductance’s at infinite dilution."
Strong electrolytes
Intermediate electrolytes
Weak electrolytes
Q8) What are Molar conductivity at infinite dilution?
A8) Limiting molar conductivity is the molar conductivity of a solution at infinite dilution. In other words, the molar conductivity is known as limiting molar conductivity as the electrolyte concentration approaches zero.
Conductivity drops as the number of ions per unit volume that hold the current in a solution drops with dilution, whereas molar conductivity increases as the concentration of a solution falls. The increase in total volume containing one mole of the electrolyte causes the rise in molar conductivity.
Q9) State Kohlrausch law.
A9) The equivalent conductivity of an electrolyte at infinite dilution is equal to the sum of the conductance’s of the anions and cations, according to Kohlrausch's law.
The conductance of a volume of solution containing one mole of electrolyte retained between two electrodes with the unit area of cross-section and distance of unit length is the molar conductivity of a solution at a certain concentration. The molar conductivity of a solution increases as the concentration of the solution decreases. The increase in total volume containing one mole of the electrolyte causes the rise in molar conductivity. The molar conductivity is known as limiting molar conductivity, m°, as the electrolyte concentration approaches zero.
While comparing the values of limiting molar conductivities of different strong electrolytes, Kohlrausch noticed some patterns. Kohlrausch proposed that the “limiting molar conductivity of an electrolyte can be expressed as the total of the individual contributions of the electrolyte's anions and cations” based on his observations. This law is known as the Kohlrausch law of independent ion migration. For example, knowing the limiting molar conductivities of sodium ion and chloride ion can help estimate sodium chloride's limiting molar conductivity, m°. The following are some of the most important uses of Kohlrausch's law of independent ion migration: The Kohlrausch law can be used to calculate the limiting molar conductivities of any electrolyte. At increasing concentrations, weak electrolytes have lower molar conductivities and a lower degree of dissociation. For weak electrolytes, the graph between molar conductivity and c1/2 (where c represents the concentration) is not a straight line. At lower concentrations, the molar conductivity of a weak electrolyte increases dramatically. As a result, by extrapolating molar conductivity to zero concentration, m° cannot be achieved as a limiting molar conductivity. As a result, for weak electrolytes, we apply the Kohlrausch law of independent ion migration to determine the limiting molar conductivity, m°. The Kohlrausch law can also be used to calculate the value of the dissociation constant from the value of molar conductivity, as well as to limit molar conductivity for a weak electrolyte at a given concentration.
=/ (E mo)
When dissociation is complete at infinite dilution, each ion contributes a definite amount to the electrolyte's equivalent conductance, regardless of the nature of the ion with which it is associated, and the value of equivalent conductance at infinite dilution for any electrolyte is the sum of contributions of its constituent ions," i.e., anions and cations. As a result
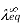 =
=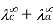
Where,
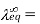 Equivalence Conductivity at Infinite Dilution
Equivalence Conductivity at Infinite Dilution
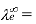 Conductivity of Cation
Conductivity of Cation
 Equivalence Conductivity of Anion
Equivalence Conductivity of Anion
According to Kohlrausch’s law. “Conductivity of ions is constant at infinite dilution and it does not depend on nature of co-ions.”
For AxBy type electrolyte,
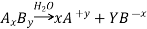
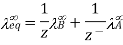
Here Z+ and Z- are the charges present on cation and anion.
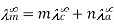
Here m and n are the number of moles of cations and anions.
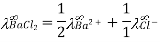
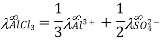
Q10) Give uses of Kohlrausch law.
A10)

Q11) Explain Calculation of Degree of Dissociation.
A11) According to the Arrhenius hypothesis of electrolytic dissociation, the increase in molar conductivity with dilution is entirely due to a rise in electrolyte dissociation, with the molar conductivity at infinite dilution being the highest since dissociation is nearly complete.
As a result, if is the molar conductivity of a solution at any concentration C and is the molar conductivity at infinite dilution (i.e. 0 concentration), we get
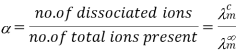
This link, however, is only observed to remain true for weak electrolytes. Kohlrausch's law, as mentioned in the first use, can be used to compute the value of for weak electrolytes.
Q12) Explain Debye-Huckel –Onsager equation.
A12) Peter Debye and Erich Hückel proposed the Debye–Hückel hypothesis as a theoretical explanation for departures from ideality in electrolyte and plasma solutions. It's a linearized Poisson–Boltzmann model that uses a very simple electrolyte solution model but nevertheless gives accurate mean activity coefficient predictions for ions in dilute solution. The Debye–Hückel equation is a good place to start when dealing with non-ideality in electrolyte solutions.
An ideal solution in the chemistry of electrolyte solutions is one whose colligative qualities are proportionate to the solute concentration. Real-world solutions may deviate from this idealised state. The idea of activity was created to accommodate these effects in the thermodynamics of solutions: the properties are thus proportional to the activities of the ions. The activity factor, a, is proportional to the concentration factor, c. The activity coefficient, is the proportionality constant.
All of the ions' activity coefficients are equivalent in a perfect electrolyte solution. Electrolyte solution ideality can only be obtained in very dilute solutions. The non-ideality of more concentrated solutions is caused mostly (but not only) by electrostatic forces that attract ions of opposing charge while repelling ions of the same charge. As a result, unlike in a perfect solution, ions are not distributed evenly throughout the solution
Because an electrolyte solution must contain both positively and negatively charged ions, single ion activity coefficients cannot be studied experimentally. A mean activity coefficient, on the other hand, is defined. For instance, the electrolyte NaCl
In general, a fully dissociated electrolyte with formula AnBm has a mean activity coefficient of
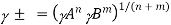
Because the quantity of inter-ionic interaction rises as the electrolyte concentration increases, activity coefficients are themselves functions of concentration. Debye and Hückel established a theory that could be used to compute single ion activity coefficients. The idea might be evaluated against experimental data by computing the mean activity coefficients from them. It was discovered that for "dilute" solutions, it provided great agreement.
A full examination of the assumptions and their limits, as well as the mathematical development and applications, is included in a description of Debye–Hückel theory.
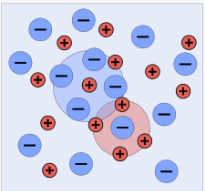
The image is a snapshot of a 2-dimensional segment of an idealised electrolyte solution. Ions are depicted as spheres with a single electrical charge. The solvent (light blue) is depicted as a smooth, unstructured medium. On average, each ion is surrounded by ions with opposite charges rather than ions with similar charges. These ideas were turned into a quantitative theory including ions with charges of z1e+ and z2e, with z being any integer. The main assumption is that deviation from ideality is caused by electrostatic interactions between ions, which are mediated by Coulomb's law: in a medium of relative permittivity r, the force of interaction between two electric charges separated by a distance r is given by

The solute is also considered to be totally dissociated; it is a strong electrolyte, with spherical ions that are not polarised by the electric field. Except insofar as it impacts the ions' effective sizes, ion solvation is ignored.
The solvent's only function is to provide a medium with a constant relative permittivity (dielectric constant).
There isn't any electrostriction here.
Individual ions in the vicinity of a "central" ion can be represented as a statistically averaged cloud of continuous charge density with a minimum closest approach distance.
Each cation is surrounded by a spherically symmetric cloud of other ions, according to the last assumption. There is a net negative charge in the cloud. Each anion is similarly enveloped by a cloud of net positive charge.
Q13) What are the validity of Walden’s rule?
A13) The Stokes-Einstein equation (1) ties the diffusion coefficient to the solution's viscosity, while the Nernst-Einstein equation (2) ties the diffusion coefficient to the equivalent conductivity. 1
D stands for diffusion coefficient, k for Boltzmann’s constant, T for temperature, r for radius, v for viscosity, R for universal gas constant, F for Faraday constant, and z for ion charge. D is removed from the equation to get a relationship between the electrolyte's equivalent conductivity and viscosity. Walden's Rule is the name given to this statement. 1
According to Walden's Rule, the product of a particular electrolyte's limiting equivalent conductivity and viscosity at infinite dilution is a constant at a given temperature. This can be written as an equation, where 0 represents the limiting molar conductivity and 0 or/0 represents the viscosity. 1
To explain how big neutral molecules influence ion limiting mobilities in solution.
Sucrose and other large molecules were used. The sucrose solutions' viscosities were calculated as a percentage. Because viscosities change with temperature, the solutions were held at 20.0°C 0.9.8°F. Various masses of sucrose were dissolved in various quantities of distilled water to produce a spectrum of sucrose solutions with different viscosities: 5%, 10%, 20%, 30%, and 50%. For instance: 10 g sucrose was dissolved in 90 ml distilled water to make a 10% sucrose solution. The solutions were prepared as described before, with the exception that the sucrose and distilled water were used in a weight-to-weight ratio, and the density of water at 20°C is 0.9982g/cm 3. 2
Salts containing various cations and anions of varying concentrations could be added to sucrose solutions of various viscosities. In the initial experiment, tetramethylammonium iodide was employed as the additional salt. Tetramethylammonium iodide concentrations of 0.01, 0.03, 0.05, 0.07, and 0.09 moldm -3 were tested. 3 The salts were added to the sucrose solutions and stirred until they were completely dissolved. A Janeway conductivity metre can be used to determine the conductivity of the solutions (Table 3). This metre can also be used to monitor the temperature of the solutions. Various cations and anions have different trends, which can be seen. Different organizations investigated various salts at varied viscosities.
Q14) What are the evidences found in Favour of Ionic Theory?
A14) A large number of experimental observations are available which support Arrhenius theory. A few of them are given below:
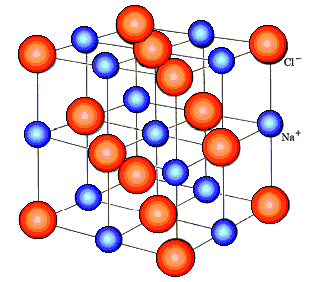
● Ions Present in Solid Electrolytes
Electrolytes are made up of ions, according to X-ray diffraction research. A crystal of NaCl, for example, does not contain NaCl units but rather Na+ and Cl- ions. Each Na+ ion has six Cl- ions surrounding it, and each Cl- ion has six Na+ and Cl- ions around it. In their fused state, ionic compounds act as good conductors. Only if ions are already present in ionic materials is this conceivable.
● Ohm's Law Applicability
Electrolytic solutions, like metallic conductors, follow Ohm's law, which states that the current flowing conductor's strength is proportional to the potential difference (E) applied across the conductor and inversely proportional to the conductor's resistance. I = E/R is a mathematical formula.
Only if ions are already present in the solution and no part of the current has a direct influence on the ions is this possible.
● Ionic Reaction
Well-known inorganic chemistry processes provide evidence for the presence of ions in aqueous electrolyte solutions. When Ag+ ions come into contact with chloride ions, a white precipitate of silver chloride forms.
When AgNO3 solution is introduced to CCl4, CHCl3, or C2H5Cl, however, no precipitation occurs because these compounds are non-electrolytes and do not provide Cl- ions in solution.
Because no ionisation of the acid happens in the common reaction, an acid that gives all tests of H+ ions in aqueous solution does not give the same tests when dissolved in any organic solvent.
● Heat of Neutralization
The heat released when one gramme equivalent of a strong acid is neutralised by one gramme equivalent of a strong base is always the same, i.e. 13.7 kcal. This can be explained using the Arrhenius hypothesis, which states that when an acid is dissolved in water, it produces H+ ions and OH- ions, and the neutralisation process involves the common reaction.
13.7 kcal = H+ + OH- H2O
As a result, the heat of neutralisation is the heat of forming H2O from H+ and OH- ions.
● Abnormal Colligative Properties
The anomalous behaviour of electrolytes toward colligative qualities can be described using ionic theory. The number of molecules actually dissolved when an electrolyte is dissolved in water is related to ionisation. The fact that you can't Hoff,
Is always greater than one, I = 1 + (n-1) where 'n' is the number of ions created by ionisation of one electrolyte molecule and’ is the degree of ionisation.
● Colour of Solution

The electrolytes in solution's colour. CuSO4 is blue in solution due to the presence of Cu2+ ions, if any is owing to their ions. Because of the presence of ions, potassium permanganate (KMnO4) appears purple in solution.
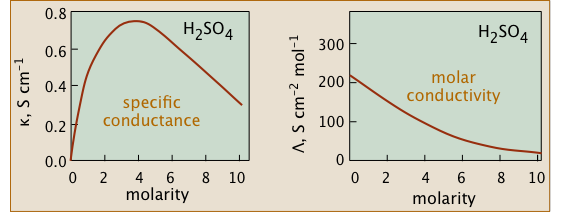
Q15) Verify this statement “Conductivity diminishes as concentrations increase”?
A15) We might expect the conductivity of a solution to be precisely proportional to the concentrations of ions in the solution because ions are charge carriers. If the electrolyte is completely dissociated, the conductivity should be proportional to the concentration of the electrolyte. However, this ideal behaviour is never observed; rather, the conductivity of all electrolytes decreases as concentration rises.
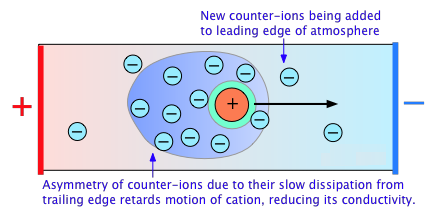
Electrolytic solutions' non-ideality is reflected in their colligative properties, particularly freezing-point depression and osmotic pressure. The presence of the ionic atmosphere, which was mentioned above, is the fundamental cause of this. We would expect their charges to partially cancel, limiting their inclination to migrate in response to an applied potential gradient, to the extent that ions with opposite charge signs are more likely to be closer together.
The fact that an ion's counter-ion cloud cannot keep up with it as it migrates through the solution has a secondary consequence. Instead, on the leading edge of the motion, new counter-ions are constantly obtained, while older ones are left behind on the opposite side. Because the lost counter-ions take some time to disperse, there are always more counter-ions on the trailing edge. The ensuing asymmetry of the counter-ion field retards the central ion, lowering its rate of migration and therefore its contribution to the solution's conductivity.
P. Debye and W. Huckel developed a quantitative treatment of these effects in the early 1920s, which was built upon by Ostwald a few years later. This work was one of the most important advances in physical chemistry in the first half of the twentieth century, and it established a solid theoretical foundation for the behaviour of electrolytic solutions. Even yet, for most ions, the Debye-Huckel theory fails at concentrations greater than 10–3 M L–1.