Unit - 4

Electrochemistry-II

Q1) What is Concentration cell?

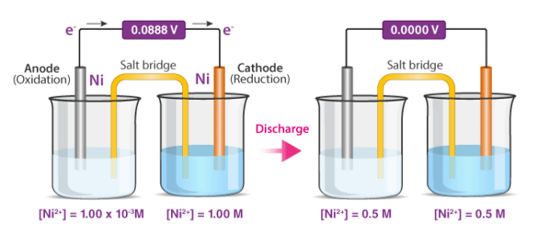
A1) Concentration cells are electrochemical cells that are made up of two half-cells with identical electrodes but different concentrations. The more concentrated half cell is diluted as the cell as a whole seeks to achieve equilibrium, and the lower concentration half cell has its concentration boosted via electron transfer between these two half cells. As a result, a potential difference is formed as the cell approaches chemical equilibrium. Below is a comprehensive diagram of a concentration cell and the discharge process.

Q2) Explain the Types of Concentration Cells.

A2) Concentration cells can be classified into two types, namely:

1. Electrode Concentration Cells
2. Electrolyte Concentration Cells

Electrode Concentration Cells

Each half-cell is made up of identical solutions that serve as electrolytes. The concentration of the electrode in the half-cells, however, differs (the electrodes are made up of the same material).

A cell consisting of two hydrogen electrodes that are subjected to varied pressures but are submerged in the same solutions is an example of this sort of cell (containing hydrogen ions).

Electrolyte Concentration Cells

These cells are made up of identical electrodes immersed in electrolyte solutions of variable concentrations. The electrolyte in these cells tends to diffuse from higher concentration solutions to lower concentration solutions.

A cell with a Zn/Zn2+(0.1M) anode and a Zn2+(0.01M)/Zn cathode is an example of this type of cell. The reduction of Zn2+ ions into metallic zinc at the cathode causes electron transport from the anode to the cathode in this cell.

Q3) What are the Components of the Concentration Cells?

A3) Salt Bridge

The salt bridge is the ideal method for separating the two half-cells while also providing an ion transfer pathway. Ions passing via electric lines would react with them. In the absence of a salt bridge, electrons from the incoming flow of electrons from the other half cell would pile up in one half cell.

A cell's two compartments must be divided so that they do not combine, yet they cannot be entirely separated without allowing ions to pass through. A wire could not be used to connect the two compartments because it would react with the ions flowing from one to the other. As a result, a salt bridge is an essential component of a concentration cell. It solves the major issue of electrons accumulating excessively in the right beaker. Electrons are migrating from the left side, or left beaker, to the right side, or right beaker, causing this accumulation. A salt bridge can take several forms, including a salt solution in a U-tube or a porous barrier (direct contact). By pushing ions to the left side, or left beaker, it balances the charge. The salt bridge is indicated by the double lines in the textual expression that shows what happens in specific reactions. As an example, consider the following:

Cu2+(1 M) |Cu2+(1 M) |Cu2+(1 M) |Cu2+(1 M) |Cu2+(1 M) |Cu2+(1 M) |Cu2+(1 M) |Cu

The salt bridge is represented by the double lines between the Zn2+(1 M) and the Cu2+(1 M). The single lines, on the other hand, do not depict bridges; they depict phase transitions, such as from solid zinc to liquid zinc solution. This is not improper if there is a comma where you would expect to see a single line. It simply means that no phase transitions took place.

Electrode

The cathode (right side) and anode (left side) are the two electrodes (left side). The anode loses electrons and is where oxidation takes place, whereas the cathode is where electrons collect and reduction takes place.

Voltmeter

The voltmeter is used to determine the cell's potential. Electromotive force is another term for cell potential (or EMF). In most cases, the voltmeter is situated halfway between the two half-cells.

To summarise, a concentration cell is a galvanic cell in which the half-cells contain the same chemical but at varying concentrations. While advancing towards chemical equilibrium, these cells produce a minor potential difference that can be monitored with a voltmeter.

Q4) Explain the Uses of Concentration Cells.

A4) A pH metre is a sort of concentration cell that employs a concentration cell's basic setup to determine the pH, or acidity/basicity, of a specific solution. It consists of two electrodes as well as a voltmeter. One of the electrodes, the glass electrode, is made up of two parts: a metal wire (usually silver chloride) and a semi-porous glass section filled with a potassium chloride solution with a pH of 7 that surrounds the AgCl. The reference electrode, which has a potassium chloride solution encircling a potassium chloride wire, is the other electrode. The second electrode's aim is to provide as a comparator for the solution being evaluated. When the glass electrode comes into touch with a solution with a variable pH, the hydrogen ions react with the metal ions, creating an electric potential. The voltmeter, which is attached to the electrode, then measures this potential. The higher the voltage, the more hydrogen ions are present in the solution, indicating that it is more acidic.

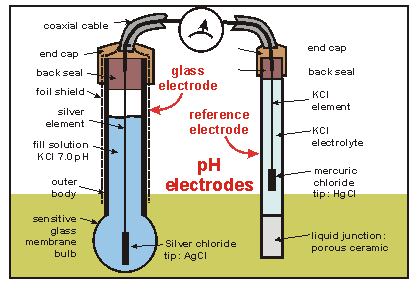
An example of a pH meter

Junction potential:

Any interface, or junction, where there is a charge separation creates a potential. When a metal electrode comes into touch with a solution containing its cation, for example, a potential can arise. The Nernst Equation can be used to describe this type of potential.

When electrolyte solutions of different composition are separated by a boundary, such as a membrane or a salt bridge, a potential can form (a gel-filled tube containing an inert electrolyte that connects half-cells to allow charge neutrality to be maintained).

The two solutions could have the same ions but at different concentrations, or they could have completely different ions. The mobilities of these ions vary, which implies they travel at various speeds.

A porous glass frit, for example, could divide two NaOH solutions:

0.01 M NaOH / NaOH (0.001 M)

OH- travels at a rate of about 5 times that of Na+...

. . . Developing of a potential at the interface, or boundary, between the two solutions.

So now for an electrochemical cell containing a salt bridge, the cell potential is actually:

Ecell=Ecathode−Eanode+Ejunction

Typical liquid junction potentials range from a few mV to 40 mV, depending on the electrolyte solutions' identities and concentrations.

The junction potential of a simple cell, such as the one described on the preceding page, may be determined using the ion mobilities. Most practical electrochemical cells, on the other hand, are more sophisticated. The standard addition quantitation method can be used to adjust for or eliminate mistakes caused by a junction potential. A potential measurement is performed on a solution containing only the analyte ion in this case. After that, a known volume of standard ion solution is “spiked” into the solution, and a second potential measurement is taken. This approach can be repeated for a number of spikes (multiple standard addition method). It's safe to presume that adding the standard has no effect on the junction potential. In the Experimental section of this topic, you can read more about this quantification method in the Chloride Experiment.

Q5) What is Potentiometric Titration? Explain its Principle and Titration Method.

A5) It is the technique for determining the quantity of a specific test substance by adding titrant in small increments until the entire test substance reacts. The potential difference between the two electrodes (the reference and indicator electrodes) is measured after the titration process in conditions when the thermodynamic equilibrium is maintained and the current running through the electrodes does not affect it.

Potentiometric Titration Principle

A laboratory method for determining the concentration of a particular analyte is potentiometric titration. It's utilized to figure out what acids are. A chemical indicator is not used in this procedure. Instead, the electric potential is measured across the substance.

Potentiometric Titration Method

Two electrodes are used in potentiometric titration: an indication electrode and a reference electrode (generally a hydrogen electrode or a silver chloride electrode). The indicator electrode and the ions of the analyte, which is usually an electrolyte solution, form a half-cell. The reference electrode forms the other half-cell.

The formula below can be used to compute the overall cell potential.

Ecell = Eind – Eref + Esol 

Esol is the potential difference between the indication and reference electrodes in the electrolyte solution.

Every interval where the titrant is measured and applied, the entire cell potential, Ecell, is determined. Now, as shown below, a graph is drawn with the Potential difference on the Y-axis and the volume on the X-axis.

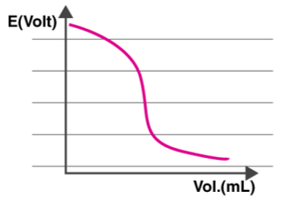
The electric potential of the cell is proportional to the concentration of ions in contact with the indicator electrode, as shown in the graph. As a result, the Ecell is measured after each titrant addition.

Q6) Explain the Types of Potentiometric Titration.

A6) Acid-base titration, redox titration, complexometric titration, and precipitation titration are the four types of titrations that fall under the category of potentiometric titration. Below is a quick summary of each of these forms of titration.

Acid-Base Titration: This sort of potentiometric titration is used to estimate the concentration of a given acid/base by neutralising it precisely with a known-concentration standard solution of base/acid.

Redox Titration: A redox reaction occurs between the analyte and the titrant in this sort of potentiometric titration. The treatment of an iodine solution with a reducing agent to form the iodide ion is an example of this type of titration (a starch indicator is used to get the endpoint).

Complexometric Titration: Chelatometry is another name for this sort of titration. A coloured complex is created in this procedure, signifying the titration's end point. This approach is used to identify a metal ion combination in a solution.

Precipitation Titration: An insoluble precipitate is created as a result of an interaction between the analyte and the titrant in this type of titration. When the addition of the titrant no longer generates a precipitate, the titration is complete.

Q7) Explain the Electrical properties of atoms and molecules.

A7) Atoms 

The majority of the Universe is made up of matter and energy. The capacity to work is defined as energy. Matter has mass and takes up room. Basic elements make up all matter, and they can't be split down into compounds with distinct chemical or physical properties. Elements, for example, are compounds made up of only one type of atom. Diamond and graphite are both made up of carbon atoms. Gold atoms are the only type of atom in pure (24K) gold. Atoms are the smallest particles that can be separated into an element. The notion of the atom was conceived by ancient Greek philosophers, who saw it as the primordial particle that could not be broken down. We now know that the atom is divisible, often releasing enormous energies as in nuclear explosions or (in a controlled manner in) thermonuclear power plants, thanks to the work of Enrico Fermi and his colleagues.

During the 1800s, subatomic particles were discovered. For our purposes, we'll focus on only three of them, which are included in Table 1. Each atom has at least one proton, which is located in the centre (or nucleus) of the atom. Protons have a positive charge and a mass of about 1 atomic mass unit (amu). The amount of protons in each element varies, for example, Hydrogen has one proton whereas Helium has two.

The neutron is found in the atomic nucleus as well (except in Hydrogen). The neutron is a neutral particle with a mass of little more than 1 amu and no charge. According to some scientists, the neutron is composed of a proton and an electron-like particle.

The electron is a tiny particle that exists outside of the nucleus. The specific position of electrons is difficult to nail down since they move at speeds close to the speed of light. Orbitals, or places where electrons have a high statistical likelihood of appearing, are occupied by electrons. An electron has a charge of -1. It has a very small mass (approximately 1800 electrons are needed to equal the mass of one proton).

Table 1 shows the subatomic particles that are used in biology.

The number of protons in an atom is known as its atomic number. Each element has its own distinct personality. The number of protons and neutrons in an atom is measured by its atomic mass (also known as its atomic weight). Isotopes are atoms of the same element with different quantities of neutrons (but the same atomic number). Figures 1 and 2 show how isotopes can be used to establish ancient peoples' diets by calculating the amounts of isotopes in mummified or fossilised human tissues. Isotopic tracers can be used to interpret biochemical processes. Radioactive isotopes can be used to determine the age of fossils and artefacts, either directly on the fossil (if it is young enough) or on the rocks that surround the fossil (for older fossils like dinosaurs). Isotopes are also employed in medical diagnostic and therapeutic processes as a source of radiation.

1st Figure It's worth noting that each of these hydrogen isotopes only has one proton. Isotopes differ in the number of neutrons they have rather than the number of protons they have.

Some isotopes are radioisotopes, meaning they decay spontaneously and emit radiation. Other isotopes have a long half-life. Carbon-14 (symbol 14C) and deuterium are two radioisotopes (also known as Hydrogen-2; 2H). 12C and 1H are stable isotopes.

Q8) Write Short note on Chemical Bonding.

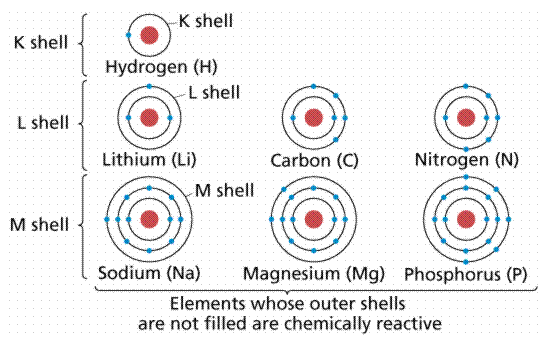
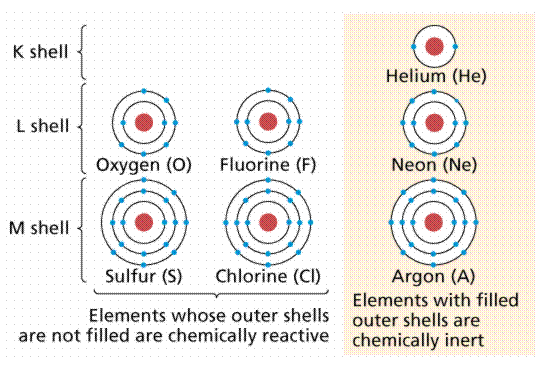
A8) Chemists grouped the then-known elements according to chemical bonding during the nineteenth century, observing that one group (the far-right column on the Periodic Table, known as the Inert Gases or Noble Gases) tended to occur in elemental form (in other words, not in a molecule with other elements). It was eventually discovered that this group of elements has outer electron shells with two (as in Helium) or eight (Neon, Xenon, Radon, Krypton, and so on) electrons.

In general, atoms gain or lose outer electrons to reach a Noble Gas outer electron shell configuration of two or eight electrons for the atoms we are likely to encounter in biological systems. The amount of electrons acquired or lost is unique to each element, and it ultimately affects the number and types of chemical bonds that can be formed by its atoms. Figure 6 depicts atomic diagrams for numerous atoms.

Figure: Atomic diagrams showing how the outer electron shells are filled.

Q9) Explain the Basic ideas of electrostatics.

A9) Electrostatics in chemistry:

In weak intermolecular interactions, electrostatics plays a crucial role. The goal of this series is to comprehend these electrostatic properties. The fundamental concepts of electrostatics as applied to atoms and molecules are presented in this article. The electric field and potential generated by a set of discrete and continuous charge distributions, as well as their graphic depiction, are explored. Electrostatic fundamental theorems are also summarised.

Introduction

Atoms and molecules are the operational building units of matter, according to chemists. The total energy of an atom is dominated by the electrostatic interaction energy between the positively charged nucleus and negatively charged electrons. Molecules are formed when atoms come together. The chemistry of the covalent bond, or molecular chemistry, is concerned with the structures, characteristics, and reactions of these molecules. Supra11UJlecular chemistry, which is defined as chemistry beyond the molecule, is a novel discipline of chemistry that deals with complexes of two or more molecular subunits that has emerged in recent years. The fundamental issue of molecular recognition has various applications in the chemical sciences, including analytical chemistry, bioinorganic and bioorganic chemistry, catalysis, and enzyme chemistry, among others. Electrostatics is well acknowledged to play a key role in these recognition processes. As a result, an understanding of electrostatics is required for a proper background in supramolecular science. Basic molecular electrostatics and its applications to weak intermolecular interactions will be explored in this series of papers.

Electrical Charges and Coulomb's law

The concept of an electric charge underpins the development of electrostatics. The following are some experimental facts about electric charges: I There are two types of electric charges in nature. Positive and negative charges are the terms for these two types of charges (the present labels of positive and negative to charges of proton and electron, respectively, are indeed a historical accident).

Ii) The force between two-point charges is proportional to their product and inversely proportional to the square of their distance, and it acts along the line that connects them.

The above experimental results are combined together in Coulomb's law

Here F2, l is the force acting upon q1, r1 and r2 are the position vectors of ql and q2 respectively, with respect to an arbitrary origin 0 as shown in Figure 1.

The presence of other point charges has no effect on the electrostatic forces between two-point charges. When extra point charges are introduced, the force F2, l (Equation 1) remains unchanged. These forces are pair-wise additive, and the total force Fl owing to point charges q' q3.... Qn on the point charge q1 is given by

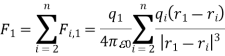
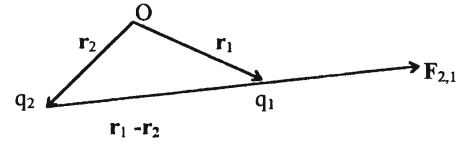
Figure shows the force F2, 1 exerted by q2 on q1' in a schematic diagram. The charges q1 and q2 are respectively situated at r 1 and r 2.

The superposition principle refers to the additive behaviour of electrostatic forces.

Q10) What is Gauss’s Law?

A10) Gauss's law gives a mechanism for calculating any electric field; however, it is only useful for fields with highly symmetric constant charge distributions. The net electric flux through any closed surface, real or imaginary, is equal to the net electric charge enclosed within that surface divided by. As a result, if a closed surface has no charge, there are as many flux lines entering the surface as there are exiting it. The gaussian surface is the imaginary surface required to implement Gauss's law. In terms of algebra,

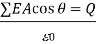
Or in integral form, 

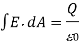
Where is the permittivity constant and is the angle between the direction of E and the outward direction of normal to the surface.

Consider the computation of a point charge's electric field. Figure depicts a point charge, its field direction, and a gaussian surface. Because the electric field is directed outward and perpendicular to the gaussian surface, is 90 degrees, and cos = 1. The law of Gauss is

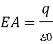
Substitute in the area of a sphere, and the left side reduces to

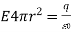
Or

It is the same formulation as Coulomb's law and the force-based description of an electric field.

The expression for the field due to a thin conducting shell of charge is deduced as follows. The electric fields for (a) a radius (R) shell, (b) the gaussian surface for outside the shell, and (c) the gaussian surface for within the shell (c) of radius are shown in Figure. (r).

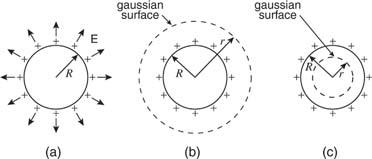
A charged R-radius spherical shell. (b) A gaussian sphere having a radius greater than R. (c) A sphere with radius r R with a gaussian surface.

When outside the shell of charge, as in Figure (a), the left side of Gauss's equation reduces to the following expression for the same reasons given for a point charge:

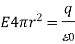
Therefore, 

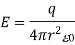
As a result, the electric field outside a sphere of charge is the same as if the same amount of charge were concentrated in the sphere's centre.

There is no electric field inside the uniformly charged spherical shell because the gaussian surface inside the sphere encloses no charge. Because all of the charge in a solid conductor is concentrated on the surface, the same proof applies. The charge will not be evenly spread over an uneven form since the electric field within even an irregularly shaped conductor is zero. The charge will tend to collect on projecting areas on the conductor's exterior.

Q11) What is Electrostatics of dielectric media?

A11) Polarization:

Because it is made up of neutral atoms and molecules, the terrestrial environment is characterised by dielectric media (e.g., air and water) that are electrically neutral for the most part. When the atoms and molecules that make up such medium are exposed to an electric field, they tend to polarise, or produce electric dipole moments. Because it is made up of neutral atoms and molecules, the terrestrial environment is characterised by dielectric media (e.g., air and water) that are electrically neutral for the most part. When the atoms and molecules that make up such medium are exposed to an electric field, they tend to polarise, or produce electric dipole moments. Suppose that when a given neutral molecule is placed in an electric field, E, the centre of charge of its constituent electrons (whose total charge is  ) is displaced by a distance 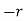 with respect to the centre of charge of its nucleus (whose charge is  ). The dipole moment of the molecule is then 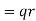 . (See Section 2.7.) If there are  such molecules per unit volume then the electric polarization 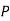 (i.e., the dipole moment per unit volume) is given by  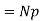. More generally,

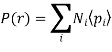
Where  is the average dipole moment of the  th type of molecule in the vicinity of point, and 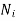 is the average number of such molecules per unit volume at  .

It is easily demonstrated [e.g., by integrating Equation (201) by parts, and then comparing the result with Equation (162)] that any divergence of the polarization field,  , gives rise to a charge density, 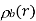 , in the medium. In fact,

This density is distinguished from the charge density owing to free charges, which reflects a net excess or deficit of electrons in the medium, by bound charges (i.e., charges that emerge from the polarisation of neutral atoms). As a result, the medium's overall charge density, is

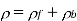
Both terms on the right-hand side of this equation represent genuine physical charge, it should be noted. Nonetheless, distinguishing between bound and free charges is useful, especially when calculating the energy associated with electric fields in dielectric media.

Gauss' law takes the differential form

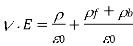
This expression can be rearranged to give

where

Is termed the electric displacement (which should not be confused with dipole moment per unit area--see Section 2.8), and has the same dimensions as P (i.e., dipole moment per unit volume). The divergence theorem tells us that

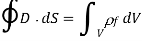
In other words, the total free charge enclosed within a closed surface equals the flux out of that surface. The electric displacement, unlike the electric field (which is the force acting on a unit charge) or the polarisation (which is the dipole moment per unit volume), has no apparent physical meaning. This variable is only included because it allows us to calculate electric fields in the presence of dielectric materials without previously knowing the distribution of bound charges. However, this is only possible if and are connected by a constitutive relation. It is common practise to assume that the induced polarisation, is proportional to the electric field, and that

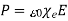
Where 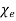 is termed the medium's electric susceptibility. It follows that

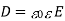
Where the dimensionless quantity

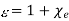
Is known as the relative dielectric constant or relative permittivity of the medium. It follows from Equations (501) and (505) that

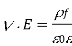
Q12) Explain Energy Density Within Dielectric Medium.

A12) Consider a system of free charges embedded in a dielectric medium. The increase in the total energy when a small amount of free charge 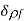 is added to the system is given by

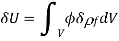
Where the integral is taken over all space, and 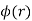 is the electrostatic potential. Here, it is assumed that the original charges and the dielectric are held fixed, so that no mechanical work is performed. It follows from Equation (501) that

where δD is the change in the electric displacement associated with the charge increment. Now, the above equation can also be written

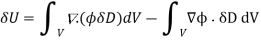
Giving

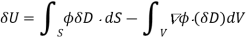
Where use has been made of the divergence theorem. If the dielectric medium is of finite spatial extent, then we can neglect the surface term to give

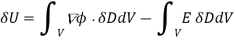
This energy increment cannot be integrated unless 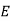 is a known function of. Let us adopt the conventional approach, and assume that , where the dielectric constant  is independent of the electric field. The change in energy associated with taking the displacement field from zero to 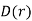 at all points in space is given by

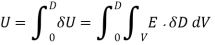
Or

Which reduces to

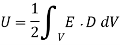
Thus, the electrostatic energy density inside a dielectric is given by

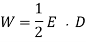
This is a well-known result that is frequently cited in textbooks. It's vital to remember, however, that the preceding formula only applies to dielectric medium where the electric displacement, varies linearly with the electric field.

Q13) What is Clausius-Mossotti relation.

A13) The Clausius-Mossotti connection [1] [2] in physics links a dielectric's relative permittivity r to the polarizability of the atoms or molecules that make up the dielectric. Relative permittivity is a bulk (macroscopic) property of matter, while polarizability is a microscopic characteristic; thus, the relationship connects a directly observable macroscopic feature with a tiny molecular property.

For dielectric matter made up of atoms or (non-polar) molecules, the Clausius-Mossotti equation is used.

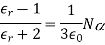
Where 0 denotes the electric constant (vacuum permittivity) and N denotes the number density (number of atoms or molecules per volume).

A dielectric's index of refraction, n, is given by

Where we used that the relative magnetic permeability r is fairly close to unity for most dielectric materials. The Lorentz-Lorenz relation is obtained by substituting this value of n.

Q14) Explain Lorentz-Lorenz relation.

A14) The Lorentz-Lorenz relation is a physics equation that describes the relationship between the index of refraction n and the density of a dielectric (non-conducting matter),

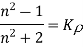
The polarizability of the molecules that make up the dielectric determines the proportionality constant K.

The relationship is named after Hendrik Antoon Lorentz, a Dutch physicist, and Ludvig Valentin Lorenz, a Danish physicist.

The proportionality factor K (m3/kg) for a molecular dielectric made up of a single type of non-polar molecules is,

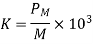
Where M (g/mol) is the molar mass (previously known as molecular weight) and PM (m3/mol) is the molar mass (previously known as molecular weight) in SI units:

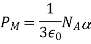
NA is Avogadro's constant, is one molecule's molecular polarizability, and 0 is the electric constant (permittivity of the vacuum). The molecular polarizabilities are assumed to be additive in this expression for PM; if this is not the case, the expression can still be employed if is replaced by an effective polarizability. The factor 1/3 is based on the idea that a single molecule inside the dielectric experiences a spherical field from the surrounding media. Because / 0 has the dimension volume, K has the dimension volume per mass.

In non-rationalized centimeter-gram-second units (Gaussian units):

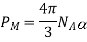
K (as well as 0, which is not defined in Gaussian units) lacks the component 103.

A temperature-dependent contribution owing to dipole alignment must be added to K for polar molecules.

Q15) How are polarizabilities measured experimentally?

A15) Most typical spectroscopies that yield a whole spectrum, a tensor, or a scalar value have a dedicated apparatus that is reasonably self-contained and non-standard. Benchtop FT-IR spectrometers, for example, provide (linear) IR spectra, while FT-NMR spectrometers (capable of multiple experiments) provide NMR chemical shifts, and so on. The (electric dipole) polarizability, which "is defined as the ratio of the induced dipole moment pp of (a molecule) to the electric field EE that produces this dipole moment" and is important for designing optical materials, is one spectroscopic property that serves as a benchmark for electronic structure theory and is important for designing optical materials:

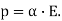
This refers to how easy it is to move a system's charge density or electron cloud around physically. It's a symmetric rank-2 tensor, to put it another way:

Because the supplied electric field may have three distinct Cartesian coordinates and the system being measured may have an anisotropic response to it Calculating the tensor can take a long time in some circumstances, although the process is well-understood and there are standardised ways for doing it. However, I'm not sure how it's measured in a lab setting. The Lorentz-Lorenz equation exists (rearranged),

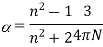
It connects a system's or medium's polarizability to its refractive index nn. There is also the Clausius-Mossoti relation, which relates the dielectric constant ϵϵ to the polarizability, as the refractive index and (complex) dielectric constant are related:

n∝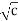

This leads me to believe that using a refractometer to determine the refractive index is the preferred method of determining polarizability.

Is the refractive index the most prevalent way of determining polarizability experimentally? Is it possible to test it directly, or does it have to be through a relationship like the ones listed above?

• Is this relationship valid for both directed (anisotropic) and averaged (isotropic) polarizabilities?
• The refractive index and polarizability are qualities that are frequency dependent. What is the method for determining static (frequency-independent) polarizability? Is it even possible to do so without using extrapolation from a large number of frequency-dependent data points?

Q16) Define Polarizability.

A16) Polarizability helps us better understand how nonpolar atoms and molecules interact with other electrically charged species like ions and polar molecules with dipole moments.

Introduction

In their electron clouds, neutral nonpolar substances exhibit spherically symmetric groupings of electrons. Their electron clouds can be altered in the presence of an electric field (Figure). The polarizability of an atom or molecule determines how easily it can be distorted. The nonpolar molecule or atom gains a dipole moment as a result of the generated distortion of the electron cloud. The following equation relates the induced dipole moment to the polarizability of the molecule or atom and the strength of the electric field:

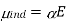
Where E signifies the electric field strength and is the polarizability of the atom or molecule in C m2V-1 units.

Figure: A neutral nonpolar species’ electron cloud is distorted by A.) an Ion and B.) a polar molecule to induce a dipole moment.

Polarizability is related to the interaction of electrons with the nucleus in general. The number of electrons in a molecule influences how tightly the nuclear charge can govern the charge distribution overall. Because there is a significant interaction between the few electrons in the atoms' orbitals and the positively charged nucleus, atoms with fewer electrons will have smaller, denser electron clouds. Atoms with fewer electrons have less shielding, resulting in a stronger interaction between the outside electrons and the nucleus. Because the electrons in these tiny atoms are closely bound, they are not easily polarised by external electric fields. Large atoms with numerous electrons, such as negative ions with extra electrons, on the other hand, are easily polarised. These atoms have huge atomic radii and dispersed electron clouds, which limit the interaction of their exterior electrons with the nucleus.

Q17) Explain Factors that Influence Polarizability.

A17) The following is the link between polarizability and electron density, atomic radii, and molecule orientation:

1. The nuclear charge has less control over charge distribution as the number of electrons increases, resulting in increasing polarizability of the atom.

2. The larger the distance between electrons and nuclear charge, the less control the nuclear charge has on the charge distribution, and hence the larger the atom's polarizability.

3. Except for molecules that are tetrahedral, octahedral, or icosahedral, polarizability can be affected by molecular orientation in relation to an electric field (labelled Orientation-dependent) (labelled Orientation-independent). This is especially true for unsaturated compounds like 2,4-hexadiene, which have areas of electron-dense regions. When the electric field is applied parallel to the molecule rather than perpendicular to the molecule, the greatest polarizability is achieved.

Q18) Explain Polarizability Influences Dispersion Forces.

A18) The weakest intermolecular force is the dispersion force. It's an attracting force that emerges from nonpolar molecules or species' transient dipole moments. When there are instantaneous variations in the electron clouds of nonpolar species, these temporary dipole moments occur. Surrounding molecules are affected by these brief dipole moments, resulting in a chain reaction that produces weak, dipole-induced dipole interactions. The attractive dispersion forces are created by the accumulated dipole-induced dipole interactions. When the temperature is low enough, dispersion forces cause nonpolar substances to condense into liquids and freeze into solids.

Polarizability has the following effects on dispersion forces:

1. The dispersion forces become stronger as polarizability increases. As a result, molecules attract one other more strongly, and the melting and boiling temperatures of covalent substances rise as molecular mass increases.

2. Polarizability has an impact on dispersion forces due to the molecular shape of the molecules involved. Elongated molecules have more easily transported electrons, which increases their polarizability and strengthens the dispersion forces (Figure 22). Small, compact, symmetrical molecules, on the other hand, are less polarizable and have less dispersion forces.

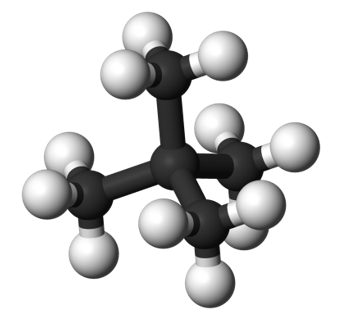
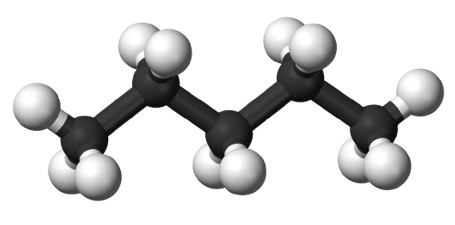
Graph: (top) A more compact and less polarizable molecule is neopentane, which is an isomer of n-pentane. (At the bottom) An example of an elongated molecule that is more easily polarised is n-Pentane.

The following equation, which may be used to measure the interaction between two like nonpolar atoms or molecules, shows the link between polarizability and dispersion forces:

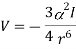
Where

1. r is the distance between the atoms or molecules,
2. I is the first ionization energy of the atom or molecule, and
3. α is the polarizability constant expressed in units of m3.

This expression of αα is related to α′α′ by the following equation:

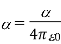
To quantify the interaction between unlike atoms or molecules (A and B) the Equation becomes:

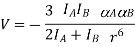
Q19) Write short note on Molecular Dipole Moments.

A19) The three-dimensional geometry and symmetry of increasingly complex molecules with polar covalent connections dictate whether there is a net dipole moment. Dipole moments are vectors in mathematics; they have both a magnitude and a direction. The vector sum of the dipole moments of the individual bonds in a molecule is thus the dipole moment of the molecule. There is no net dipole moment if the individual bond dipole moments cancel out. CO2, a linear molecule (part (a) in Figure 2.2.8), is an example of this. Despite the fact that each C–O bond in CO2 is polar, tests reveal that the CO2 molecule does not have a dipole moment. The two C–O bond dipoles in CO2 cancel because their magnitudes are equivalent and they are orientated at 180 degrees to each other. As a result, despite having a significant charge separation, the CO2 molecule has no net dipole moment. The dipole moments do not cancel each other because the H2O molecule is not linear (part (b) in Figure 2.2.8); it is bent in three-dimensional space. As a result, a molecule like H2O has a net dipole moment. The oxygen, the more electronegative atom, should have the highest concentration of negative charge, whereas the two hydrogens should have the highest concentration of positive charge. H2O can hydrogen-bond to other polarised or charged species, including other water molecules, because of its charge polarisation.

Molecules with Polar Bonds: The bond dipole moments of individual bonds are shown in red. Some molecules with polar bonds have a net dipole moment (HCl, CH2O, NH3, and CHCl3) due to their various three-dimensional structures, but others do not (HCl, CH2O, NH3, and CHCl3) because the bond dipole moments cancel (BCl3, CCl4, PF5, and SF6).