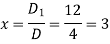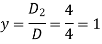Unit 1

Matrices and Determinants

Q1)

A1)

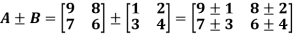
Q2) Add .

A2)

A + B =

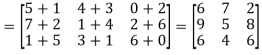
Q3) Multiply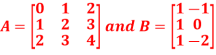

A3)

Then

Q4) Find the inverse of matrix ‘A’ if-

A4)

Here we have-

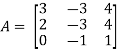
Then

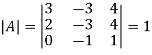
And the matrix formed by its co-factors of |A| is-

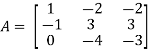
Then

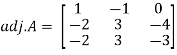
Therefore-

We know that-

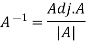
Q5) Find the inverse of matrix ‘A’ by using elementary transformation-

A =

A5)  Write the matrix ‘A’ as-  

A = IA

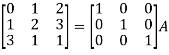
Apply , we get

Apply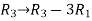

Apply

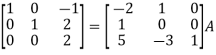
Apply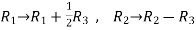

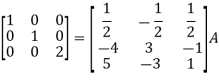
Apply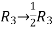

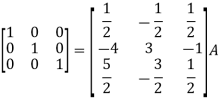
So that,

  =

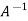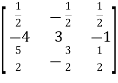
Q6) Find the inverse of matrix ‘A’ by using elementary transformation-

A =

A6)  Write the matrix ‘A’ as-  

A = IA

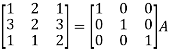
Apply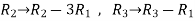

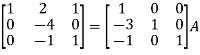
Apply

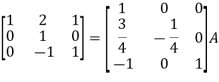
Apply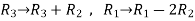

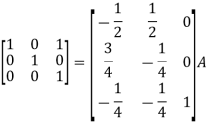
Apply

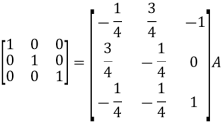
So that

  = 

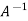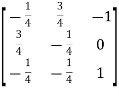
Q7) Find the solution of the following homogeneous system of linear equations,

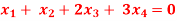
A7) The given system of linear equations can be written in the form of matrix as follows,

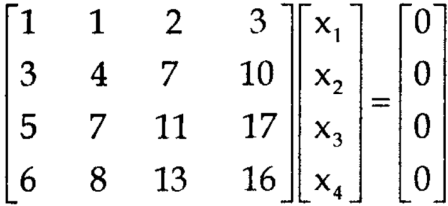
Apply the elementary row transformation,

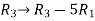
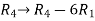  , we get,

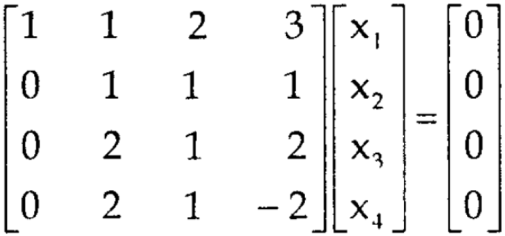
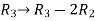
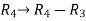    , we get

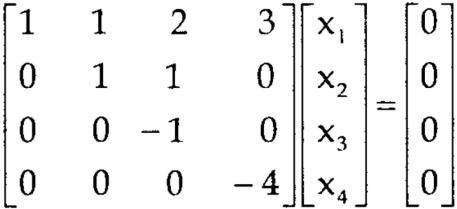
  Here r(A) = 4, so that it has trivial solution,

Q8) Find out the value of ‘b’ in the system of homogenenous equations-

2x + y + 2z = 0

x + y + 3z = 0

4x + 3y +  bz = 0

Which has

(1) trivial solution

(2) non-trivial solution

A8) (1)

For trivial solution, we already know that the values of x , y and z will be zerp, so that ‘b’ can have any value.

Now for non-trivial solution-

(2)

Convert the system of equations into matrix form-

AX = O

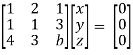
Apply respectively , we get the following resultant matrices

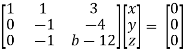
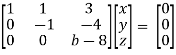
For non-trivial solutions , r(A) = 2 < n

b – 8 = 0

b = 8

Q9) Check the consistency and find the values of x , y and z of the following system of linear equations.

2x + 3y + 4z = 11

X + 5y + 7z = 15

3x + 11y + 13z = 25

A9) Re-write the system of equations in augmented matrix form.

C = [A,B]

That will be,

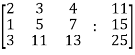
Apply 

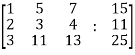
Now apply ,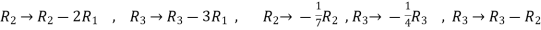

We get,

~~

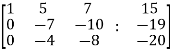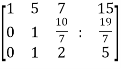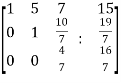
Here rank of A = 3

And rank of C = 3, so that the system of equations is consistent,

So that we can can solve the equations as below,

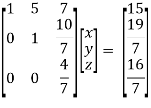
That gives,

x + 5y + 7z = 15  ……………..(1)

y + 10z/7 = 19/7 ………………(2)

4z/7 = 16/7 ………………….(3)

From eq. (3)

z = 4,

from 2,

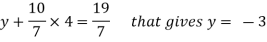
From eq.(1), we get

x + 5(-3) + 7(4) = 15

That gives,

x = 2

Therefore the values of x , y , z are    2 , -3 , 4  respectively.

Q10) Solve the following equations by using Cramer’s rule-

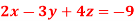
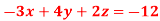
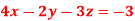
A10)

Here we have-

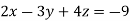
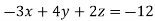
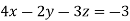
And here-

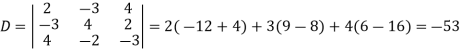
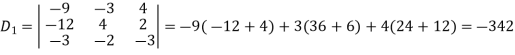
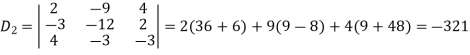
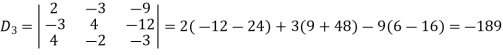
Now by using cramer’s rule-

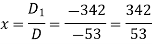
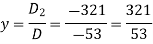
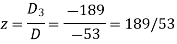
Q11) Solve the following system of linear equations-

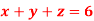
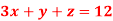
A11)

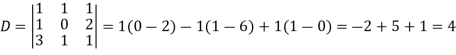
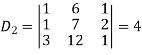
By using cramer’s rule-