Unit 2
Calculus -I
Q1) Explain polynominal function.
A1)
A polynomial in the variable x is a function that can be written in the form-
Here 
are constant.
The term containing the highest power of x are called the leading term
The degree of the polynomial is the power of x in the leading term. degree 0, 1, and 2 are polynomials which are constant, linear and quadratic functions while degree 3, 4, and 5 are polynomials with special names: cubic, quartic, and quintic functions. Polynomials with degree n > 5 are just called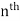 
degree polynomials.
Q2) Find the domain and range of the function f(x) = 
A2)
f(0) = 3/-3 = -1
f(1) = -1
f(2) = -1
f(3) = -1
So that the domain is = {-1, 0, 1, 2, 4,….} and range = {-1, -1, -1, -1,…..}
Q3) find the value of f(2), f(0) and f(3) of the given function-
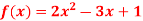
A3)
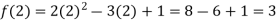
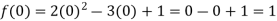
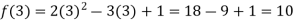
Q4) if f(x) =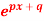 
then prove that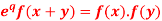 
A4)
By taking LHS-
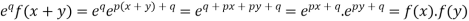
Hence proved
Q5) Differentiate the function f(x) =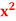 
by using the first principal method.
A5)
We know that-
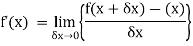
Here
Substituting (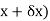
for x gives-
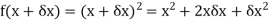
Hence-
Q6) evaluate the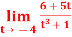 
A6) We can simply find the Solutionution as follows,
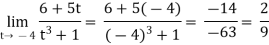
Q7) evaluate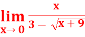 
A7)
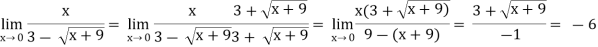
Q8) evaluate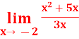 
A8)
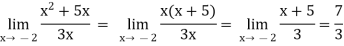
Q9) Find dy/dx of the following functions-
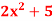
A9)
Let y =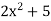 
Then-
And
Let y =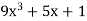 
Then-
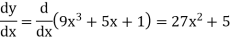
Q10) Differentiate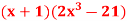 
with respect to x.
A10)
Let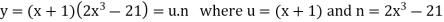 
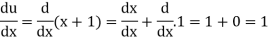
Now
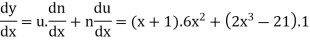
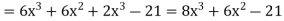
Q11) if 
then find dy/dx.
A11)
Suppose y = u/v where u = x - 1 and v = x + 1
Then
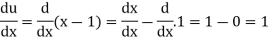
And
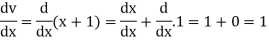
So that-
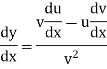
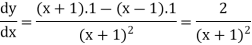
Q12) if y =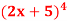 
then find dy/dx.
A12)
Suppose z =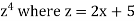 
Now-
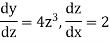
So that-
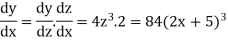
Q13) if y = 
A13)
Suppose y =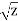 
where z =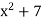 
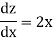
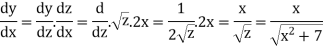
Q14) If y = log loglog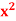
then find dy/dx.
A14)
Suppose y = log u where u = log v and v = log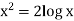 
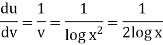
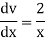
So that-
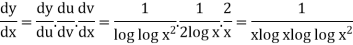
Q15) if y = 
A15)
Let y = log u where u =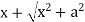 
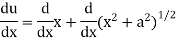
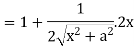
Now
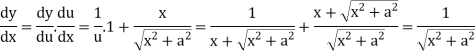
Q16) find the derivative of the function f(x) = 
.
A16)
Let y = f(x) then
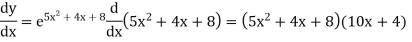
Q17) Find the derivative of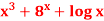 
A17)
Let y =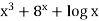 
then-
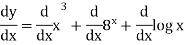
Q18) if y =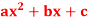 
then find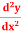 
A18)
Here
Difference with respect to x, we get-
Now
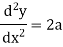
Q19) if y =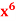 
then find 
.
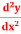A19)
Here
y =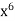 
Then
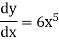
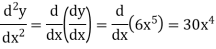
Q20) Examine for maximum and minimum for the function f(x) = 
A20)
Here the first derivative is-
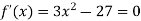
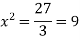
So that, we get-
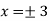
Now we will get to know that the function is maximum or minimum at these values of x.
For x = 3
Let us assign to x, the values of 3 – h and 3 + h (here h is very small) and put these values at f(x).
Then-
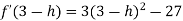Which is negative for h is very small
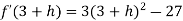Which is positive
Thus f’(x) changes sign from negative to positive as it passes through x = 3.
So that f(x) is minimum at x = 3 and the minimum value is-
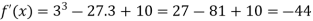
And f(x) is maximum at x = -3.
