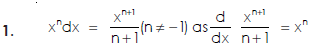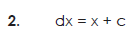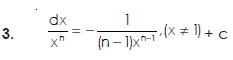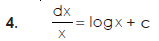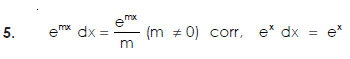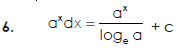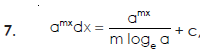Unit 3

Calculus II

Q1) Explain integration.

A1)

Integration is the reverse process of differentiation. It is also called annti-differentiation.

Integration calculus has its own application in economics, Engineering, Physics, Chemistry, business, commerce, etc.

 The integral of a function is denoted by the sign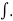

Let the function is y = f(x),

Its derivative is-

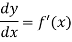
Then

Where c is the arbitrary constant.

For example,

A function,

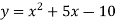
Then, its derivative-

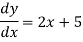
Or

Then-

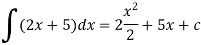
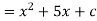
Here c is an arbitrary constant.

Some fundamental integrals-

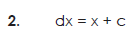
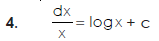
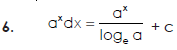
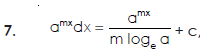
Q2) Find the integral of-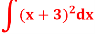
 

A2) We know that-

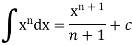
Then

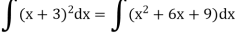
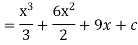
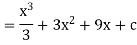
Q3) Find the integral.

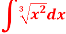
A3)

We know that-

Then

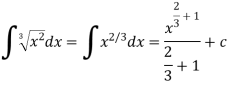
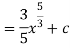
Q4) Evaluate-

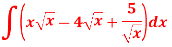
A4)

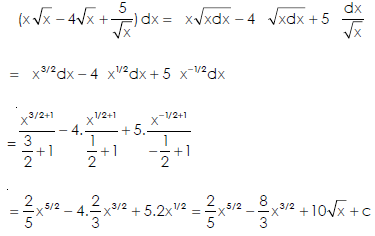
Q5) Evaluate the following integral-

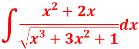
A5)

Let us suppose,

Then-

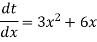
Or

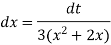
Substituting –

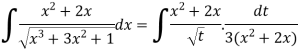
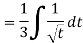
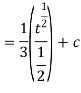
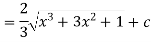
Q6) Evaluate the following integral-

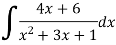
Sol.

Let us suppose-

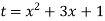
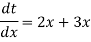
Now

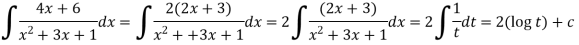
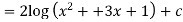
Q7) Evaluate-

A7)

Let,

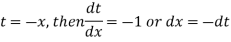
Now substituting-

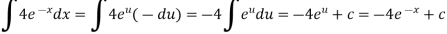
Q8) Evaluate-

A8)

Here according to ILATE,

First function = log x

Second function =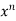

We know that-

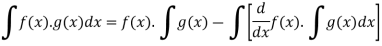
Then-

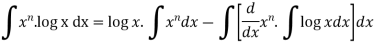
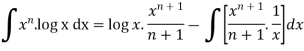
On solving, we get-

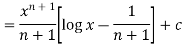
Q9) Explain simple integration.

A9)

Some standard form of simple integration-

If dy = f’(x) dx, then

If dy = a [f’(x) dx] where a is constant, then

If

, then

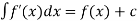
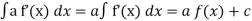
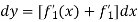
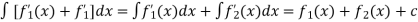
The integration of 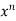will be as follows-

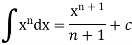
Q10) Write some fundamental integrals.

A10)