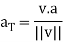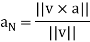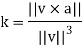Unit - 4

Triple product

Q1) What is the vector valued function?

A1)

The twisted cubic defined by the equations in (3) is the set of points of the form (t, 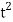, 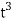) for real values of t . If we view each of these points as a terminal point for a vector r whose initial point is at the origin,

r = 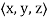= =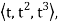ti+

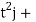
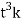
Then we obtain r as a function of the parameter t , that is, r = r(t). Since this function produces a vector, we say that r = r(t) defines r as a vector-valued function of a real variable, or more simply, a vector-valued function. The vectors that we will consider in this text are either in 2-space or 3-space, so we will say that a vector-valued function is in 2-space or in 3-space according to the kind of vectors that it produces.

If r(t) is a vector-valued function in 3-space, then for each allowable value of t the vector

r = r(t) can be represented in terms of components as

r = r(t) = 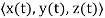= 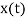i+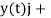

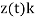
The functions x(t), y(t), and z(t) are called the component functions or the components of r(t).

Q2) Component functions of r(t) = 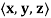= ti+ 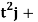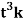are x(t) = t, y(t) = 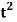, z(t) =

A2)

The domain of a vector-valued function r(t) is the set of allowable values for t. If r(t) is defined in terms of component functions and the domain is not specified explicitly, then it will be understood that the domain is the intersection of the natural domains of the component functions; this is called the natural domain of r(t).

Q3) Find the natural domain of

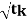
A3)

The natural domains of the component functions

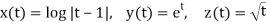
Are

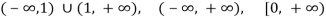
Respectively. The intersection of these sets is

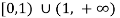
(verify), so the natural domain of r(t) consists of all values of t such that

0 ≤ t <1 or t > 1

Q4) Describe the graph of the vector-valued function r(t) = 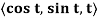= cos t i + sin t j + tk

A4)

The corresponding parametric equations are

x = cos t, y = sin t, z = t

The graph is a circular helix wrapped around a cylinder of radius 1.

Up to now we have considered parametric curves to be paths traced by moving points.

However, if a parametric curve is viewed as the graph of a vector-valued function, then we can also imagine the graph to be traced by the tip of a moving vector. For example, if the curve C in 3-space is the graph of

r(t) = x(t)i + y(t)j + z(t)k

And if we position r(t) so its initial point is at the origin, then its terminal point will fall on the curve C (as shown in Figure).

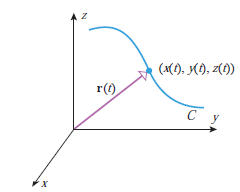
Thus, when r(t) is positioned with its initial point at the origin, its terminal point will trace out the curve C as the parameter t varies, in which case we call r(t) the radius vector or the position vector for C. For simplicity, we will sometimes let the dependence on t be understood and write r rather than r(t) for a radius vector.

Q5) Sketch the graph and a radius vector of r(t) = cos t i + sin t j, 0 ≤ t ≤ 2π

A5)

The corresponding parametric equations are x = cos t, y = sint (0 ≤ t ≤ 2π) so the graph is a circle of radius 1, centered at the origin, and oriented counterclockwise.

The graph and a radius vector are shown in Figure

Q6) What do you understand by the continuity of a vector-valued function?

A6)

Continuity:

We define a vector-valued function r(t) to be continuous at t = a if

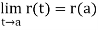
That is, r(a) is defined, the limit of r(t) as t→a exists, and the two are equal. As in the case for real-valued functions, we say that r(t) is continuous on an interval I if it is continuous at each point of I [with the understanding that at an endpoint in I the two-sided limit in (3) is replaced by the appropriate one-sided limit]. It follows that a vector-valued function is continuous at t = a if and only if its component functions are continuous at t = a.

Q7) If r(t) is a vector-valued function, then r is differentiable at t if and only if each of its component functions is differentiable at t, in which case the component functions of r’(t) are the derivatives of the corresponding component functions of r(t).

A7)

Assume that r(t) = x(t)i + y(t)j. Then

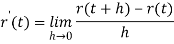
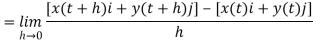
Q8) Find parametric equations of the tangent line to the circular helix

x = cos t, y = sin t, z = t

Where t = t0, and use that result to find parametric equations for the tangent line at the point where t = π.

A8)

The vector equation of the helix is

r(t) = cos t i + sin t j + tk

So we have

r0 = r(t0) = cos t0i + sin t0 j + t0k

v0 = r_

(t0) = (−sin t0)i + cos t0 j + k

It follows that the vector equation of the tangent line at t = t0 is

r = cos t0i + sin t0 j + t0k + t [(−sin t0)i + cos t0 j + k]

= (cos t0 − t sin t0)i + (sin t0 + t cos t0)j + (t0 + t)k

Thus, the parametric equations of the tangent line at t = t0 are

x = cos t0 − t sin t0, y= sin t0 + t cos t0, z= t0 + t

In particular, the tangent line at t = π has parametric equations

x = −1, y= −t, z = π + t

Q9) If r(t) is a differentiable vector-valued function in 2-space or

r(t). r’(t) = 0 that is, r(t) and r’(t) are orthogonal vectors for all t .3-space and r(t) is constant for all t, then

A9)

It follows that r1(t) = r2(t) = r(t)

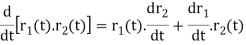
Or, equivalently,

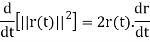
But 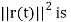constant so its derivative is zero. Thus

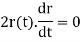
Q10) What is the definite integral of vector-valued function?

A10)

If r(t) is a vector-valued function that is continuous on the interval a ≤ t ≤ b, then we define the definite integral of r(t) over this interval as a limit of Riemann sums, except here the integrand is a vector-valued function. Specifically, we define

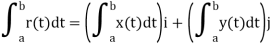
Or

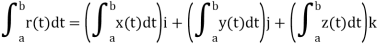
Q11) Find r(t) given that r’(t) = 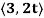and r(1) =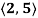

A11)

Integrating r’(t) to obtain r(t) yields

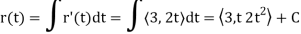
So that C = 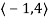. Thus,

r(t) = <3t, t2 >+< -1, 4> =< 3t – 1, t2 + 4>

Q12) A particle moves along a circular path in such a way that its x- and y-coordinates at time t are

x = 2 cos t, y = 2 sin t

Find the instantaneous velocity and speed of the particle at time t.

A12)

At time t , the position vector is

r(t) = 2 cos t i + 2 sin t j

So the instantaneous velocity and speed are

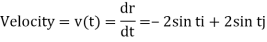
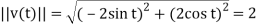
Q13) Particle moves through 3-space in such a way that its velocity is

v(t) = i + t j + k

Find the coordinates of the particle at time t = 1 given that the particle is at the point (−1, 2, 4) at time t = 0

A13)

Integrating the velocity function to obtain the position function yields

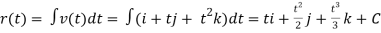… (1)

Where C is a vector constant of integration. Since the coordinates of the particle at time

t = 0 are (−1, 2, 4), the position vector at time t = 0 is

r(0) = −i + 2j + 4k   … (2)

It follows on substituting t = 0 in (1) and equating the result with (2) that

C = −i + 2j + 4k

Substituting this value of C in (1) and simplifying yields

r(t) = (t – 1)i + ( t2/2 + 2) j + (t3/3 + 4) k

Thus, at time t = 1 the position vector of the particle is

r(1) = 0i + 5/2 j + 13/3 k

So its coordinates at that instant are- (0, 5/2, 13/3)

Q14) Write a short note on tangent and normal components of acceleration.

A14)

If a particle moves along a smooth curve C in 2-space or 3-space, then at each point on the curve velocity and acceleration vectors can be written as

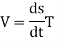
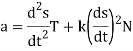
Where s is an arc length parameter for the curve, and T, N, and κ denote the unit tangent vector, unit normal vector, and curvature at the point

The coefficients of T and N are commonly denoted by

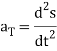
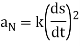
Which is written as-

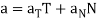
In this formula the scalars aT and aN are called the tangential scalar component of acceleration and the normal scalar component of acceleration, and the vectors 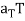and 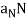are called the tangential vector component of acceleration and the normal vector component of acceleration.

Theorem: If a particle moves along a smooth curve C in 2-space or 3-space, then at each point on the curve the velocity v and the acceleration a are related to 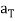, , 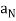and κ by the formulas