Unit - 1
Sets
Q1) What is the significance of discrete mathematics?
A1)
Computer science is all about the study of problems and solving problems by some process. The main goal is to develop an algorithm (a step by step list of some instructions in order to solve a certain problem).
According to K.H Rosen, discreet mathematics has more than one purpose but more importantly it equips computer science students with logical and mathematical skills.
By B.Miller and D. Ranum, A computing machine end is to develop an algorithm, a measure by step list of instructions in work outing a job. Algorithm are finite procedures that if followed will work out the job.
Discreet mathematics is the study of mathematics which deals on discreet structures like graphs, trees and networks.
It deals with discreet objects like integers and rational numbers which are separated from each other
Discreet mathematics is the language of computer science
The field of mathematics that are considered to be part of discrete mathematics include graph theory and the theory of computation. Topics in number theory such as congruence’s and recurrence relations are also considered part of discrete mathematics.
Q2) Define sets.
A2)
A set is a collection of well-defined objects which are called the elements or members of the set.
We generally use capital letters to denote sets and lowercase letters for elements.
If any element which exists in the set is to be denoted as-
Suppose an element ‘a’ is from a set X, then it is represented as- a
X
Which means the element ‘a’ belongs to the set X.
If the element is not form the group then we use ‘not belongs to’.
Q3) What do you understand by the proper sub-set and super set?
A3)
A set X is called proper subset the set Y is-
1. X is subset of Y
2. Y is not subset of X
Note- every set is a subset to itself.
If X and Y are two sets such that every element of X is an element of Y and every element of Y is an element of X, the set and set Y will be equal always.
We write it as X = Y and read as X and Y are identical.
Super set-
If X is a subset of Y, then Y is called a super set of X.
Q4) Prove that if ∅ and ∅’ are empty sets then ∅=∅’.
A4)
Let ∅≠ ∅’ then the following conditions must be true-
1. There is element x∈∅ such that x∉∅’
2. There is element x∈∅’ such that x∉∅.
But both these conditions are false since ∅’ and ∅’ has any elements if follows that ∅=∅’.
Q5) What do you understand by the cardinality of sets?
A5)
If A is finite set with n distinct elements, then n is called the cardinality of A. The cardinality of A is denoted by |A| [or by n (A)].
Example: Let A = {a, b, c, d}, then A is a finite set and |A| = 4
Cardinality of union of two sets-
Number of elements in A ∪B: (Cardinality of union) If A and B are any two finite sets then, the numbers of elements in A ∪B, denoted by | A ∪B | is given by | A ∪B | = | A | + | B | −| A ∩B |
Q6) What is the principle of inclusion an exclusion?
A6)
Let we have A and B are finite sets. Then A ∪B and A ∩B are
Finite and
n(A ∪B) = n(A) + n(B) −n(A ∩B)
That is, we find the number of elements in A or B (or both) by first adding n(A) and n(B) (inclusion) and then
Subtracting n(A ∩B) (exclusion) since its elements were counted twice
For three sets-
n(A ∪B ∪C) = n(A) + n(B) + n(C) −n(A ∩B) −n(A ∩C) −n(B ∩C) + n(A ∩B ∩C)
Q7) Define ordered pair.
A7)
An ordered pair of element a and b, where a is designated as the first element and b as the second element, it is denoted by (a, b).
In particular
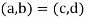
If and only if a = c and b = d. Thus
Unless a = b.
Q8) What do you understand by n-tuple?
A8)
A finite sequence over a set A is a function from {1, 2,….,n} into A, and it is usually denoted by
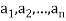
Such a sequence which is finite is called an n-tuple.
Here ‘n’ is a non-negative integer.
Tuples are written by listing the elements with parentheses ().
Q9) If A, B, C are sets then prove that-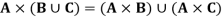 
A9)
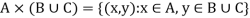
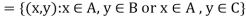
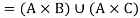
Q10) Define the Cartesian product of n-sets.
A10)
Let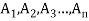 
denote n sets where n ≥2 , then the Cartesian product 
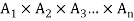is the set ofall n-tuples of the form 
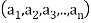where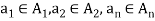 
From the definition we have
Q11) Define relation.
A11)
We define a relation in terms of ordered pairs-
An ordered pair of elements of x and y, where x is the first element and y is the second element, it is denoted by (x, y),
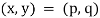
If and only if x = p and y = q
Thus (x, y)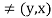
unless x = y
Relation-
Let X and Y are two sets, A relation from X to Y is a subset of 
.
Now suppose R is a relation form X to Y, then R is a set of ordered pairs where each first element comes from X and each second element comes from Y.
For each pair 
, one the following rule is true-
1. 
2.
The domain of a relation R is the set of all first elements of the ordered pairs which belongs to R, and range is the second element.
Q12) What do you understand by the composition of relations?
A12)
Let X, Y and Z are three sets and R be a relation from X to Y and S is a relation from Y to Z.
So that R is a subset of 
and S is a subset of 
.
Then R and S give a relation form X to Z which is denoted by RoS,
And can be defined as follows-
The relation RoS is called the composition of R and S.
Note- If R is a relation on a set A, that is, R is a relation from a set A to itself. Then the composition of R is RoR. Denoted by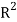 
.
Q13) Define symmetric and anti-symmetric relation.
A13)
A relation R on a set X is said to be symmetric if whenever xRy then yRx, that is if whenever (x, y)∈R then (y, x)∈R
R is said to be anti-symmetric if (x, y)∈X such that (x, y)∈R but (y, x)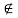
R
Q14) Let Z denote the set of integers and the relation R in Z be defined by “aRb” iff a – b is an even integer”. Then show that R is an equivalence relation.
A14)
1. R is reflexive; since
∅ = a −a is even, hence aRa for every a∈Z.
2. R is symmetric:
If a – b is even then b – a = – (a – b) is also even hence aRb⇒bRa
3. R is transitive: for if aRb and bRc then both a – b and b – c are even.
Consequently, a – c = (a – b) + (b – c) is also even.
∴aRb and bRc⇒aR c
Thus, R is an equivalence relation.
Q15) Let Z denote the set of integers and the relation R in Z be defined by “aRb” iff a – b is an even integer”. Then show that R is an equivalence relation.
A15)
1. R is reflexive; since
∅ = a −a is even, hence aRa for every a∈Z.
2. R is symmetric:
If a – b is even then b – a = – (a – b) is also even hence aRb⇒bRa
3. R is transitive: for if aRb and bRc then both a – b and b – c are even.
Consequently, a – c = (a – b) + (b – c) is also even.
∴aRb and bRc⇒aR c
Thus, R is an equivalence relation.
Q16) What is transitive closure of relations?
A16)
Let R be a relation on the set A. 
denote the transitive extension of R, 
denote the transitive extension of 
and in general 
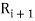denote the transitive extension of 
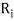then the transitive closure of R is defined as the set union of R, 
,
,
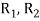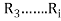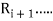It is denoted by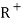 
Thus
Q17) Define partial ordering.
A17)
A relation R on a set Sis called a partial order relation in Sif R is, Reflexive Anti-symmetric and transitive.
A set S together with a partial ordering R is called a partially ordered set.
We denote a partial order relation by the symbol ≤.
Q18) Find the number of ways to partition of 10 peoples into four groups 
So that two teams contain 3 persons and two teams contain 2 persons.
A18)
By using above theorem, we get-
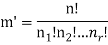
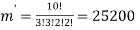ordered partitions
Here the group form an unordered partition so that we divide m’ by 
Because of the two cells with three elements each and 
Because of the two cells with two elements each.
So that-
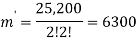
Q19) What is Injective function (One-To-One Mapping)?
A19)
A mapping 
is said to be one-to-one mapping if distinct elements of X are mapped into distinct elements of Y.
That means if f is a one-to-one mapping, then-
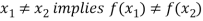
Or
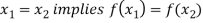
Q20) Prove that 
is both one-one and onto then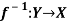 
is both one-one and onto.
A20)
Let f: X→Y be both one-one and onto.
Then there exist elements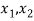 
∈X, and elements
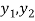∈Y
Such that
f(
) = 
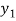, and f (
) =
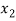Or
= 
(
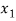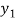) and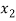 
= 
(
)
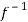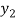Now,
Let 
(
) =
(
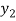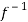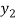), then
(
) =
(
)
⇒
= 
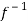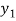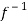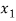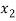
⇒f(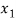
) = f (
)
⇒
= 
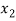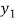Thus 
is one-one
Since f is onto, for y ∈ Y, there is some element x ∈ X, such that f (x) = y.
Now
f(x) = y
⇒x=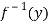 
So that 
is onto.
Hence 
is both one-one and onto.
Q21) Show that the inverse of an invertible mapping is unique.
A21)
Let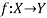 
By any invertible mapping,
Let,
g: Y→X
h: Y→X
Are two different inverse mapping of f.
Let y ∈ Y and
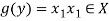
Now-
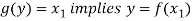
And
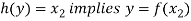
So that-
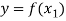and
Now-
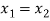
Which shows that g(y) = h(y)∀ y ∈ Y
So that the inverse of f is unique.
Q22) Prove that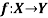 
is both one-one and onto then 
is both one-one and onto.
A22)
Let f: X→Y be both one-one and onto.
Then there exist elements 
∈X, and elements
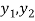∈Y
Such that
f(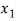
) = 
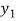, and f (
) =
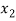Or
= 
(
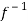) and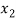 
= 
(
)
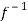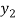Now,
Let 
(
) =
(
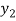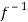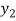), then
(
) =
(
)
⇒
= 
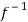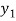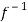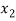
⇒f(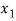
) = f (
)
⇒
= 
Thus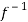 
is one-one
Since f is onto, for y∈Y, there is some element x∈X, such that f (x) = y.
Now
f(x) = y
⇒x= 
So that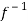 
is onto.
Hence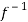 
is both one-one and onto.
Q23) Show that the inverse of an invertible mapping is unique.
A23)
Let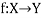 
By any invertible mapping,
Let,
g: Y→X
h: Y→X
Are two different inverse mapping of f.
Let y ∈ Y and
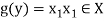
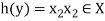
Now-
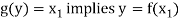
And
So that-
and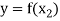
Now-
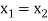
Which shows that g(y) = h(y)∀ y ∈ Y
So that the inverse of f is unique.
Q24) Show that addition is primitive recursive.
A24)
Addition is defined by a + 0 = a, a + (b + 1) = (a + b) + 1 for all natural numbers a a, b.
We define f (a, b) = a + b such that
f (a, b + 1) = a + b + 1 = (a + b) + 1
= f (a, b) + 1
= S (f (a, b))
Also f (a, 0) = a
We define f (a, b) as
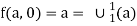
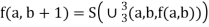
If follows that f comes from primitive recursion from 
and 
so that f is primitive recursive.
Q25) f: R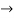 
R is defined by f (x) = a x + b, where a, b, x 
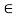R and a 
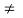0.
Show that f is invertible and find the inverse of f.
A25)
Firstly, we shall show that f is one-to-one.
Let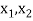 
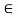R such that f (
) = f (
)
a x1 + b = ax2 + b
ax1 = ax2
x1 = x2
Thus f is one-one
To show that f is onto
Let y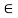 
R such that y = f (x)
y = ax + b
ax = y - b
i.e., given y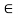 
R , there exists an element
x = 1/a (y – b) ∈ R, such that f(x) = y
This proves that f is onto
Hence f is one-one and onto
Hence f is invertible and
f-1(y) = 1/a (y – b)
Q26) Define statement.
A26)
When a declarative sentence which is true or false but not both is called statement
The truth values “true” and “false” of a statement are denoted by T ad F respectively. We can denote them by 0 and 1 as well.
Examples of statements are-
1. 2 + 11 = 12
2. Jaipur is in India
Compound statement (preposition):
Many propositions are composite, that is, composed of subpropositions and various connectives discussed subsequently. Such composite propositions are called compound propositions.
A proposition is said to be primitive if it cannot be broken down into simpler propositions, that is, if it is not composite.
For example, the above propositions (i) through (iv) are primitive propositions. On the other hand, the following two propositions are composite:
“Roses are red and violets are blue.” and “Vinay is smart or he studies every night.”
Statements can be connected by words like ‘not’, ‘and’, etc.
These words are known as logical connectives. The statements which do not contain any of the connectives are called atomic statements or simple statements.
The common connectives used are: negation (~) [or (￢)], and (∧) or (∨), if ... Then (→), if and only if (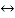
), equivalence (≡) or (⇔). We will use these connectives along with symbols to combine various simple statements.
Q27) What do you understand by direct proof?
A27)
A direct proof of p ⇒ q is a logically valid argument that begins with the assumptions that p is true and, in one or more applications of the law of detachment, concludes that q must be true.
So, to construct a direct proof of p ⇒ q, we start by assuming that p is true. Then, in one or more steps of the form p ⇒ q1, q1⇒ q2, ……., qn ⇒ q, we conclude that q is true.
Q28) Give a direct proof of the statement ‘The product of two odd integers is odd’.
A28)
Let us clearly analyse what our hypotheses are, and what we have to prove.
We start by considering any two odd integers x and y. So our hypothesis is p: x and y are odd.
The conclusion we want to reach is
q : xy is odd.
Let us first prove that p ⇒ q.
Since x is odd, x = 2m + 1 for some integer m.
Similarly, y = 2n + 1 for some integer n.
Then xy = (2m + 1) (2n + 1) = 2(2mn + m + n) +1
Therefore, xy is odd.
So we have shown that p ⇒ q.
Now we can apply modus ponens to p ∧ ( p ⇒ q) to get the required conclusion.
Q29) Give a direct proof of the theorem ‘The square of an even integer is an even integer.’
A29)
First of all, let us write the given statement symbolically, as
(∀ x ∈ Z)(p(x) ⇒ q(x))
Where p(x): x is even, and
q(x): x2 is even, i.e., q(x) is the same as p (x2 ).
The direct proof, then goes as follows.
Let x be an even number (i.e., we assume p(x) is true).
Then x = 2n, for some integer n (we apply the definition of an even number).
Then x2 = (2n)2 = 4n2 = 2(2n2).
x2 is even (i.e., q (x) is true).
Q30) Prove that ‘If x, y ∈ Z such that xy is odd, then both x and y are odd.’, by proving its contrapositive.
A31)
Let us name the statements involved as below.
p : xy is odd
q : both x and y are odd.
So,
~ p : xy is even, and
~ q : x is even or y is even, or both are even.
We want to prove p ⇒ q, by proving that ~ q ⇒ ~ p. So we start by assuming that ~ q is true, i.e., we suppose that x is even.
The x = 2n for some n ∈ N.
Therefore, xy = 2ny.
Therefore xy is even, by definition.
That is, ~ p is true.
So, we have shown that ~ q ⇒ ~p. Therefore, p ⇒ q.
Q31) Pradeep will get good marks if and only if he studies regularly means that Pradeep will get good marks if he studies regularly and Pradeep studies regularly if he gets good marks.
A32)
Truth table for two-way implication-
p | q | p q | q p | p ↔ q |
T T F F | T F T F | T F T T | T T F T | T F F T |
Q32) What is compound proposition?
A33)
Many propositions are composite, that is, composed of sub-propositions and various connectives discussed
Subsequently such composite propositions are called compound Propositions. A proposition is said to be primitive if it cannot be broken down into simpler propositions, that is, if it is not composite.
Following two propositions are composite:
“Roses are red and violets are blue.” and “John is smart or he studies every night.”
Q33) Explain division algorithm.
A34)
Let a and b be integers with b 
0. Then there exists integers q and r such that
a = bq + r and 0 ≤ r < |b|
Also, the integers q and r are unique.
The number q in the above theorem is called the quotient, and r is called the remainder. We stress the fact that r must be non-negative. The theorem also states that r = a – bq
Division Algorithm using a Calculator:
Suppose a and b are both positive. Then one can find the quotient q and remainder r using a calculator as follows:
Step 1. Divide a by b using the calculator, that is, find a/b.
Step 2. Let q be the integer part of a/b, that is, let q = INT (a/b).
Step 3. Let r be the difference between a and bq, that is, let r = a − bq.
Q34) What is divisibility?
A35)
Let a and b be integers with a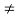 
0. Suppose ac = b for some integer c. We then say that a divides b or b is divisible by a, and we denote this by writing
a | b
We also say that b is a multiple of a or that a is a factor or divisor of b. If a does not divide b, we will write a ∤ b
Note-
Suppose a, b, c are integers.
(i) If a | b and b | c, then a | c.
(ii) If a | b then, for any integer x, a | bx.
(iii) If a | b and a | c, then a | (b + c) and a|(b − c).
(iv) If a | b and b 
0, then a =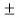 
b or |a| < |b|.
(v) If a | b and b | a, then |a| = |b|, i.e., a =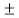 
b.
(vi) If a | 1, then a =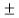 
1
Q35) What do you understand by Euclidean algorithm?
A36)
Let a and b be integers, and let d = gcd(a, b). One can always find d by listing all the divisors of a and then all the divisors of b and then choosing the largest common divisor. The complexity of such an algorithm is f (n) = 0(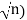
where n = |a| + |b|. Also, we have given no method to find the integers x and y such that
d = ax + by.
This subsection gives a very efficient algorithm, called the Euclidean algorithm, with complexity f (n) = O(log n), for finding d = gcd(a, b) by applying the division algorithm to a and b and then repeatedly applying it to each new quotient and remainder until obtaining a nonzero remainder. The last nonzero remainder is d = gcd(a, b).
Then we give an “unraveling” algorithm which reverses the steps in the Euclidean algorithm to find the integers x and y such that d = xa + yb.
Q36) What is Chinese remainder theorem?
A37)
Once a Chinese riddle asks the following question-
Is there a positive integer x such that when x is divided by 3 it yields a remainder 2, when x is divided by 5 it yields a remainder 4, and when x is divided by 7 it yields a remainder 6?
In other words, we seek a common solution of the following three congruence equations:
x ≡ 2 (mod 3), x ≡ 4 (mod 5), x ≡ 6 (mod 7)
Theorem (Chinese remainder theorem):
Consider the system
x ≡ r1 (mod 
), x ≡ r2 (mod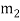 
), ・ ・ ・, x≡
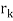(mod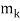 
)
Where the mi are pairwise relatively prime. Then the system has a unique solution modulo M =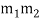 
・ ・
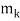
Q37) State and prove Fermat’s little theorem.
A38)
Let a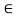 
N and let p be a prime-
1. If p does not divide a then 
≡ (mod p).
2. In general,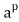
≡ a (mod p).
Proof:
Suppose p is any prime number and a is any integer such that p ∤ a. Note that a _= 0 because otherwise p would divide a. Consider the set of integers
S = {a, 2a, 3a, . . . , (p − 1)a}.
We claim that no two elements of S are congruent modulo p. For suppose sa ≡ ra (mod p) for some integers s and r with 1 ≤ r < s ≤ p − 1. Then, by definition of congruence modulo p,
p | (sa − ra), or, equivalently, p | (s − r )a.
Now p ∤ a by hypothesis, and because p is prime, gcd(a, p) = 1. Thus, by Euclid’s lemma, p | (s − r ). But this is impossible because 0 < s − r < p.
Consider the function F from S to the set T = {1, 2, 3, . . . , (p − 1)} that sends each element of S to its residue modulo p. Then F is one-to-one because no two elements of S are congruent modulo p.
If a function from one finite set to another is one-to-one, then it is also onto. Hence F is onto, and so the p − 1 residues of the p − 1 elements of S are exactly the numbers
1, 2, 3, . . . , (p − 1).
It follows that
a ·2a ·3a · · · (p − 1)a ≡ [1·2·3 · · · (p − 1)] (mod p),
Or equivalently
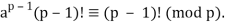
But because p is prime, p and (p − 1)! are relatively prime. Thus, by the cancellation theorem for modular congruence
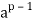≡ (mod p)
