Unit - 3
Matrices
Q1) Define matrices.
A1)
A matrix is a rectangular arrangement of the numbers.
These numbers inside the matrix are known as elements of the matrix.
A matrix ‘A’ is expressed as-
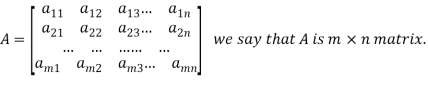
The vertical elements are called columns and the horizontal elements are rows of the matrix.
The order of matrix A is m by n or (m× n)
Q2) What is triangular matrix? How many types of there of triangular matrix?
A2)
Triangular matrix-
If every element above or below the leading diagonal of a square matrix is zero, then the matrix is known as a triangular matrix.
There are two types of triangular matrices-
(a) Lower triangular matrix-
If all the elements below the leading diagonal of a square matrix are zero, then it is called lower triangular matrix.
Example:
A = 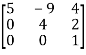
(b) Upper triangular matrix-
If all the elements above the leading diagonal of a square matrix are zero, then it is called lower triangular matrix.
Example-
A = 
Q3) What is transpose of a matrix?
A3)
Transpose of a matrix: The matrix obtained from any given matrix A , by interchanging rows and columns is called the transpose of A and is denoted by 
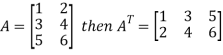
The transpose of matrix  Also
Also 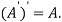
Note: 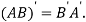
Q4) Check whether the following matrix A is symmetric or not?
A = 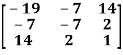
A4)
As we know that if the transpose of the given matrix is same as the matrix itself then the matrix is called symmetric matrix.
So that, first we will find its transpose,
Transpose of matrix A,
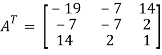
Here,
A = 
So that, the matrix A is symmetric.
Q5) Show that any square matrix can be expressed as the sum of symmetric matrix and anti- symmetric matrix.
A5)
Suppose A is any square matrix
Then,
A = 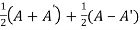
Now,
(A + A’)’ = A’ + A
A+A’ is a symmetric matrix.
Also,
(A - A’)’ = A’ – A
Here A’ – A is an anti – symmetric matrix
So that,
Square matrix = symmetric matrix + anti-symmetric matrix
Q6) Express the matrix A as sum of Hermitian and skew-Hermitian matrix where 
A6)
Let A =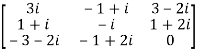
Therefore 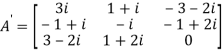 and
and 
Let 
Again 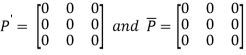
Hence P is a Hermitian matrix.
Let 
Again 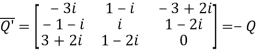
Hence Q is a skew- Hermitian matrix.
We Check
P +Q=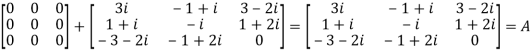
Hence proved.
Q7) Find the minors and cofactors of the first row of the determinant.

A7)
(1) The minor of element 2 will be,
Delete the corresponding row and column of element 2,
We get,
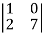
Which is equivalent to, 1 × 7 - 0 × 2 = 7 – 0 = 7
Similarly the minor of element 3 will be,
4× 7 - 0× 6 = 28 – 0 = 28
Minor of element 5,
4 × 2 - 1× 6 = 8 – 6 = 2
The cofactors of 2, 3 and 5 will be,
(-1)1+1(7) = +7
(-1)1+2(28) = - 28
(-1)1+3(2) = +2
Q8) Show that,
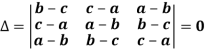
A8)
Applying
C1 C1 + C2 + C3
We get,
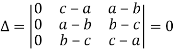
Q9) Solve-
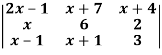
A9)
Given-
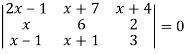
Apply- 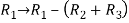
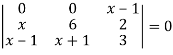
We get-
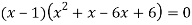

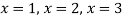
Q10) Show that the points given below are collinear-
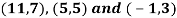
A10)
First we need to find the area of these points and if the area is zero then we can say that these are collinear points-
So that-
We know that area enclosed by three points-

Apply- 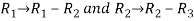
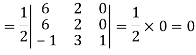
So that these points are collinear
Q11) Find the inverse of matrix ‘A’ if-

A11)
Here we have-
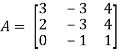
And the matrix formed by its co-factors of |A| is-
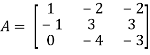
And
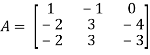
Therefore-
We know that-
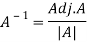
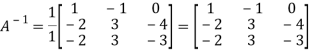
Q12) Find the inverse of matrix ‘A’ by using elementary transformation-
A = 
A12)
Write the matrix ‘A’ as-
A = IA
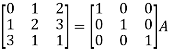
Apply  , we get
, we get
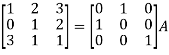
Apply 
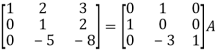
Apply 
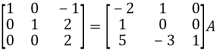
Apply 
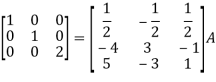
Apply 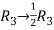
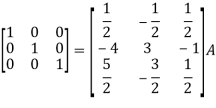
So that,
 =
= 
Q13) Find the inverse of the matrix  by row transformation?
by row transformation?
A13)
Let A=
By Gauss-Jordan method
We have 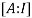
=
Apply 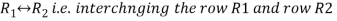

Apply  we get
we get

Apply  we get
we get
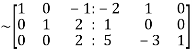
Apply 
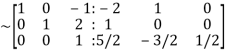
Apply 
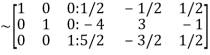
Hence 
Q14) Find the inverse of the matrix  by row transformation?
by row transformation?
A14)
Let A= 
By Gauss-Jordan method
We have 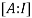
=
Apply  we get
we get
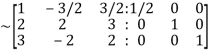
Apply 
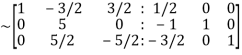
Apply 
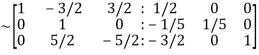
Apply 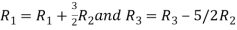
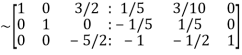
Apply 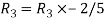
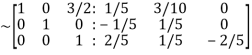
Apply 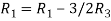
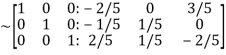
Hence 
Q15) Find the rank of a matrix M by echelon form.
M = 
A15)
First we will convert the matrix M into echelon form,
M = 
Apply,  , we get
, we get
M = 
Apply 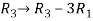 , we get
, we get
M = 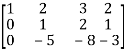
Apply 
M = 
We can see that, in this echelon form of matrix, the number of non – zero rows is 3.
So that the rank of matrix X will be 3.
Q16) Find the rank of a matrix A by echelon form.
A = 
A16)
Convert the matrix A into echelon form,
A = 
Apply 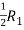
A = 
Apply  , we get
, we get
A = 
Apply  , we get
, we get
A = 
Apply  ,
,
A = 
Apply 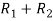 ,
,
A = 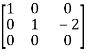
Therefore the rank of the matrix will be 2.
Q17) State and prove rank-nullity theorem.
A17)
Let A is a matrix of order m by n, then-

Proof: If rank (A) = n, then the only solution to Ax = 0 is the trivial solution x = 0by using invertible matrix.
So that in this case null-space (A) = {0}, so nullity (A) = 0.
Now suppose rank (A) = r < n, in this case there are n – r > 0 free variable in the solution to Ax = 0.
Let  represent these free variables and let
represent these free variables and let 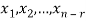 denote the solution obtained by sequentially setting each free variable to 1 and the remaining free variables to zero.
denote the solution obtained by sequentially setting each free variable to 1 and the remaining free variables to zero.
Here  is linearly independent.
is linearly independent.
Moreover every solution is to Ax = 0 is a linear combination of 
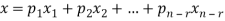
Which shows that  spans null-space (A).
spans null-space (A).
Thus  is a basis for null-space(A) and nullity (A) = n – r.
is a basis for null-space(A) and nullity (A) = n – r.
Q18) Find the solution of the following homogeneous system of linear equations
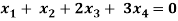
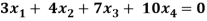

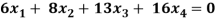
A18)
The given system of linear equations can be written in the form of matrix as follows,
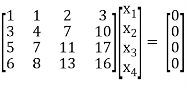
Apply the elementary row transformation,
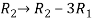
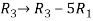
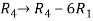 , we get,
, we get,
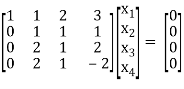
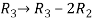
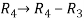 , we get
, we get
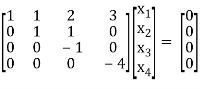
Here r(A) = 4, so that it has trivial solution,
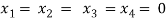
Q19) Check whether the following system of linear equations is consistent of not.
2x + 6y = -11
6x + 20y – 6z = -3
6y – 18z = -1
A19)
Write the above system of linear equations in augmented matrix form,
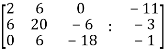
Apply 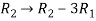 , we get
, we get
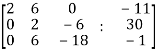
Apply 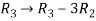
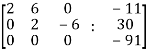
Here the rank of C is 3 and the rank of A is 2
Therefore both ranks are not equal. So that the given system of linear equations is not consistent.
Q20) Solve the following system of equations by gauss-jordan method
 +
+ 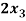 - 2
- 2 = 0
= 0
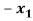 +
+ 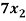 +
+ 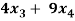 = 0
= 0
 - 7
- 7 +
+  = 0
= 0
A20)
The given system of equations can be written in the form of matrices as follows,
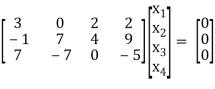
By applying operation - we get,
we get,
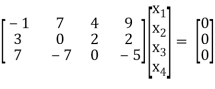
Now apply, 
We get,
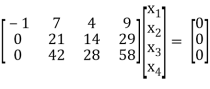
Apply, 
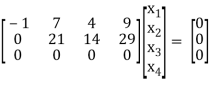
The set of the equations we get from above matrices,
 +
+ 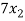 +
+ 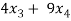 = 0 …………………..(1)
= 0 …………………..(1)
21 +
+  = 0 …………………………..(2)
= 0 …………………………..(2)
Suppose 
From equation-2, we get
21
Now from equation-1:
- (
( ) + 4b + 9a = 0
) + 4b + 9a = 0
We get,
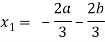

Q21) Find the characteristic equation and characteristic roots of the matrix A:
A = 
A21)
We know that the characteristic equation of the matrix A will be-
| = 0
= 0
So that matrix A becomes,
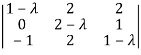 = 0
= 0
Which gives , on solving
(1-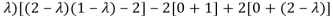 = 0
= 0
Or 
Or (
Which is the characteristic equation of matrix A.
The characteristic roots will be,
(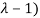 (
(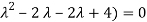
(
(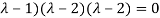
Values of  are-
are-
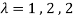
These are the characteristic roots of matrix A.
Q22) Find the sum and the product of the Eigen values of  ?
?
A22)
The sum of Eigen values = the sum of the diagonal elements
 =1+(-1)=0
=1+(-1)=0
The product of the Eigen values is the determinant of the matrix
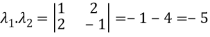
On solving above equations we get 
Q23) Find out the Eigen values and Eigen vectors of  ?
?
A23)
The Characteristics equation is given by 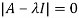
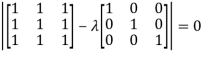

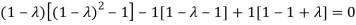
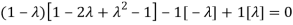
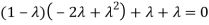
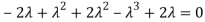
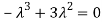
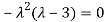
Or 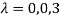
Hence the Eigen values are 0,0 and 3.
The Eigen vector corresponding to Eigen value  is
is
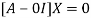
Where X is the column matrix of order 3 i.e.

This implies that 
Here number of unknowns are 3 and number of equation is 1.
Hence we have (3-1) = 2 linearly independent solutions.
Let 
Thus the Eigen vectors corresponding to the Eigen value  are (-1,1,0) and (-2,1,1).
are (-1,1,0) and (-2,1,1).
The Eigen vector corresponding to Eigen value 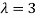 is
is
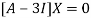
Where X is the column matrix of order 3 i.e.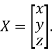

This implies that 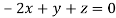
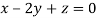
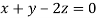
Taking last two equations we get
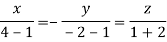
Or 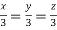
Thus the Eigen vectors corresponding to the Eigen value  are (3,3,3).
are (3,3,3).
Hence the three Eigen vectors obtained are (-1,1,0), (-2,1,1) and (3,3,3).
Q24) Find out the Eigen values and Eigen vectors of 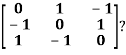
A24)
Let A =
The characteristics equation of A is  .
.
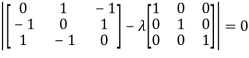
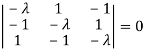
Or 
Or 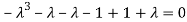
Or 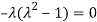
Or 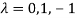
The Eigen vector corresponding to Eigen value 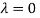 is
is
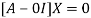
Where X is the column matrix of order 3 i.e.

Or 
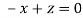
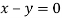
On solving we get 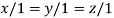
Thus the Eigen vectors corresponding to the Eigen value  is (1,1,1).
is (1,1,1).
The Eigen vector corresponding to Eigen value 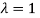 is
is
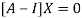
Where X is the column matrix of order 3 i.e.
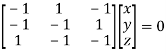
Or 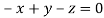


On solving  or
or  .
.
Thus the Eigen vectors corresponding to the Eigen value  is (0,0,2).
is (0,0,2).
The Eigen vector corresponding to Eigen value 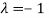 is
is
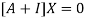
Where X is the column matrix of order 3 i.e.
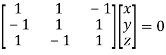
Or 
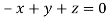

On solving we get 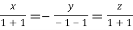 or
or  .
.
Thus the Eigen vectors corresponding to the Eigen value  is (2,2,2).
is (2,2,2).
Hence three Eigen vectors are (1,1,1), (0,0,2) and (2,2,2).