Unit - 2
Introduction to compartmental models
Q1) What are compartmental models?
A1)
Compartmental model provides a means to formulate models for processes which have inputs and/or outputs over time. In this chapter, we will study modelling of radioactive decay processes, pollution levels in lake systems and the absorption of drugs into the bloodstream, exponential growth model, density dependent growth, limited growth harvesting using compartmental techniques.
Definition: Compartmental Model is a model in which there is a place called compartment which has amount of substance in and amount of substance out over time.
Q2) What is balance law?
A2)
Statement: The rate of change of quantity of substance is equal to ‘Rate in’minus ‘Rate out’ of the compartment.
Symbolically, if X(t) is the amount of quantity in the compartment, then
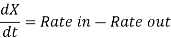
Compartmental Diagram:

Word Equation:
In words, balance law can be written as:
{Net rate of change of a substance} = {Rate in} – {Rate out}
This Equation is known as “word equation” of the model.
Q3) Explain exponential decay radioactivity.
A3)
Radioactive elements are those elements which are not stable and emit αparticles, β- particles or photons while decaying into isotopes of other elements. Exponential decay model for radioactive decay can be considered as a compartmental model with compartment being the radioactive material with no input but output as decay of radioactive sample over time.

Fig.: Input – output compartmental diagram for radioactive nuclei
Word equation:
By Balance Law, word equation can be written as
{Rate of change of radioactive material at time t} = {Rate amount of radioactive material decayed}
Q4) What are the assumptions of radioactive decay model?
A4)
1. Amount of an element present is large enough so that we are justified in ignoring random fluctuations.
2. The process is continuous in time.
3. We assume a fixed rate of decay for an element.
4. There is no increase in mass of the body of material
Q5) Give the solution of differential equation of Exponential Decay Model.
A5)
We have
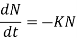
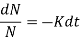
Integrating both sides, we get
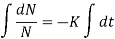
Ln N =-Kt + In C , where C is the constant of integration.
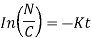
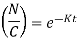
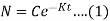
Put initial condition, N(0) = i.e., at t = 0, N =
i.e., at t = 0, N = 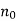 we get
we get
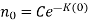
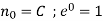
Put C = 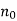 in equation (1) we get
in equation (1) we get  where K is the constant of proportionality. Moreover the value of K depends on the particular radioactive material.
where K is the constant of proportionality. Moreover the value of K depends on the particular radioactive material.
Q6) Explain lake pollution model.
A6)
Balance Law in Lake Pollution Model: There is an input of polluted water from the river flowing into the lake, or due to a pollution dump into the lake, and an output as water flows from lake carrying some pollution with it. This gives the word equation as follows:
Word Equation:
(rate of change of pollution in lake} = {pollution in} – {pollution out}
Compartmental Model of Lake Pollution:
Assumption of lake pollution model: The lake has a constant volume V and that it is continuously well mixed so that the pollution is uniform throughout.
Let x(t) = Amount of pollutant in the lake at time t.
V = Volume of the lake.
V1 = Volume of water flowing in and out of the lake.
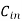 = Concentration of pollution of incoming water.
= Concentration of pollution of incoming water.
Since volume of lake is constant,
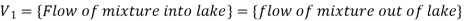
By Balance Law, rate of change of pollution = Pollution in – Pollution out
That implies:
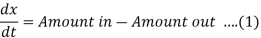
Also, Amount in = Concentration in × Volume =
Amount out = Concentration out × Volume = 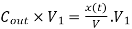
Because

Substituting the values of Amount in and Amount out in equation (i), we get
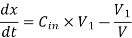
At initial condition, 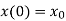
Therefore, the initial value problem is
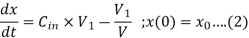
Let C = Concentration of pollutant in lake at any time t, then
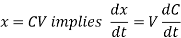
Then equation (ii) implies that
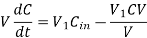
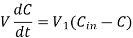

This is called the differential equation of the lake pollution model.
Q7) Suppose in a lake, the pollution level is 7%. If the concentration of incoming water is 2% and 10000 litres per day water is allowed to enter the lake, find time when pollution level is 5%. Volume of the lake is 200000 litres. Also, find pollution after 32 days.
A7)
Here given
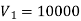
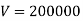
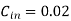


We find ‘t’
We know that
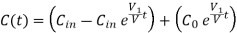
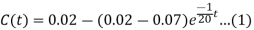
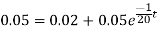
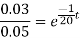
Taking log on both sides, we get
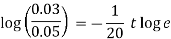
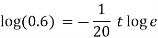
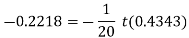

Therefore, at t = 10.214 days, pollution level is 5%.
Now, we take t = 32 and find C(t). Put t = 32 in (i)
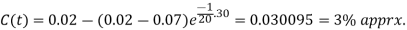
Q8) What is drug assimilation into the blood?
A8)
Drug Assimilation Model can be considered as a compartmental model with two compartments, corresponding to GI tract (gastrointestinal tract) and bloodstream. The GI tract compartment has a single input and output and the bloodstream compartment has a single input and output.
Compartmental diagram:

Fig: Input – output compartmental diagram for drug assimilation.
Word Equation: The application of balance law gives the following two word equations, one for each compartment.
{Rate of change of drug in GI tract} = {Rate of drug intake} – {Rate drug leaves GI tract}
And
{Rate of change of drug in blood} = {Rate drug enters blood} – {Rate drug leaves blood}
Q9) What are the assumptions for the population growth model?
A9)
Assumptions for the Population Growth Model:
1. Population is sufficiently large so that we ignore random differences between individuals.
2. The births and deaths are continuous in time.
3. We assume that per capita birth and death rates are constant in time.
4. An individual is not making any impact on population.
Q10 Give the procedure to formulate the differential equation of population growth model.
A10)
Let x(t) be the population at time t
𝑥0 = initial population
α = constant per capita death rate per individual per unit of time.
β = constant per capita birth rate per individual per unit of time. Rate of change of population at any time t is directly proportional to the size of population at that time therefore, dx/dt αx
Rate of deaths = α x(t)
Rate of births = β x(t)
By Balance Law,
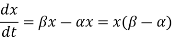
Let r = β - α , r is the growth rate for the population.
Clearly, r > 0 in exponential growth.
At initial condition, population is x(0) = x0 Hence initial value problem corresponding to exponential growth model is given by
Q10) Give the expression of solution of exponential growth model.
A11)
Here we have
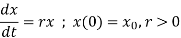
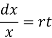
Integrate both sides,
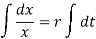
Log x ln , c = + rt c where is the constant of integration.
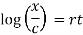
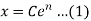
At initial condition, x(0) = x0. So, put x = x0 at t = 0 in (i), we get
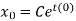
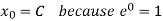
Put C = 𝑥0 in equation (i) we get,
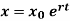
Q11) How do we formulate the differential equation for density dependent model.
A12)
Formulating the differential equation
Let x(t) be the population at time t
x0 = initial population α = constant per capita death rate due to normal deaths.
β = constant per capita birth rate
γx = per capita death rate due to density dependent deaths. It is assumed to be proportional to population size.
K = Carrying capacity for population. It is defined as the population size for which per capita birth rate equals per capita death rate.
Since, we assume that rate of change of population at time t is directly proportional to the size of population at that time, therefore

So, overall birth rate is the product of per capita birth rate and the current population size. Therefore,
Rate of births = β x(t)= β x
Also, overall birth rate is the product of per capita death rate and the current population size. Therefore, Rate of deaths = α x(t)= α x
Death due to crowding is per capita death rate due to density multiplied by current population size. Therefore,
Rate of deaths due to density = 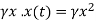
Then by Balance Law,
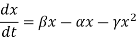
Let r = β − α , then
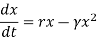
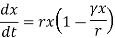
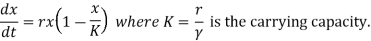
At initial condition, x(0) = x0 .Therefore, equation for density dependent growth model is :
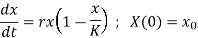
It is also known as Limited growth of population model or Logistic equation.
Q12) In a population, the initial population is 100. Suppose the population can be modelled using the differential equation  with a time step of one month. Find predicted population after 2 months.
with a time step of one month. Find predicted population after 2 months.
A13)
The given differential equation is
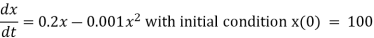
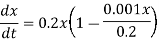
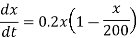
It is of the form
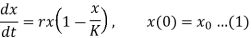
Such that r = 0.2 , K = 200 ,x0 = 100.
We know that the solution of limited growth of population model given by (i) is
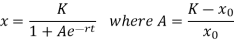
Here
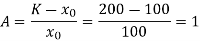
Therefore, the solution of the given system is,
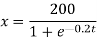
Now, at t = 2 months,
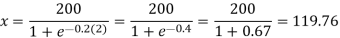
Hence the population after 2 months is 119.76.
Q13) Let N(t) be the number of professors who adopted the technology, then  where M is the total population of professors. It is assumed that rate of adoption is proportional to both the number who adopted technology and fraction who did not adopted technology. If M = 10000, a = 0.5, initially 100 professors adopted professors, find time for 80% of professors to adopt technology.
where M is the total population of professors. It is assumed that rate of adoption is proportional to both the number who adopted technology and fraction who did not adopted technology. If M = 10000, a = 0.5, initially 100 professors adopted professors, find time for 80% of professors to adopt technology.
A14)
Here given
We are given that N = 80% of M = 80/100 * 10000 = 8000
Also N(0) = 100, M = 10000, a = 0.5. We find t.
Also,
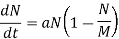
It is of the form

Where x = N = 8000, r = a = 0.5, x0 = N(0) = 100, K = M = 10000.
The solution of (i) is
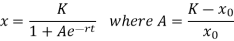
Here
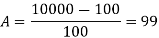
Therefore, the solution of the given system is
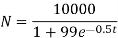
Put N = 8000, we get
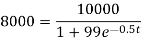
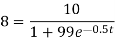
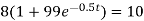
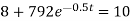

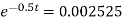
Take log on both sides we get
− = 0.5 t loge = log(0.002525)
⇒ − = 0.5 t(0.4343) = -2.5977
t=11.96 or 12 approx.
After 12 units of time, 80% population adopted technology.
Q14) What do you understand by limited growth with harvesting?
A15)
The effect of harvesting a population on a constant basis is of paramount importance in many industries such as fishing industry. This model is useful in answering the questions like “Will a high harvesting rate destroy the population? Or Will a low harvesting rate destroy the viability of the industry. Limited population growth model with harvesting is a compartmental model with compartment being the world, there is an input of population through births and an output through deaths.
Word equation: By Balance Law, word equation can be written as
{ rate of change in pop.} = {rate of births} – {normal rate of deaths} – {rate of deaths by crowding or density} – {Rate of death by harvesting}
Assumptions for the Density Dependent Growth Model
1. Population is sufficiently large so that we can ignore random differences between individuals.
2. The births and deaths are continuous in time.
3. We assume that per capita birth and death rates are constant in time.
4. We ignore immigration and emigration.
5. We account for increased death rate due to competition of limited resources and the fact that population stabilizes after a long period.
6. We assume increased deaths due to harvesting.
Q15) How do we formulate differential equation limited population growth model with harvesting
A16)
Let x(t) be the population at time t
𝑥0 = initial population
α = constant per capita death rate.
β = constant per capita birth rate
r = per capita reproduction rate or growth rate = β - α
γ x = per capita death rate due to density.
K = Carrying capacity for population.
h= constant rate of harvesting i.e., deaths due to harvesting per unit time.
Since, we assume that rate of change of population at time t is directly proportional to the size of population at that time, therefore
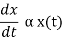
Rate of births = β x(t)= βx
Rate of normal deaths = α x(t)= α x
Rate of deaths due to density = 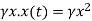
Rate of deaths due to harvesting = h
Then by Balance Law,
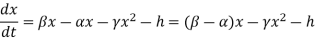
Let r = β - α, then
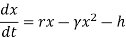
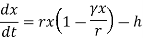
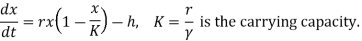
At initial condition, x(0) = x0 .Therefore, equation for limited population growth model with harvesting is:
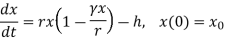
Q16) In a fish farm, fish are harvested at a constant rate of 2100 fish per week. The per capita death rate for the fish is 0.2 fish per day per fish and per capita birth rate is 0.7 fish per day per fish. (a) Write down a word equation and differential equation for rate of change of fish population. (b) Find when the fish population is in equilibrium. (c) If initial fish population is 700, find fish population after a week.
A17)
We are given that h = 2100fish per week = 2100/7 = 300 fish per day. Also α = 0.2, β = 0.7
Word equation: By Balance Law, word equation can be written as
{ rate of change in pop.} = {rate of births} – {normal rate of deaths} – {rate of deaths by crowding or density} – {Rate of death by harvesting}
Differential equation:
Let x(t) be the fish population at any time t.
α = constant per capita death rate.
β = constant per capita birth rate
h= constant rate of harvesting i.e., deaths due to harvesting per unit time.
Then differential equation is:
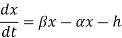
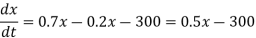

(b) At equilibrium,
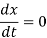
⇒ 0.5x -300 = 0
⇒ x = 600
Therefore, at x = 600 fishes, fish population is in equilibrium.
(c) We have
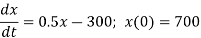
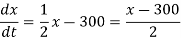
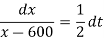
Integrating both sides, we get
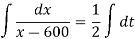
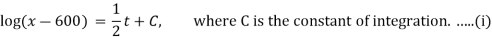
Put x(0) = 700, we get
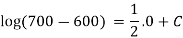
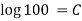
Put the value of C in (i), we get
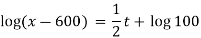
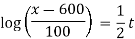
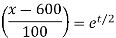
When t = 7, we have
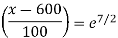
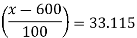
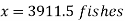
After a week, fish population is 3912 fishes approximately.