Unit - 2
Sequences and Subsequences
Q1) Define sequence.
A1)
A function f: N 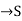 , where S is a non-empty set, is called sequence, for each nϵN.
, where S is a non-empty set, is called sequence, for each nϵN.
The sequence is written as f(1) , f(2) , f(3) , f(4)……….f(n).
Any sequence f(n) can be denoted as <f(n)> or {f(n)} or (f(n)).
Suppose f(n) = 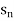
Then it can be written as - 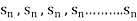 and can be denoted as <
and can be denoted as <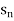 >or {
>or {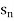 } or (
} or (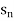 )
)
 is the n’th term of the sequence.
is the n’th term of the sequence.
Q2) What are finite and infinite sequences?
A2)
1. Finite sequence- A sequence which has finite number of terms is called finite sequence.
2. Infinite sequence- A sequence which is not finite , called infinite sequence.
Q3) Define sub-sequences.
A3)
Given a sequence {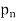 }, consider a sequence {
}, consider a sequence {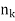 } of positive integers such that
} of positive integers such that  <
<  <
<  . . . Then the sequence {
. . . Then the sequence {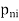 } is called a subsequence of {
} is called a subsequence of {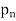 }. If {
}. If {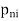 } converges its limit is called a subsequential limit of {
} converges its limit is called a subsequential limit of {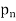 }.
}.
It is clear that {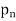 } converges to p if and only if every subsequence of {
} converges to p if and only if every subsequence of { } converges to p.
} converges to p.
Q4) What are bounded above and bounded below sequences?
A4)
Bounded above sequence: A sequence {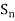 } is said to be bounded above if there exists a number K such that,
} is said to be bounded above if there exists a number K such that,

Bounded below sequence: A sequence { } is said to be bounded below if there exists a number K such that,
} is said to be bounded below if there exists a number K such that,

Q5) Define convergent and divergent sequences.
A5)
Convergent sequence- A sequence Sn is said to be convergent when it tends to a finite limit. That means the limit of a sequence Sn will be always finite in case of convergent sequence.
Divergent sequence- when a sequence tends to ±∞ then it is called divergent sequence.
Q6) consider a sequence 2, 3/2 , 4/3 , 5/4, …….. Here Sn = 1 + 1/n
A6)
According to def.
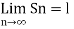
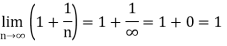
Q7) Define limit of a sequence.
A7)
A sequence <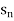 > is said to tend to limit “l”, when given any positive number ‘ϵ’ , however small , we can always find a integer ‘m’ such that |
> is said to tend to limit “l”, when given any positive number ‘ϵ’ , however small , we can always find a integer ‘m’ such that |  – l| <ϵ , for every for all, n≥m , and we can define this as follows,
– l| <ϵ , for every for all, n≥m , and we can define this as follows,
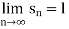
Q8) Prove that A convergent sequence of real numbers is bounded
A8)
Suppose that lim 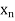 = x and let e := 1. Then there exists a natural number
= x and let e := 1. Then there exists a natural number
K = K(1) such that |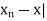 < 1 for all n
< 1 for all n 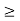 K. If we apply the Triangle Inequality with
K. If we apply the Triangle Inequality with
n 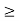 K we obtain
K we obtain 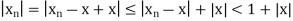
If we set

Then it follows that |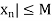 for all
for all 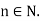
Q9) Prove that If X =(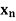 ) is a convergent sequence of real numbers and if
) is a convergent sequence of real numbers and if 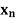
 0 for all n
0 for all n 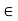 N, then x = lim(
N, then x = lim(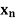 )
)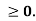
A9)
Suppose the conclusion is not true and that x < 0; then e:= -x is positive. Since X converges to x, there is a natural number K such that
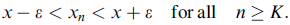
In particular, we have 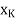 < x + e = x + (-x) = 0. But this contradicts the hypothesis that
< x + e = x + (-x) = 0. But this contradicts the hypothesis that 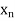
 0 for all n
0 for all n 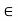 N. Therefore, this contradiction implies that x
N. Therefore, this contradiction implies that x 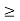 0.
0.
Q10) Define monotonic sequence.
A10)
A sequence  is said to be monotonic increasing if
is said to be monotonic increasing if  and monotonic decreasing if
and monotonic decreasing if 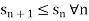 .
.
It is said to be monotonic if it is either increasing or decreasing.
A sequence 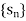 is strictly increasing if
is strictly increasing if 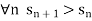 and strictly decreasing if
and strictly decreasing if 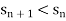 .
.
Here note that the monotonic sequences never oscillate. They either converge of diverge.
Q11) Prove that Every monotonic increasing sequence which is not bounded above, diverges to +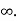
A11)
Let 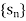 be a monotonic increasing sequence, not bounded above. Let G be any number however large.
be a monotonic increasing sequence, not bounded above. Let G be any number however large.
Since the sequence is unbounded and monotonic increasing,  a positive integer m such that
a positive integer m such that
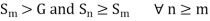

Hence,
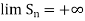
Q12) Show that the sequence 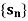 where
where

A12)
Here
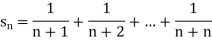
Now
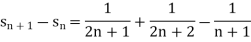
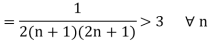
Hence the sequence is monotonic increasing.
Again
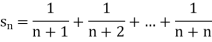
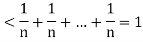
Which means- 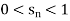
The sequence is bounded.
Hence the sequence, being bounded and monotonic increasing, is convergent.
Q13) What is the divergence criteria?
A13)
If a sequence X = (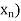 of real numbers has either of the following properties, then X is divergent.
of real numbers has either of the following properties, then X is divergent.
(i) X has two convergent subsequences X’ = 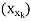 and
and 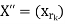 whose limits are not equal.
whose limits are not equal.
(ii) X is unbounded.
Q14) State and prove Bolzano-Weierstrass theorem.
A14)
Statement- Every sequence has a limit point.
Proof:
Let 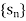 be a bounded sequence and S = {
be a bounded sequence and S = { be its range.
be its range.
Since the sequence is bounded, therefore its range set S is also bounded.
There are two possibilities:
- S is finite
- S is infinite
Now take first case- If S is finite then there must exist at least one member 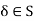 , such that
, such that 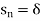 for an infinite number of values of n. This means that every neighbourhood,
for an infinite number of values of n. This means that every neighbourhood, 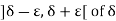 contains
contains 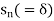 for an infinite number of values of n.
for an infinite number of values of n.
Thus 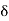 is a point of the sequence
is a point of the sequence 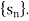
Case-2: When S is infinite, since it is bounded. It has by Bolzano-Weierstrass theorem, at least one limit point (say 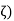
Again, since 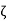 is a limit point of S therefore every neighbourhood
is a limit point of S therefore every neighbourhood  contains an infinity of members of S.
contains an infinity of members of S.
Which means 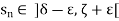 for an infinity of values of n. Hence
for an infinity of values of n. Hence 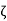 is a limit point of the sequence.
is a limit point of the sequence.
Note- the converse of the theorem is not true, for there do exist unbounded sequences having only one real limit point.
Q15) What is Cauchy’s sequence?
A15)
A sequence {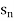 } in a metric space (X, d) is said to be a Cauchy sequence if for every
} in a metric space (X, d) is said to be a Cauchy sequence if for every 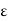 > 0 there is an integer N such that d(
> 0 there is an integer N such that d(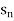 ,
,  ) <
) < 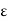 for all n, m
for all n, m 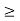 N.
N.
Definition:
Let E be a non-empty subset of a metric space (X, d), and let S = {d(p, q) : p, q 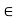 E}. The diameter of E is sup S.
E}. The diameter of E is sup S.
If {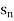 } is a sequence in X and if En consists of the points
} is a sequence in X and if En consists of the points 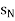 ,
,  , . . ., it is clear that {
, . . ., it is clear that {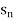 } is a Cauchy sequence if and only if
} is a Cauchy sequence if and only if
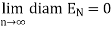
Q16) Explain the Cauchy’s sequence of uniform convergence.
A16)
The necessary and sufficient condition for a sequence of functions (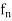 ) defined on A to converge uniformly on A is that for every
) defined on A to converge uniformly on A is that for every 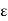 > 0, there exists a positive integer m such that
> 0, there exists a positive integer m such that
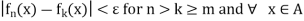
Proof: Condition is necessary. It is given that (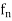 ) is uniformly convergent on A.
) is uniformly convergent on A.
Let 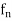 – f uniformly on A. Then given
– f uniformly on A. Then given 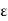 > 0, there exists a positive integer m such that
> 0, there exists a positive integer m such that
 and
and 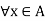
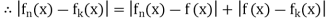
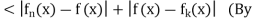 triangular inequality)
triangular inequality)
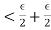 for n>k
for n>k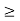 m and
m and  This proves the necessary part. Now we prove the sufficient part.
This proves the necessary part. Now we prove the sufficient part.
Condition is sufficient: It is given that for every  > 0, there exists a positive integer m such that
> 0, there exists a positive integer m such that
| (x) –
(x) – 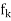 (x)| <
(x)| < 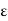 for n > k m and for all x in A. But by Cauchy’s principle of convergence of sequence of real numbers, for each fixed point x of A, the sequence of numbers (
for n > k m and for all x in A. But by Cauchy’s principle of convergence of sequence of real numbers, for each fixed point x of A, the sequence of numbers (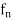 (x)) converges.
(x)) converges.
In other words, (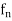 ) is pointwise convergent say to f on A. Now for each
) is pointwise convergent say to f on A. Now for each 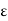 > 0, there exists a positive integer m such that
> 0, there exists a positive integer m such that
|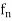 (x) –
(x) – 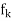 (x)| <
(x)| <  for n>k
for n>k
Fix k and let n ® ¥. Then 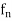 (x) ® f(x) and we get
(x) ® f(x) and we get
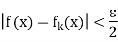
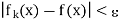
This is true for k 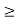 m and for all x in A. This shows that (f) is uniformly convergent to f on A, which proves the sufficient part.
m and for all x in A. This shows that (f) is uniformly convergent to f on A, which proves the sufficient part.
Q17) check whether the series 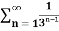 is convergent or divergent. Find its value in case of convergent.
is convergent or divergent. Find its value in case of convergent.
A17)
The general formula for this series is given by,
Sn = 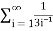 =
= 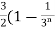 )
)
We get,
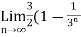 ) = 3/2
) = 3/2
Hence the series is convergent and its values is 3/2.
Q18) check whether the following series is convergent or divergent. If convergent, find its value.
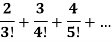
A18)
n’th term of the series will be,
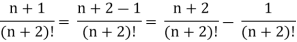
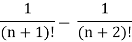
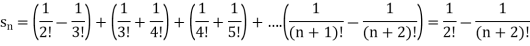

Q19) Prove that a Cauchy sequence of real numbers is bounded.
A19)
Let X = ( be a Cauchy sequence and let
be a Cauchy sequence and let 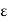 := 1. If H := H(1) and n
:= 1. If H := H(1) and n 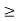 H, then |
H, then |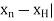 < 1. Hence, by the Triangle Inequality, we have |
< 1. Hence, by the Triangle Inequality, we have |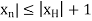 for all
for all
n  H. If we set
H. If we set
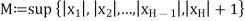
Then it follows that | M for all n
M for all n 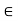 N.
N.
Cauchy Convergence Criterion A sequence of real numbers is convergent if and only if it is a Cauchy sequence
We have seen, above in Lemma, that a convergent sequence is a Cauchy sequence.
Conversely, let X = (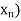 be a Cauchy sequence; we will show that X is convergent to some real number. First we observe from Lemma that the sequence X is bounded.
be a Cauchy sequence; we will show that X is convergent to some real number. First we observe from Lemma that the sequence X is bounded.
Therefore, by the Bolzano-Weierstrass Theorem, there is a subsequence X’ = (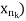 of X that converges to some real number x.
of X that converges to some real number x.
We shall complete the proof by showing that X converges to 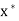 .
.
Since X = (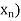 is a Cauchy sequence, given
is a Cauchy sequence, given 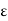 > 0 there is a natural number H(
> 0 there is a natural number H(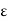 /2) such that if n, m
/2) such that if n, m 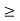 H(
H(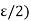 then
then
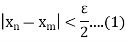
Since the subsequence X’= (
Converges to 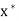 , there is a natural number K
, there is a natural number K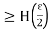
Belonging to the set {n1; n2; . . .} such that
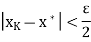
Since K 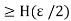 , it follows from (1) with m = K that
, it follows from (1) with m = K that
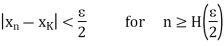
Therefore, if n 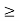
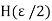 , we have
, we have
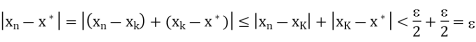
Sincee  > 0 is arbitrary, we infer that lim(
> 0 is arbitrary, we infer that lim( =
= 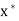 . Therefore the sequence X is
. Therefore the sequence X is
Convergent.
Q20) Test the convergence of the following series.
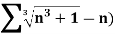
A20)
We have 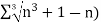
First we will find  and the
and the 
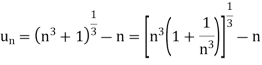
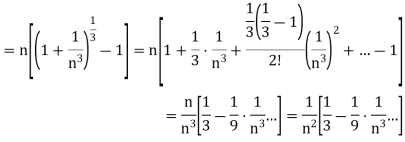
And
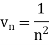

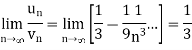
Here, we can see that, the limit is finite and not zero,
Therefore, 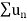 and
and 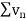 converges or diverges together.
converges or diverges together.
Since 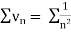 is of the form
is of the form 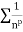 where p = 2>1
where p = 2>1
So that, we can say that,
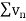 is convergent, so that
is convergent, so that 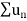 will also be convergent.
will also be convergent.
Q21) Test for the convergence of the n’th term of the series given below-
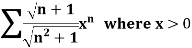
A21)
We have,


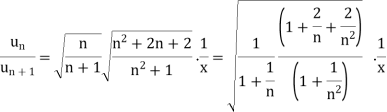
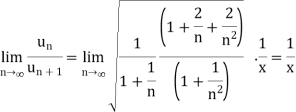
Now, by D’Almbert ratio test 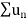 converges if
converges if 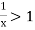 and diverges if
and diverges if 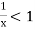
At x = 1, this test fails.
Now, when x = 1 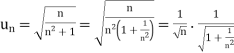
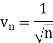
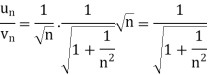
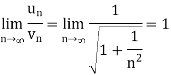
The limit is finite and not zero.
Then by comparison test, 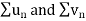 converges or diverges together.
converges or diverges together.
Since 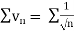 is the form of
is the form of 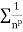 , in which
, in which 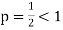
Hence 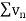 diverges then
diverges then 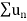 will also diverge.
will also diverge.
Therefore in the given series 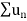 converges if x<1 and diverges if x≥1.
converges if x<1 and diverges if x≥1.
Q22) Test the convergence of the series whose nth term is given below-
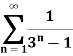
A22)


By root test  is convergent.
is convergent.
Q23) Test the convergence of the following series:
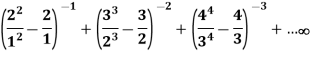
A23)
Here, we have, 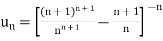
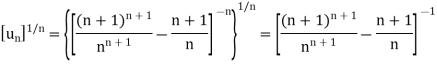
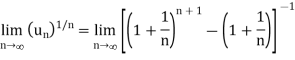
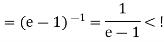
Therefore the given series is convergent.
Q24) Test the series for its convergence.
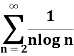
A24)
Let, f(x) = 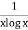
 =
= 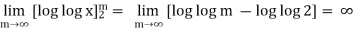
Here we notice that, by Cauchy’s integral test, the series is divergent.
Q25) Test the series by integral test-
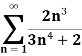
A25)
Here 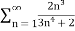 decreases as n increases and it is positive.
decreases as n increases and it is positive.
By using integral test,
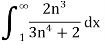
= 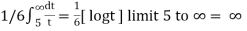
We get infinity,
So that the series is divergent.
Q26) Test the convergence of the following alternating series:

A16)
Here in the series, we have 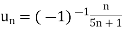
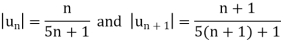
First condition-
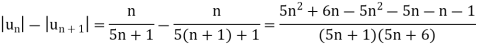
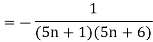
So that,
|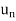 | > |
| > | |
|
That means, each term is not numerically less than its preceeding terms.
Now second condition- 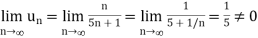
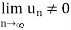
Both conditions are not satisfied for convergence.
Hence the given series is not convergent. It is oscillatory.
Q27) Test the convergence/Divergence of the series:
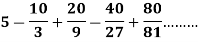
A27)
Here the given series is alternately negative and positive, which is also a geometric infinite series.
Suppose,
S = 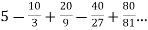
According to the conditions of geometric series,
Here, a = 5, and common ratio (r) = -2/3
Thus, we know that,
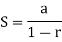
So,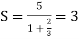
Sum of the series is finite, which is 3.
So we can say that the given series is convergent.
Now.
Again sum of the positive terms,

The series is geometric, then
A = 5 and r = 2/3 , then
Sum of the series,
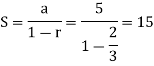
Sum of the series is finite then the series is convergent.
Both conditions are satisfied, then the given series is absolutely convergent.