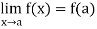Unit - 3

Limits of functions

Q1) Define limit of a function.

A1)

Let A 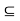R. A point c 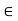R is a cluster point of A if for every 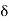> 0 there exists at least one point x 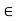A; x c such that |x - c| < .

We can define this in the language of neighborhoods as-

A point c is a cluster point of the set A if every d-neighborhood 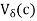  = (c- , c+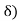 of c contains at least one point of A distinct from c.

For example, if A := {1, 2}, then the point 1 is not a cluster point of A, since choosing 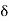:= 1 2 gives a neighborhood of 1 that contains no points of A distinct from 1. The same is true for the point 2, so we see that A has no cluster points

Q2) Define limit.

A2)

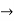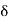Let A   R, and let c be a cluster point of A. For a function f : A R, a real number L is said to be a limit of f at c if, given any > 0, there exists a > 0 such that if x 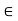A and 0 < |x - c| < , then |f(x) – L| <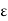

Note:

1. Since the value of 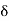usually depends on 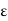, we will sometimes write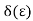instead of to emphasize this dependence.
2. The inequality 0 < |x - c| is equivalent to saying x c.

If L is a limit of f at c, then we also say that f converges to L at c. We often write

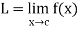or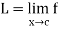

We also say that ‘‘f (x) approaches L as x approaches c.’’

If the limit of f at c does not exist, we say that f diverges at c.

Q3) Define Right Hand Limits and Left Hand Limits.

A3)

Let a function f be defined in a neighbourhood of a point ‘a’ except possibly at ‘a’. It is said to tend to a number A as x tends to a number ‘a’ from the right or through values greater than ‘a’ if given a number > 0, there exists a number 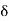  > 0 such that

|f(x) –A| < 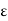  for a <x < a + .

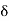We write, it as

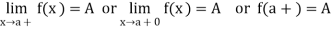
The function f is said to tend to a number A as x tends to ‘a’ from the left or through values smaller than ‘a’ if given a number E > 0, there exists a number 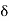  > 0 such that

|f(x) – A| < 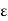  for a – 6 < x < a.

We write it as

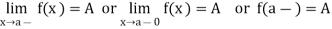
Q4) Find the limit of the function f defined by

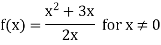
When x tends to zero.

A4)

The given function is not defined at x = 0 since f(0) =0/0 which is not defined or indeterminate form.

If x tends to 0, then f(x) = 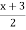. Therefore

Right Hand Limit =

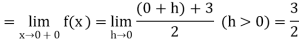
Left Hand Limit =

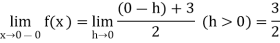
Since both the right hand and left hand limits exist and are equal,

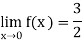
Q5) Define Algebraic Operations on Functions

A5)

Let f and g be two functions with domain D R. Then the sum, difference, product, quotient of f and g denoted by f + g, f – g, fg, f/g are functions with domain D defined by

(f + g) (x) = f(x) + g(x)

(f – g) (x) = f(x) – g(x)

(fg) (x) = f(x). g(x)

(f/g) (x) = f(x)/g(x)

Provided in the last case g(x)  0 for all x in D.

Q6) Prove that if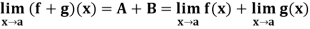

A6)

Since 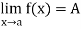and 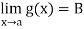, corresponding to a number There exist numbers

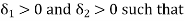
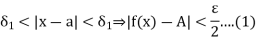
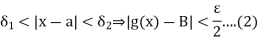
Let 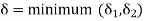Then from (1) and (2) we have that

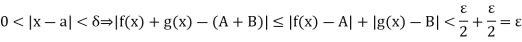
Which shows that

Q7) Prove that if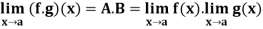

A7)

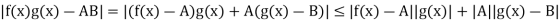…………(3)

Since 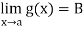corresponding to 1, there exists a number
such that

Which implies that |g(x) 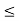|g(x) – B| + |B| 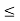1 + |B| = K (say) ………..(4)

Since f(x) = A, corresponding to   < 0, there exists a number 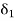> 0 such that number 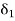< 0 such that

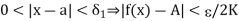…………(5)

Since 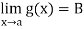corresponding to  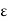 > 0, there exists a number > 0 such that

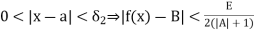……….(6)

Let 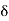= min (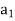, , 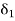). Then using (4), (5) and (6) in (3), we have for 0 < |x – a| < ,

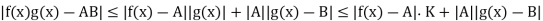
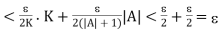…………..(7)

Therefore 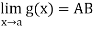it means

Q8) Find the following limit

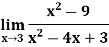
A8)

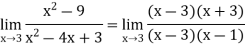
Hence

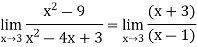
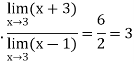
Q9) Evaluate-

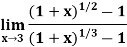
A9)

To make the problem easier, we make a substitution which enables us to get rid of fractional powers 1/2 and 1/3. L.C.M. Of 2 and 3 is 6. So, we put 1 + x =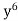

Then we have

Q10) What is continuous function?

A10)

Continuity of a Function at a Point

A function f defined on a subset S of the set R is said to be continuous at a point a S, if

Note that in this definition, we assume that S contains some open interval containing the point a.

If we assume that there exists a half open (semi-open) interval [a, c[ contained in S for some c R, then in the above definition, we can replace 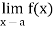by 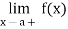say that the function is continuous from the right of a or f is right continuous at a.

Similarly, you can define left continuity at a, replacing the role of by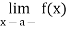

Thus, f is continuous from the right at a if and only if

It is continuous from the left at a if and only if

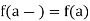
Q11) Examine the continuity of signum function.

A11)

The signum function, as we know a function f: R R defined as

f(x) = 1 if x > 0

= 0 if x = 0

= –1 if x < 0

This function is not continuous at the point x = 0. We have already seen that f(0+) = 1, f(0–) = –1.

Since f(0+) 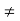f(0–), 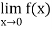i does not exist and consequently the function is not continuous at

x = 0. For every point x 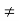0 the function f is continuous. This is easily seen from the graph of

The function f. There is a jump at the point x = 0 in the values of f(x) defined in a neighbourhood

Of 0.

Note that if f: R R is defined as,

f(x) = 1 if x 0.

= –1 if x < 0.

Then, it is easy to see that this function is continuous from the right at x = 0 but not from the left.

It is continuous at every point x 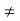0.

Similarly, if f is defined by f(x) = 1 if x > 0

= –1 if x 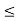0

Then f is continuous from the left at x = 0 but not from the right.

Q12) Discuss the continuity of the function sin x on the real line R.

A12)

Let f(x) = Sin x for every  x 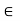R

We show by the (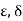)-definition that f is continuous at every point of R.

Consider an arbitrary point a R. We have

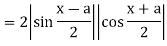
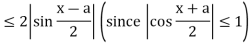
From Trigonometry, we know that

Therefore,

Consequently

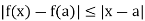< if |x-a| < δ  where δ= 

So f is continuous at the point a. But a is any point of R. Hence Sin x is continuous on the real line R.

Q13) What is sequential continuity.

A13)

Let f be a real-valued function whose domain is a subset of the set R. The function f is said to be continuous at a point a if, for every sequence (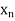) in the domain of f converging to a, we have,

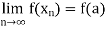
Q14) Let f: R 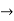R be defined as

Prove that f is continuous on R by using the sequential definition of the continuity of a function.

A14)

Suppose (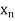) is a sequence which converges to a point ‘a’ of R. Then, we have

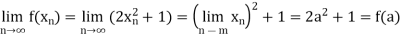
This shows that f is continuous at a point a belongs to R. Since a is an arbitrary element of R, therefore, f is continuous everywhere on R.

Q15) Let f and g be two real functions such that the range of g is contained in, the domain of f. If g is continuous at x = a, f is continuous at b = g(a) and h(x) = f(g(x)), for x in the domain of g, then h is continuous at a.

A15)

Given 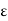> 0, the continuity of f at b = g(a) implies the existence of an 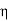> 0 such that for

Corresponding to 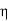  > 0, from the continuity of g at x = a, we get a  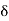 > 0 such that

  (2)

From (1) and (2) we get,

implies that

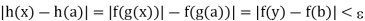
Where we have taken y = g(x). Hence h is continuous at a which proves the theorem.

Q16) Define non-continuous function.

A16)

A function f: S R fails to be continuous on its domain S if it is not continuous at a particular point of S. This means that there exists a point a S such that, either

(i)                does not exist, or

(ii) 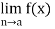             ) exists but is not equal to f(a).

But we know that a function f is continuous at a point a if and only if

f(a+) = f(a–) = f(a).

Thus, if f is not continuous at a, then one of the following will happen:

(i) Either f(a+) or f(a–) does not exist (this includes the case when both f(a+) and f(a) do not exist).

(ii) Both f(a+) and f(a–) exist but f(a+) f(a–).

(iii) Both f(a+) and f(a–) exist and f(a+) = f(a–) but they are not equal to f(a).

If a function f: S R is discontinuous for each b 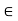S, then we say that totally discontinuous an S.

Q17) Prove that A function f continuous on a bounded and closed interval [a, b] is necessarily a bounded function.

A17)

Let S be the collection of all real numbers c in the interval [a, b] such that f is bounded on the interval [a, c]. That is, a real number c in [a, b] belongs to S if and only if there exists a constant such that |f(x)|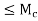 for all x in [a, c]. Clearly, S 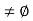since a S and b is an upper bound for S.

Hence, by completeness property of R, there exists a least upper bound for S. Let it be k (say).

Clearly, k b. We prove that k S and k = b which will complete the proof of the theorem.

Corresponding to = 1, by the continuity of f at k( b) there exists a d > 0 such tha

|f(x) – f(k)| < 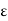  = 1 whenever |x – k| < d, x [a, b].

By the triangle inequality we have

|f(x)| – |f (k)|  |f(x) – f(k)| < 1

Hence, for all x in [a. b] for which |x – k| < d, we have that

|f(x)| < |f(k)| + 1     ...(1)

Since k is the least upper bound of S, k – d is not an upper bound of S. Therefore, there is a number

c 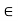S such that

k – d < c 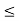k

Consider any t such that k 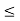t < k + d. If x belongs to the interval [c, t] then |x – k| < d. For,

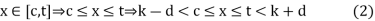
Now c 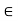S implies that there exists 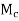> 0 such that for all

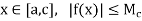
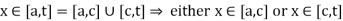
If x 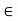[a, c], by (3) we have

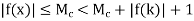
If, however, x [c, t] then by (1) and (2) we have

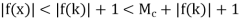
In any case we get that x [a, t] implies that

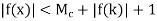
This shows that f is bounded in the interval [a, t] thus proving that t S whenever k  t < k + d.

In particular k S. In such a case k = b. For otherwise we can choose a ‘t’ such that k < t < k + d and

t S which will contradict the fact that k is an upper bound.

Q18) Show that the function f such that f(x) = x  for every x ]0, 1[ is continuous but does not attain its bounds.

A18)

As mentioned the identity function f is continuous in ]0, 1[. Here the domain of f is

Bounded but is not a closed interval. The function f is bounded with least upper bound (1.u.b) =

1 and greatest lower bound (g.l.b) = 0 and both the bounds are not attained by the function, since range of f = ]0, 1[.

Q19) State and prove Bolzano’s Intermediate Value Theorem.

A19)

Statement:

Let f be a continuous function on an interval containing a and b. If K is any number between f(a) and f(b) then there is a number c, a c S b such that f(c) = K.

Proof:

Either f(a) = f(b) or f(a) < f(b) or f(b) < f(a). If f(a) = f(b) then K = f(a) = f(b) and so c can be taken to be either a or b. We will assume that f(a) < f(b). (The other case can be dealt with similarly.) We can, therefore, assume that f(a) < K < f(b).

Let S denote the collection of all real numbers x in [a, b] such that f(x) < K. Clearly S contains a, so S 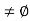and b is an upper bound for S. Hence, by completeness property of R, S has least upper bound and let us denote this least upper bound by c. Then a   c 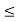  b. We want to show that f(c) = K.

Since f is continuous on [a, b], f is continuous at c. Therefore, given > 0, there exists a 6 > 0 such that whenever x is in [a, b] and |x – c| < 6, |f(x) – f(c) ( < G,

f(c) – 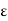  < f(x) < f(c) + 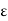. ………..(1)

If c b, we can clearly assume that c + 6 < b. Now c is the least upper bound of S. So c – is not

‘an upper bound’ of S. Hence, there exists a y in S such that c – 6 < y  c. Clearly |y – c| < 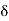  and so by (1) above, we have

Since y is in S, therefore f(y) < K. Thus, we get

f(c) – S < K

If now c = b then K – 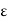  < K < f(b) = f(c), i.e., K < f(c) + E. If c 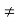b, then c < b; then there exists an x such that c < x < c + 6, 6, x 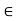[a, b] and for this x, f(x) < f(c) +  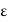 by (1) above. Since x > c, K 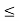f(x), for otherwise x would be in S which will imply that c is not an upper bound of S. Thus, again we have K 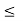f(x) < f(c) + E.

In any case,

K < f(c) + 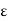……….(2)

We get for every 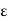  > 0

f (c) –   < K < f(c) +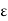

Which proves that K = f(c), since is arbitrary while K, f(c) are fixed. In fact, when f(a) < K < f(b) and f(c) = K, then a < c < b.

Q20) What is uniform Continuity of a Function?

A20)

Let f be a function defined on a subset A contained in the set R of all reals. If corresponding to any number > 0, there exists a number   > 0 (depending only on G) such that

Then we say that f is uniformly continuous on the subset A.

An immediate consequence of the definition of uniform continuity is that uniform continuity in a set A implies pointwise continuity in A.

Q21) Show that the function, f: R - R

Is uniformly continuous on R

A21)

Let 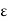  be any positive number. Let 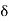> 0 be any arbitrary positive number. Choose

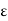x > /  and y = x + 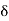/2. Then

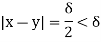
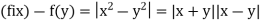
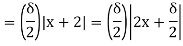
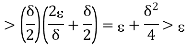
That is whatever 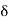  > 0 we choose, there exist real numbers x, y such that |x – y| <  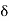 but |f(x) –

f(y)|> G which proves that f is not uniformly continuous.

Q22) State and prove Uniform Continuity Theorem.

A22)

Let I be a closed bounded interval and let f : I  R be continuous on I. Then f is uniformly continuous on I.

Proof:

If f is not uniformly continuous on I then, by the preceding result, there exists

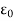> 0 and two sequences () and () in I such that |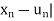 < 1/n and | 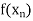 - f(| 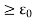for all n N. Since I is bounded, the sequence () is bounded; by the Bolzano- Weierstrass Theorem, here is a subsequence k of (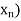 that converges to an element z. Since I is closed, the limit z belongs to I, by Theorem. It is clear that the corresponding subsequence 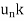Þalso converges to z, since

Now if f is continuous at the point z, then both of the sequences f(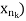 and f( 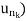must converge to f ðzÞ. But this is not possible since

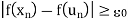
For all n N. Thus the hypothesis that f is not uniformly continuous on the closed bounded interval I implies that f is not continuous at some point z I. Consequently, if f is continuous at every point of I, then f is uniformly continuous on I.