Unit – 1
Symmetries of a square
Q1) What are rotational symmetries?
A1)
An equilateral triangle can be rotated by 120 degree, 240 degree, or 360 degree angles without changing it.
If we rotate the triangle by 31 degree or 87 degree we notice that the bottom edge of the triangle is no longer perfectly horizontal.
Many other shapes that are not regular polygons also have rotational symmetries.
Several shapes with rotational symmetries are given below

The first shape can be rotated any integer multiple of 72 degree.
We say that a shape has rotational symmetry of order n if it can be rotated by any multiple of 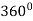 /n without changing its appearance. We can imagine constructing other shapes with rotational symmetries of arbitrary order. If the only rotations that leaves a shape unchanged are multiples of 360!, then we say that the shape has only the trivial (order n = 1) symmetry.
/n without changing its appearance. We can imagine constructing other shapes with rotational symmetries of arbitrary order. If the only rotations that leaves a shape unchanged are multiples of 360!, then we say that the shape has only the trivial (order n = 1) symmetry.
Q2) Explain the concept of symmetries of square.
A2)
A square is more symmetric than a triangle. Any two squares in the same row can be obtained from one another through rotations, whereas those in distinct rows can only be obtained from one another through a reflection.
If we remove a square region from a plane, move it in some way, then put the square back into the space it originally occupied.
Here we need to describe the possible relationships between the initial position of the square and its final position in terms of motions.
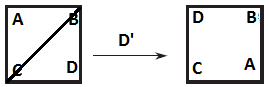
The final position of the square is completely determined by the location and orientation (that is, face up or face down) of any particular corner. But, clearly, there are only four locations and two orientations for a given corner, so there are exactly eight distinct final positions for the corner.
- Rotation of 0° (no change in position)
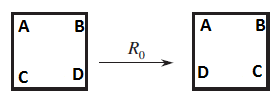
2. Rotation of 90° (counterclockwise)
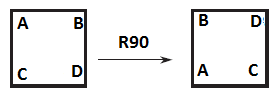
3. Rotation of 180°
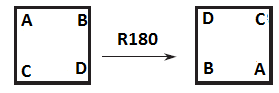
4. Rotation of 270°
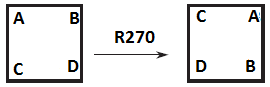
5. Flip about a horizontal axis
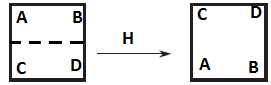
6. Flip about vertical axis

7. Flip about the main diagonal
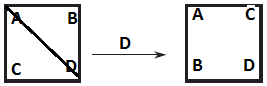
8. Flip about the other diagonal
Q3) Define Dihedral groups.
A3)
The dihedral group 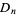 is the symmetry group of an
is the symmetry group of an  -sided regular polygon for
-sided regular polygon for 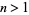 . The group order of
. The group order of 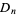 is
is 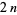 . Dihedral groups
. Dihedral groups 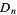 are non-Abelian permutation groups for
are non-Abelian permutation groups for 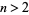 .
.
Note- The dihedral group of order 2n is often called the group of symmetries of a regular n-gon.
A symmetry group consisting of the rotational symmetries of  ,
, 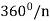 ,
, 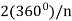 , . . . , (n-1)
, . . . , (n-1)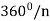 , and no other symmetries is called a cyclic rotation group of order n and is denoted by
, and no other symmetries is called a cyclic rotation group of order n and is denoted by 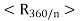 .
.
Q4) What is the cyclic index for Dihedral groups?
A4)
The cycle index (in variables 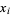 , ...,
, ..., 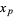 ) for the dihedral group
) for the dihedral group 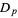 is given by
is given by
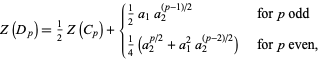 (1)
(1)
Where
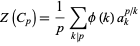
Is the cycle index for the cyclic group 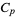 ,
, 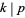 means
means 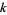 divides
divides 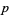 , and
, and 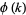 is the totient function. The cycle indices for the first few
is the totient function. The cycle indices for the first few 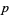 are
are
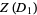

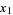 (3)
(3)
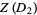

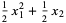 (4)
(4)
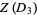

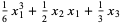 (5)
(5)
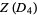

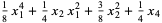 (6)
(6)
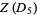

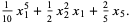
Q5) What do you understand by binary operations?
A5)
Let G be a set. A binary operation on G is a function that assigns each ordered pair of elements of G an element of G.
A binary operation on a set G, then, is a method by which the members of an ordered pair from G combine to yield a new member of G. This condition is known as closure. The most familiar binary operations are ordinary addition, subtraction, and multiplication of integers. Division of integers is not a binary operation on the integers because an integer divided by an integer need not be an integer.
Q6) Define groups.
A6)
A group is an algebraic structure (G, *) in which the binary operation * on G satisfies the following conditions:
Condition-1: for all a, b, c, ∈ G
a * (b * c) = (a * b) * c (associativity)
Condition-2: there exists an elements e ∈G such that for any a ∈G
a * e= e * a = a (existence of identity)
Condition-3: for every a ∈G, there exists an element denoted by 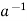 in G such that
in G such that
a *  =
=  * a = e
* a = e
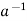 is called the inverse of a in G.
is called the inverse of a in G.
Q7) Give some examples of group.
A7)
Examples of group are-
- (Z, +) is a group where Z denote the set of integers.
- The set {1, 2, . . . , n - 1} is a group under multiplication modulo n if and only if n is prime.
- (R, +) is a group where R denote the set of real numbers.
- The set Z of all integers forms a group with respect to addition; the identity element is 0 and the inverse of a ∈ Z is -a.
- Z is not a multiplicative group since, for example, neither 0 nor 2 has a multiplicative inverse.
- The set A = {1, -1, I, -i} with respect to multiplication on the set of complex numbers forms a group.
Q8) What is the order of a finite group?
A8)
The order of a finite group (G, *) is the number of distinct element in G. The order of
G is denoted by O (G) or by |G|.
Note- A group is called Abelian or non-abelian accordingly as the group operation is or is not commutative.
Q9) If G = {1, -1, i, -i} where i=  , then show that G is an abelian group with respect to multiplication as a binary operation.
, then show that G is an abelian group with respect to multiplication as a binary operation.
A9)
First we will construct a composition table-
. | 1 | -1 | i | -i |
1 | 1 | -1 | i | -i |
-1 | -1 | 1 | -i | i |
i | i | -i | -1 | 1 |
-i | -i | i | 1 | -1 |
It is clear from the above table that algebraic structure (G, .) is closed and satisfies the following conditions.
Associativity- For any three elements a, b, c ∈G (a ⋅b) ⋅c = a ⋅(b ⋅c)
Since
1 ⋅(−1 ⋅i) = 1 ⋅−i= −i
(1 ⋅−1) ⋅i= −1 ⋅i= −i
⇒1 ⋅(−1 ⋅i) = (1 ⋅−1) i
Similarly with any other three elements of G the properties holds.
∴Associative law holds in (G, ⋅)
Existence of identity: 1 is the identity element (G, ⋅) such that 1 ⋅a = a = a ⋅1 ∀a ∈G
Existence of inverse: 1 ⋅1 = 1 = 1 ⋅1 ⇒1 is inverse of 1
(−1) ⋅(−1) = 1 = (−1) ⋅(−1) ⇒–1 is the inverse of (–1)
i⋅(−i) = 1 = −i⋅i⇒–iis the inverse of iin G.
−i⋅i= 1 = i⋅(−i) ⇒iis the inverse of –iin G.
Hence inverse of every element in G exists.
Thus all the axioms of a group are satisfied.
Commutativity: a ⋅b = b ⋅a ∀a, b ∈G hold in G
1 ⋅1 = 1 = 1 ⋅1, −1 ⋅1 = −1 = 1 ⋅−1
i⋅1 = i= 1 ⋅i; i⋅−i= −i⋅i= 1 = 1 etc.
Commutative law is satisfied
Hence (G, ⋅) is an abelian group.
Q10) What are permutation groups?
A10)
Suppose X is a non-empty set. The group of all permutations of X under composition of mapping is called the symmetric group on X and it is denoted by  .
.
A subgroup of 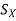 is called a permutation group on X.
is called a permutation group on X.
We can see that a bijection  induces in a natural way an isomorphism
induces in a natural way an isomorphism  .
.
If |X| = n, 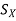 is denoted by
is denoted by 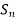 and it is called the symmetric group of degree n.
and it is called the symmetric group of degree n.
A permutation  can be in the form
can be in the form
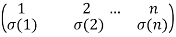
Having two rows of integers, on the top row there are integers- 1, . . . , n and the bottom row has below i for each i = 1,2..n.
below i for each i = 1,2..n.
Which is called the two-row notation for a permutation.
Q11) What do you understand by the group of matrices?
A11)
- The set of all m by n matrices of integer elements, is an infinite Abelian group with matrix addition as composition.
- The set of all n b n non singular matrices having elements as rational numbers is an infinite non-abelian group with matrix multiplication as composition.
The set of n by n non singular matrices having elements as integers is not a group matrix multiplication, for not all such matrices are inversible,
For example:

Determinant of the above matrix is -4 is non-singular but non-invertible in as much there exists no 2 by 2 matrix with elements as integers whose product with the given matrix is the identity matrix.
Q12) Mention the general properties of the group.
A12)
General properties of groups
- Suppose we have a group G, then


Where a ∈ G, b ∈ G and c ∈ G
We have

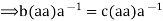
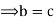
Similarly we can do for left cancellation law.
2. For any given pair of elements a, b of a group G, there exists a unique elements x, y of G such that
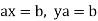
3. General associative law-
For a group, we have
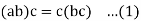
We will now state and prove a generalisation of this associative law for any arbitrary set of n elements.
Suppose an ordered set

Of 4 elements, we can, without changing the order of the elements, consider a number of different associations giving to the corresponding product.
Thus we have
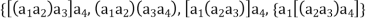
Here is the fact that as a consequences of the associative law (1) holding for three elements. All these products are equal.
The result holds for any arbitrary element.
4. Inverse of the product of an arbitrary number of elements
Suppose a and b are any two elements of a group G, then we have
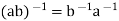
By using the general associative law,
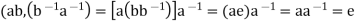
And

By the principal of induction, and the general associative law, we show that

That means that the inverse of the product of any number of elements is equal to the product of the inverses taken in the reverse order.
5. Indices laws
We can easily show that
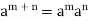

For every a belongs to G and m, n are the integers.
Q13) In a group G, the right and left cancellation laws hold; that is,
Ba = ca implies b = c, and ab = ac implies b = c.
A13)
Suppose ba = ca. Let a’ be an inverse of a. Then, multiplying
On the right by a’ yields (ba)a’ = (ca)a’. Associativity yields b(aa’) = c(aa’). Then, be = ce and, therefore, b = c as desired. Similarly, we can prove that ab = ac implies b = c by multiplying by a’ on the left.
Q14) Define order of a group and element.
A14)
Order of a group- The number of elements of a group (finite or infinite) is called its order. We will use |G| to denote the order of G.
Example: the group Z of integers under addition has infinite order, whereas the group U(10) 5 {1, 3, 7, 9} under multiplication modulo 10 has order 4.
Order of an Element- The order of an element g in a group G is the smallest positive integer n such that 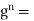 5 e. (In additive notation, this would be ng = 0.) If no such integer exists, we say that g has infinite order. We denote the order of an element g is denoted by |g|.
5 e. (In additive notation, this would be ng = 0.) If no such integer exists, we say that g has infinite order. We denote the order of an element g is denoted by |g|.
Q15) What is a subgroup?
A15)
Let (G, *) be a group and H, be a non-empty subset of G. If (H, *) is itself is a group, then (H, *) is called sub-group of (G, *).
We use the notation H  G to mean that H is a subgroup of G. If we want to indicate that H is a subgroup of G but is not equal to G itself, we write H
G to mean that H is a subgroup of G. If we want to indicate that H is a subgroup of G but is not equal to G itself, we write H 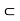 G. Such a subgroup is called a proper subgroup. The subgroup {e} is called the trivial subgroup of G; a subgroup that is not {e} is called a nontrivial subgroup of G.
G. Such a subgroup is called a proper subgroup. The subgroup {e} is called the trivial subgroup of G; a subgroup that is not {e} is called a nontrivial subgroup of G.
Q16) If (G, *) is a group and H ≤G, then (H, *) is a sub-group of (G, *) if and only if
(i) a, b ∈H ⇒a * b ∈H;
(ii) a∈H ⇒ ∈H
∈H
A16)
If (H, *) is a sub-group of (G, *), then both the conditions are obviously satisfied.
We, therefore prove now that if conditions (i) and (ii) are satisfied then (H, *) is a sub-group of (G, *).
To prove that (H, *) is a sub-group of (G, *) all that we are required to prove is : * is associative in
H and identity e ∈H.
That * is associative in H follows from the fact that * is associative in G.
Also,
a∈H ⇒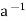 ∈H by (ii) and e ∈H and
∈H by (ii) and e ∈H and 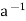 ∈H ⇒a *
∈H ⇒a * 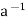 = e ∈H by (i)
= e ∈H by (i)
Hence, H is a sub-group of G.
Q17) Let G be a group and let H be a nonempty subset of G. If ab is in H whenever a and b are in H (H is closed under the operation), and  is in H whenever a is in H (H is closed under taking inverses), then H is a subgroup of G.
is in H whenever a is in H (H is closed under taking inverses), then H is a subgroup of G.
A17)
By above theorem, it suffices to show that a, b 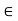 H implies
H implies 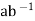
 H. So, we suppose that a, b
H. So, we suppose that a, b 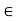 H. Since H is closed under taking inverses, we also have
H. Since H is closed under taking inverses, we also have 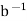
 H. Thus,
H. Thus, 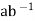
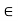 H by closure under multiplication.
H by closure under multiplication.
When applying the “Two-Step Subgroup Test,” we proceed exactly as in the case of the “One-Step Subgroup Test,” except we use the assumption that a and b have property P to prove that ab has property P and that 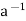 has property P.
has property P.
Example: Let G be the group of nonzero real numbers under multiplication, H = {x 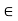 G | x = 1 or x is irrational} and K = {x
G | x = 1 or x is irrational} and K = {x 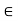 G | x
G | x 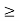 1}. Then H is not a subgroup of G, since
1}. Then H is not a subgroup of G, since 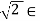 H but
H but 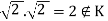 Also, K is not a subgroup, since
Also, K is not a subgroup, since 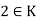 but
but 
 "
"