Unit – 3
Properties of cosets
Q1) What are the cosets?
A1)
Let G be a group and let H be a subset of G. For any a  G, the set {ah | h
G, the set {ah | h  H} is denoted by aH. Analogously, Ha = {ha | h
H} is denoted by aH. Analogously, Ha = {ha | h  H} and aH
H} and aH 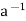 = {ah
= {ah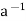 | h
| h 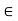 H}. When H is a subgroup of G, the set aH is called the left coset of H in G containing a, whereas Ha is called the right coset of H in G containing a. In this case, the element a is called the coset representative of aH (or Ha). We use |aH| to denote the number of elements in the set aH, and |Ha| to denote the number of elements in Ha.
H}. When H is a subgroup of G, the set aH is called the left coset of H in G containing a, whereas Ha is called the right coset of H in G containing a. In this case, the element a is called the coset representative of aH (or Ha). We use |aH| to denote the number of elements in the set aH, and |Ha| to denote the number of elements in Ha.
Q2) Give the properties of cosets.
A2)
Let H be a subgroup of G, and let a and b belong to G. Then,
1. a aH,
aH,
2. AH = H if and only if a 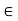 H,
H,
3. AH = bH if and only if a  bH
bH
4. AH = bH or aH 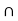 bH =
bH = 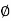 ,
,
5. AH = bH if and only if  b [ H,
b [ H,
6. |aH| = |bH|,
7. AH = Ha if and only if H = aH 1,
1,
8. AH is a subgroup of G if and only if a 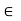 H.
H.
Q3) Let G be a group. A be non empty subset H of G is a subgroup of G iff either of the following rules holds
- For all a, b
 , ab
, ab  and inverse of a
and inverse of a 
- For all a, b
 ,
, 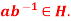
A3)
If H is a subgroup the both the conditions above are true. Conversely suppose H satisfies the condition first then for any 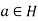 ,
,  .
.
Hence, e = 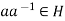 . Therefore, H is a subgroup.
. Therefore, H is a subgroup.
Now suppose that H follows the second rule.
Let 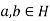 . Then
. Then 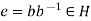 .
.
Hence 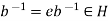 .
.
Therefore 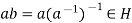 , which proves that H is a subgroup of G.
, which proves that H is a subgroup of G.
Q4) let  be a homomorphism of groups, then prove that ker
be a homomorphism of groups, then prove that ker  is a subgroup of G and Im
is a subgroup of G and Im  is a subgroup of H.
is a subgroup of H.
A4)
Ker  and Im
and Im  both are non empty. Let
both are non empty. Let 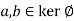 then
then 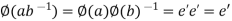 where e’ is the identity of G.
where e’ is the identity of G.
Hence  . This proves that ker
. This proves that ker  is a subgroup of G.
is a subgroup of G.
Now let  then
then  for some x, y
for some x, y .
.
Hence 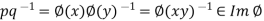 , which proves that Im
, which proves that Im 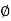 is the subgroup of H.
is the subgroup of H.
Q5) Let H and K be subgroups of a group (G, .), then HK is a subgroup of G iff HK = KH.
A5)
Let HK = KH. Since e = ee 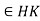 , HK is not empty.
, HK is not empty.
Let 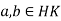 then
then 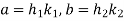 for some
for some  . Hence
. Hence
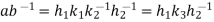
Where 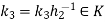 .
.
Now  hence
hence 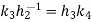 for some
for some  , therefore
, therefore

Where 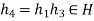 hence
hence 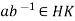 .
.
This proves that HK is a subgroup.
Conversely, suppose that HK is a subgroup, let  , so that a = kh for some
, so that a = kh for some  . Then
. Then 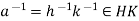 . Hence
. Hence 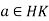 .
.
Therefore, KH is subgroup of HK.
Now let  . Then
. Then  . Hence
. Hence  for some
for some  . Therefore
. Therefore 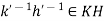 . Hence HK
. Hence HK 
Q6) Let G be a group and 
- If
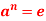 for some integer
for some integer  then o(a)|n
then o(a)|n - If o(a) = m, then for all integers I,
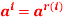 , where r(i) is the remainder of I modulo m.
, where r(i) is the remainder of I modulo m. - [a] is of order m iff o(a) = m
A6)
Part-1: if 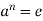 then
then 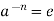 , hence
, hence  for some i > 0. Therefore by the well ordering property of N, there is a least +ve integer m = 0(a) such that
for some i > 0. Therefore by the well ordering property of N, there is a least +ve integer m = 0(a) such that 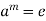 .
.
By using division algorithm, n = mq + r, 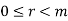 .
.
Hence  . Therefore r = 0 and m|n.
. Therefore r = 0 and m|n.
Part-2: Again using division algorithm, for any 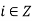 , i = mq + r,
, i = mq + r,  . Hence
. Hence 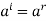 , where r = r(i) is the remainder of i modulo m.
, where r = r(i) is the remainder of i modulo m.
Part-3: Let o(a) = m then 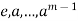 are distinct, for otherwise
are distinct, for otherwise  for some I, j,
for some I, j,  . Hence,
. Hence, 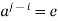 , a contradiction.
, a contradiction.
Let H = [a] be the cyclic subgroup generated by a.
For any 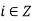 ,
, 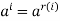 . This implies that H has exactly m elements
. This implies that H has exactly m elements 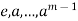 .
.
Conversely, suppose H is of finite order. Then 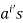 are not distinct for all
are not distinct for all 
Hence  for some
for some  . Then
. Then  . Hence a is of finite order, say m but then H has exactly m elements as proved earlier.
. Hence a is of finite order, say m but then H has exactly m elements as proved earlier.
Q7) Define left and right coset.
A7)
Let H be a subgroup of G. Given 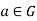 , the set
, the set
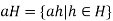
Is called the left coset of H determined by a.
A subset C of G is called a left coset of H in G if C = aH for some a in G.
The set of all cosets of H in G can be written as G/H.
A right coset Ha us defined similarly.
The set of all right cosets of H in G is written as H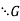 .
.
Definition: Let H be a subgroup of G. The cardinal number of the set of left and right cosets of H in G is called the index of H in G and it is denoted by [G:H].
Note- Let G be a finite group and let H be any subgroup of G. Let |G| = n and |H| = m then every left coset of H has m elements.
Since the distinct left coset of H are pairwise disjoint and their union is G, we must have n = km, where k is the number of left cosets of H in G.
Q8) State and prove Lagrange’s theorem.
A8)
Statement- If G is a finite group and H is a subgroup of G, then |H| divides |G|. Moreover, the number of distinct left (right) cosets of H in G is |G|/|H|.
Proof:
Let  H,
H, 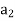 H, . . . ,
H, . . . , 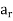 H denote the distinct left cosets of H in G. Then, for each a in G, we have aH =
H denote the distinct left cosets of H in G. Then, for each a in G, we have aH = 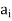 H for some i. Also, by property 1 of the lemma, a
H for some i. Also, by property 1 of the lemma, a 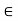 aH. Thus, each member of G belongs to one of the cosets aiH. In symbols,
aH. Thus, each member of G belongs to one of the cosets aiH. In symbols,
G =  H
H  . . . .
. . . . 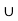
 H.
H.
Now, property 4 of the lemma shows that this union is disjoint, so that
|G| = |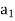 H| + |
H| + | H| + ……+ |
H| + ……+ |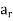 H|.
H|.
Finally, since | H| = |H| for each i, we have |G| = r|H|.
H| = |H| for each i, we have |G| = r|H|.
Note- The converse of Lagrange’s Theorem is false. For example, a group of order 12 need not have a subgroup of order 6.
Q9) For every integer a and every prime p, 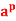 mod p = a mod p.
mod p = a mod p.
A9)
By the division algorithm, a = pm + r, where 0  r , p. Thus, a mod p = r, and it suffices to prove that
r , p. Thus, a mod p = r, and it suffices to prove that 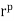 mod p = r. If r = 0, the result is trivial, so we may assume that r
mod p = r. If r = 0, the result is trivial, so we may assume that r  U(p). [Recall that U(p) = {1, 2, . . . , p 2 1} under multiplication modulo p.] Then, by the above corollary,
U(p). [Recall that U(p) = {1, 2, . . . , p 2 1} under multiplication modulo p.] Then, by the above corollary, 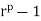 mod p = 1 and, therefore,
mod p = 1 and, therefore, 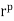 mod p 5 r.
mod p 5 r.
Q10) Explain orbit of a point with the help of example.
A10)
Let G be a group of permutations of a set S. For each s in S, let orbG(s) = { (s) |
(s) | 
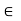 G}. The set orbitG(s) is a subset of S called the orbit of s under G. We use |orbG(s)| to denote the number of elements in orbG(s).
G}. The set orbitG(s) is a subset of S called the orbit of s under G. We use |orbG(s)| to denote the number of elements in orbG(s).
Example: Let G 5 {(1), (132)(465)(78), (132)(465), (123)(456), (123)(456)(78), (78)}.
Then
OrbG(1) 5 {1, 3, 2}, stabG(1) 5 {(1), (78)},
OrbG(2) 5 {2, 1, 3}, stabG(2) 5 {(1), (78)},
OrbG(4) 5 {4, 6, 5}, stabG(4) 5 {(1), (78)},
OrbG(7) 5 {7, 8}, stabG(7) 5 {(1), (132)(465), (123)(456)}.
Q11) What do you understand by the external direct product?
A11)
Let G1, G2, . . . , Gn be a finite collection of groups. The external direct product of G1, G2, . . . , Gn, written as G1  G2
G2  …
…  Gn, is the set of all n-tuples for which the ith component is an element of Gi and the operation is componentwise.
Gn, is the set of all n-tuples for which the ith component is an element of Gi and the operation is componentwise.
In symbols,

Where (g1, g2, . . . , gn)(g1’, g2’, . . . , gn’) is defined to be (g1g1’, g2g2’, . . . , gngn’). It is understood that each product gigi ‘ is performed with the operation of Gi.
Example:
U(8)  U(10) = {(1, 1), (1, 3), (1, 7), (1, 9), (3, 1), (3, 3), (3, 7), (3, 9), (5, 1), (5, 3), (5, 7), (5, 9), (7, 1),(7, 3), (7, 7), (7, 9)}.
U(10) = {(1, 1), (1, 3), (1, 7), (1, 9), (3, 1), (3, 3), (3, 7), (3, 9), (5, 1), (5, 3), (5, 7), (5, 9), (7, 1),(7, 3), (7, 7), (7, 9)}.
Q12) What is an order of an element in a Direct Product.
A12)
The order of an element in a direct product of a finite number o finite groups is the least common multiple of the orders of the components of the element.
Symbolically

Proof:
Denote the identity of Gi by ei. Let S =
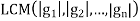
And
t = 
Because s is a multiple of each |gi| implies that
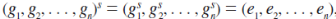
We know that t s. On the other hand, from
s. On the other hand, from

We see that t is a common multiple of  . Thus
. Thus 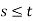 .
.
Q13) Define normal subgroup.
A13)
A subgroup H of a group G is called a normal subgroup of G if aH = Ha for all a in G. We denote this by H 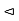 G.
G.
In other words we can define it as-
Let G be a group. A subgroup N of G is called a normal subgroup of G, written as N  G, if
G, if  for every
for every  .
.
Note- If G is abelian then every subgroup of G is a normal subgroup, but the converse is not same.
A group in which every subgroup is normal is not necessarily abelian.
Q14) let N be a normal subgroup of the group G. Then G/N is a group under multiplication. The mapping  , given by
, given by  , is a surjective homomorphism and
, is a surjective homomorphism and 
A14)
By the properties above (xN)(Yn) = (xy)N for all  . Hence, G/N is closed under multiplication, because multiplication is associative in G, multiplication is also associative in G/N.
. Hence, G/N is closed under multiplication, because multiplication is associative in G, multiplication is also associative in G/N.
The coset eN = N is the identity for multiplication in G/N, and for any  ,
,
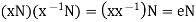
This proves that G/N is a group.
The mapping  is a homomorphism. Further, xN = eN iff
is a homomorphism. Further, xN = eN iff 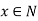 .
.
Hence ker  .
.
Q15) Let G be a group. For any non-empty subset S of G, N(S) is a subgroup of G, further, for any subgroup H of G,
- N(H) is the largest subgroup of G in which H is normal
- If K is a subgroup of N(H), then H is a normal subgroup of KH.
A15)
Clearly if 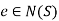 , if x, y
, if x, y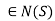 , then
, then

Hence 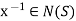 , therefore, N(S) is a subgroup of G.
, therefore, N(S) is a subgroup of G.
Let H is a subgroup of G, then  for all
for all 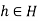 , therefore H is a subset, hence a subgroup of N(H).
, therefore H is a subset, hence a subgroup of N(H).
Further by the definition 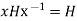 for all
for all .
.
Hence H 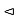 N(H).
N(H).
Let K be any subgroup of G such that H  .
.
Then 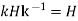 for all
for all 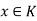 .
.
Hence K is subset of N(H). This proves that N(H) is the largest subgroup of G containing H as normal subgroup.
Let K be a subgroup of N(H), then for all  hence kH = Hk, therefore KH = HK.
hence kH = Hk, therefore KH = HK.
Hence by the theorem KH is a subgroup of N(H), and H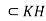 , consequently H
, consequently H 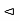 HK.
HK.
Q16) Let G be a group, and let G’ be the derived group of G.
Then
- G’
 G.
G. - G/G’ is abelian
- If H
 G, then G/H is abelian iff G’
G, then G/H is abelian iff G’ .
.
A16)
- Suppose
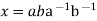 be any commutator in G. Then
be any commutator in G. Then  is also a commutator, moreover for any g in G,
is also a commutator, moreover for any g in G,
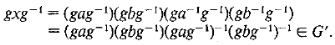
Now any element y in G’ is a product of a finite number of commutators,
Say

Where 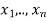 are commutators. Then for any
are commutators. Then for any 
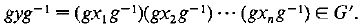
Hence, G’ is a normal subgroup of G.
2. For all 
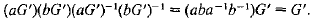
Hence (aG’)(bG’) = (bG’)(aG’). Therefore G/G’ is abelian.
3. Suppose G/H is abelian. Then for all 
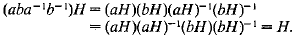
Hence, 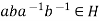 . This proves that
. This proves that 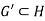 .
.
We can prove the converse similarly.
Q17) Let G be a group and let H be a normal subgroup of G. The set G/H = {aH | a  G} is a group under the operation (aH)(bH) = abH
G} is a group under the operation (aH)(bH) = abH
A17)
First we need to show that the operation is well defined; that is, we must show that the correspondence defined above from G/H  G/H into G/H is actually a function. To do this we assume that for some elements a, a’, b, and b’ from G, we have aH = a’H and bH = b’H and verify that aHbH = a9Hb’H. That is, verify that abh = a’b’H. (This shows that the definition of multiplication depends only on the cosets and not on the coset representatives.) From aH = a’H and bH = b’H , we have a’ = ah1 and b’ = bh2 for some h1, h2 in H, and therefore
G/H into G/H is actually a function. To do this we assume that for some elements a, a’, b, and b’ from G, we have aH = a’H and bH = b’H and verify that aHbH = a9Hb’H. That is, verify that abh = a’b’H. (This shows that the definition of multiplication depends only on the cosets and not on the coset representatives.) From aH = a’H and bH = b’H , we have a’ = ah1 and b’ = bh2 for some h1, h2 in H, and therefore
a’b’H = ah1bh2H = ah1bH = ah1Hb = aHb = abH. Here we have made multiple use of associativity, and the fact that H  G. eH = H is the identity;
G. eH = H is the identity; 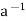 H is the inverse of aH; and (aHbH)cH = (ab)HcH = (ab)cH = a(bc)H = aH(bc)H = aH(bHcH). This proves that G/H is a group.
H is the inverse of aH; and (aHbH)cH = (ab)HcH = (ab)cH = a(bc)H = aH(bc)H = aH(bHcH). This proves that G/H is a group.
Q18) State and prove the Cauchy’s Theorem for Abelian Groups
A18)
Statement- Let G be a finite Abelian group and let p be a prime that divides the order of G. Then G has an element of order p.
Proof:
The statement is true for the case in which G has order 2. We prove the theorem by using the Second Principle of Mathematical Induction on |G|. That is, we assume that the statement is true for all Abelian groups with fewer elements than G and use this assumption to show that the statement is true for G as well. Certainly, G has elements of prime order, for if |x| = m and m = qn, where q is prime, then |; 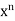 | = q. So let x be an element of G of some prime order q, say. If q = p, we are finished; so assume that q in not equals p. Since every subgroup of an Abelian group is normal, we may construct the factor group
| = q. So let x be an element of G of some prime order q, say. If q = p, we are finished; so assume that q in not equals p. Since every subgroup of an Abelian group is normal, we may construct the factor group  = G/<x>. Then
= G/<x>. Then  is Abelian and p divides |
is Abelian and p divides | |, since |
|, since | | = |G|/q. By induction, then,
| = |G|/q. By induction, then, 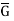 has an element—call it y<x> —of order p.
has an element—call it y<x> —of order p.