Unit - 4
Cauchy's theorem for finite abelian groups
Q1) State and prove Cauchy's theorem for finite abelian groups.
A1)
Let G be a finite Abelian group and let p be a prime that divides the order of G. Then G has an element of order p.
Proof:
The statement given above is true for the case in which G has order 2. We prove the theorem by using the Second Principle of Mathematical Induction on |G|. That is, we assume that the statement is true for all Abelian groups with fewer elements than G and use this assumption to show that the statement is true for G as well. Certainly, G has elements of prime order, for if |x| = m and m = qn, where q is prime, then |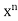 | = q. So let x be an element of G of some prime order q, say.
| = q. So let x be an element of G of some prime order q, say.
If q = p, we are finished; so assume that q 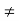 p. Since every subgroup of an Abelian group is normal, we may construct the factor group
p. Since every subgroup of an Abelian group is normal, we may construct the factor group  G/{x}. Then
G/{x}. Then is Abelian and p divides |
is Abelian and p divides |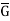 |, since |
|, since | | = |G|/q. By induction, then,
| = |G|/q. By induction, then, 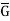 has an element- call it y{x} - of order p.
has an element- call it y{x} - of order p.
Q2) Define homomorphism.
A2)
Suppose we have two groups G and G’. We shall suppose that the composition in both the groups are denoted multiplicatively.
Then we say that G is homomorphic to G’ or that G’ is a homomorphic image of G if there exists a mapping f of G onto G’ such that
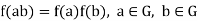
Also, then f is said to be a homomorphic mapping or a homomorphism of G onto G’.
We express this relation of homomorphism by-

Note- if G is homomorphic to G’, then there may exist more than one homomorphism of G onto G’.
Q3) Explain normal subgroup.
A3)
A Subgroup N of a group G is called a Normal Subgroup of G if it is invariant under conjugation that is the conjugation of an element of N by an element of G is always in N. The usual notation for this relation is N G, and the definition may be written in symbol as
G, and the definition may be written in symbol as
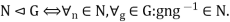
Congruence Relations: If a and b are integers and m is a positive integer, them a is congruent to b modulo m if m divides a-b.
- The notation a
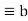 (mod m) says that a is congruent to b modulo m.
(mod m) says that a is congruent to b modulo m. - We say that a
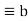 (mod m) is a congruence and that m is its modulus.
(mod m) is a congruence and that m is its modulus. - Two integers are congruent mod m if and only if they have the same remainder when divided by m.
- If a is not congruent to b modulo m, we write a
 b (mod m)
b (mod m)
Q4) Let  be a group homomorphism, and let H=ker(
be a group homomorphism, and let H=ker( ). Let a
). Let a Then, the set
Then, the set  is the left coset aH of H, and is also the right coset Ha of H, Consequently, the two partitions of G into left cosets and into right cosets of H are the same.
is the left coset aH of H, and is also the right coset Ha of H, Consequently, the two partitions of G into left cosets and into right cosets of H are the same.
A4)
Proof: (a) It is a homomorphism, because
(b) It is not a homomorphism, because 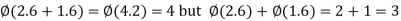 .
.
(c) It is a homomorphism, because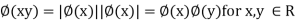 *
*
(d) It is a homomorphism, because 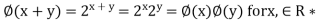
Q5) The following are three equivalent conditions for a subgroup H to be a normal subgroup of a group G.
1.
2.
3.
A5)
Proof: (1)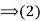 Suppose that H is a subgroup of G such that
Suppose that H is a subgroup of G such that  for all g
for all g and all h
and all h Then
Then 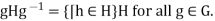
We claim that actually 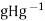 =H.We must show that H
=H.We must show that H for all g
for all g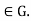
Let h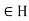 . Replacing g by
. Replacing g by  in the relation
in the relation  , we obtain
, we obtain 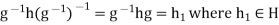 .
.
Consequently,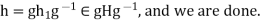
(3)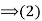 Suppose that gH=Hg for all g
Suppose that gH=Hg for all g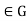 . Then
. Then 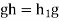 , So
, So  for all g
for all g
And all  By the preceding paragraph, this means that
By the preceding paragraph, this means that 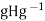 =H for all g
=H for all g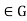 .
.
(2)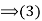 Conversely, if
Conversely, if 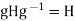 for all g
for all g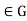 then
then  =
= gH
gH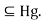 But also,
But also, 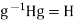 giving
giving  ,so that hg=g
,so that hg=g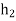 and Hg
and Hg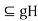 .
.
Q6) Prove that congruence modulo n is an equivalence relation on Z.
A6)
1) Reflexivity: For any a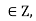 we have
we have  because a-a = 0 is divisible by n. Hence relation is reflexive.
because a-a = 0 is divisible by n. Hence relation is reflexive.
2) Symmetry: suppose a  b (mod n)
b (mod n)
 is divisible by n
is divisible by n 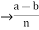 = k, for some k
= k, for some k 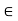 z
z  a-b = nk
a-b = nk
Therefore, b-a = -(a-b) = -nk= n(-k)
Thus, the relation is symmetric.
3) Transitivity: Suppose a  b (mod n) and b
b (mod n) and b  c (mod n), then
c (mod n), then  = k and
= k and 
By adding these two equations we get, a-c = n(k+1) 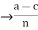 = k+l
= k+l
So, a-c is divisible by n as k+1  Z, i.e., a
Z, i.e., a  c (mod n)
c (mod n)
Thus, the relation is transitive.
Hence this is an equivalence relation on Z.
Q7) Define the Kernel of a homomorphism.
A7)
If f is a homomorphism of G onto G’, then the set H of all those elements of G which are mapped on the identity e’ of G’, which means the sub-set  is a normal subgroup of the same.
is a normal subgroup of the same.
Let 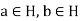 so that
so that
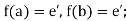
e’ being the identity of G’.
We then have
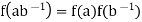
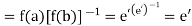
Thus
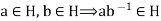
And hence H is a subgroup of G
Again, if x is any member of G, we have

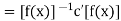
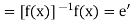
So that

Hence H is normal subgroup of G.
Q8) Let G be (Z, +) i.e., the group of integers under addition and let f: G → G defined by
∅(x) = 3x ∀x ∈G. Prove that f is homomorphism, determine its Kernel.
A8)
We have ∅(x) = 3x ∀x ∈G
∀x, y ∈G ⇒x + y ∈G (∴G is a group under addition)
Now
f (x + y) = 3 (x + y)
= 3x + 3y
= f (x) + f (y)
Hence f is homomorphism.
Kernel of homomorphism consists of half of zero i.e., the integers whose double is zero.
Thus K = {0}
Q9) The following are three equivalent conditions for a subgroup H to be a normal subgroup of a group G.
1.
2.
3.
A9)
(1) Suppose that H is a subgroup of G such that
Suppose that H is a subgroup of G such that  for all g
for all g and all h
and all h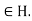 Then
Then 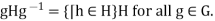
We claim that actually 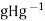 =H.We must show that H
=H.We must show that H for all g
for all g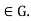
Let h . Replacing g by
. Replacing g by  in the relation
in the relation 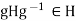 , we obtain
, we obtain  .
.
Consequently,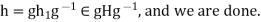
(3) Suppose that gH=Hg for all g
Suppose that gH=Hg for all g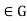 . Then
. Then  , So
, So  for all g
for all g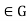
And all  By the preceding paragraph, this means that
By the preceding paragraph, this means that  =H for all g
=H for all g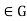 .
.
(2)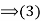 Conversely, if
Conversely, if  for all g
for all g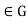 then
then 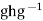 =
= gH
gH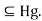 But also,
But also,  giving
giving  ,so that hg=g
,so that hg=g and Hg
and Hg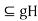 .
.
Example: Prove that congruence modulo n is an equivalence relation on Z.
Solution:
1) Reflexivity: For any a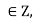 we have
we have 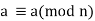 because a-a = 0 is divisible by n. Hence relation is reflexive.
because a-a = 0 is divisible by n. Hence relation is reflexive.
2) Symmetry: suppose a  b (mod n)
b (mod n)
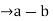 is divisible by n
is divisible by n 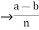 = k, for some k
= k, for some k 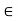 z
z  a-b = nk
a-b = nk
Therefore, b-a = -(a-b) = -nk= n(-k)
Thus, the relation is symmetric.
3) Transitivity: Suppose a  b (mod n) and b
b (mod n) and b  c (mod n), then
c (mod n), then 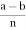 = k and
= k and 
By adding these two equations we get, a-c = n(k+1)  = k+l
= k+l
So, a-c is divisible by n as k+1  Z, i.e., a
Z, i.e., a  c (mod n)
c (mod n)
Thus, the relation is transitive.
Hence this is an equivalence relation on Z.
Q10) Explain Cayley’s theorem.
A10)
Cayley’s theorem- Every finite group G is isomorphic to a permutation group.
Proof:
Let G be a finite group of order n and that its n elements, in some order are
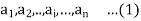
Let b is any element of G so that it is one of the elements in the set (1),
Then
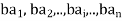
Are all different elements of G and they are the elements of G written in different order,
In fact

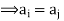
Thus
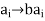
Is a one-one mapping of the set (1) onto itself so that

Which is a permutation of n degree.
Here we will use the notation for this as below
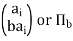
Hence, we see that we have a permutation of degree n,
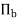 corresponding to each
corresponding to each 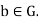
Suppose G’ denotes the set of all permutations 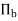 corresponding to the elements of the set (1).
corresponding to the elements of the set (1).
Now consider the mapping
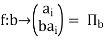
This mapping of G onto G’ is one-one for
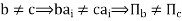
Again

Thus, we see that we have a one-one mapping f of the group G onto a set G’ of permutations such that

Thus G’ is a group isomorphic to the group G.
Q11) Define isomorphism.
A11)
Let (s, *) and (S’, *) be two semi group. A function f: S S’ is called an isomorphism if s is one to one and onto and if
f(a+b) =f(a)*f(b). For all a, b in S
Procedure to find the isomorphism
Step 1: we do in the function f: S S’ with domain of f=S
Step 2: We shall show that f is one to one.
Step 3: We shall show that f is onto.
Step 4: We shall show that f(a*b) = f(a)*’ f(b).
Q12) List the properties of Isomorphisms Acting on Groups
A12)
Suppose that  is an isomorphism from a group
is an isomorphism from a group  onto a group
onto a group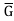 then
then
1.  is an isomorphism from
is an isomorphism from 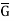 onto G.
onto G.
2. G is Abelian if and only if  is Abelian.
is Abelian.
3. G is cyclic if and only if 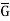 is cyclic.
is cyclic.
4. If K is a subgroup of G, then  (K) = {
(K) = { (k) | k
(k) | k 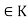 } is a subgroup of G.
} is a subgroup of G.
Q13) What is the first isomorphism theorem?
A13)
This theorem is also known as fundamental theorem of homomorphism.
According to this theorem every homomorphic image of G is isomorphic to a quotient group of G.
In other words,
Let 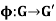 be a homomorphism of groups, then
be a homomorphism of groups, then
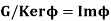
Hence, in particular, 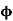 is surjective then
is surjective then
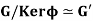
Proof:
Consider the mapping,

Given by 
Where K = Ker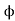 , for any
, for any 
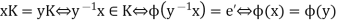
Hence, 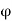 is well defined and injective, further
is well defined and injective, further

Hence 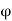 is a homomorphism. Since
is a homomorphism. Since 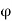 is obviously surjective, we conclude that
is obviously surjective, we conclude that  is an isomorphism of groups.
is an isomorphism of groups.
Q14) What is the third isomorphism theorem?
A14)
Suppose H and K be normal subgroups of G and  then
then

Note- this theorem is also known as “double quotient isomorphism theorem.”
Proof:
Let the mapping
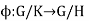
Given by 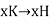
The mapping is well defined, for
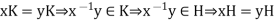
Further, for all 
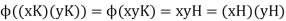
Hence  is a homomorphism. Now
is a homomorphism. Now  is obviously surjective, and
is obviously surjective, and

Hence, by the first isomorphism theorem,