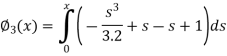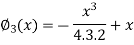Unit - 4
Systems of linear differential equations
Q1) What is the general linear system of two first order differential equations in two unknown functions?
A1)
The general linear system of two first order differential equations in two unknown functions x and y is of the form
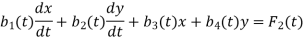
For example: 
Q2) Define the Matrix form of system of linear differential equations.
A2)
Suppose the system of linear differential equations is gives as below
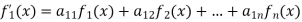
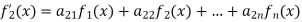
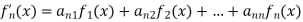
This system is written as
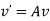
Where
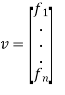
And
Q3) What do you understand by the basic type of system of two linear differential equations?
A3)
Let us consider a basic type of system of two linear differential equations in two unknown functions. This is of the form
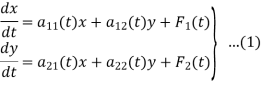
We will assume that the functions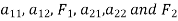 
are all continuous on a real interval 
If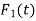 
and 
are zero for all t, then the above system is called homogeneous, otherwise the system is called non-homogeneous.
For example:
Is homogenous,
And the system
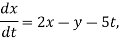
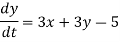
Is non-homogeneous.
Q4) Solve 
A4)
Its auxiliary equation is-
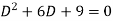
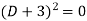
Where-
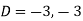
Therefore the complete solution is-
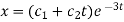
Q5) Find the P.I. Of (D + 2)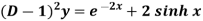
A5)
P.I. =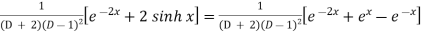 
Now we will evaluate each term separately-
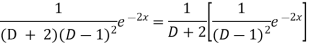
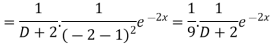
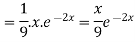
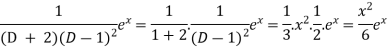
And
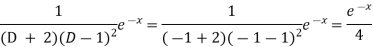
Therefore-
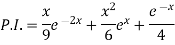
Q6) Solve (D – D’ – 2 ) (D – D’ – 3) z =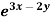 
A6)
The C.F. Will be given by-
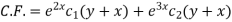
Particular integral-
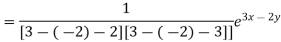
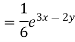
Therefore the complete solution is-
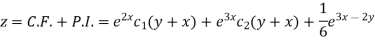
Q7) Find the P.I. Of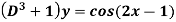 
A7)
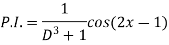
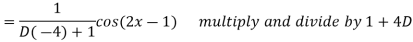
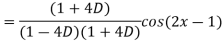
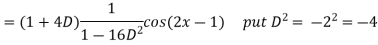
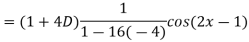
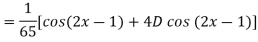
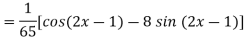
Q8) Find P.I. Of
A8)
P.I = 
Replace D by D+1
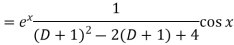
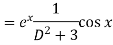
Put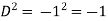 
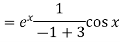
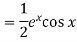
Q9) Solve 
A9)
Auxiliary equation 
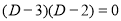
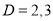
C.F is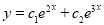 
[
]
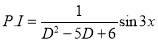
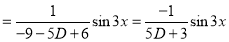
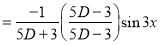
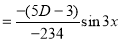
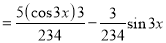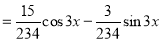
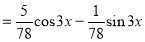
The Complete Solution is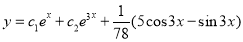 
Q10) Solve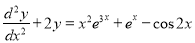 
A10)
The Auxiliary equation is 
The C.F is
P.I 
Now,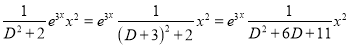 
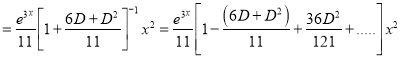
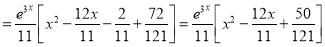
The Complete Solution is
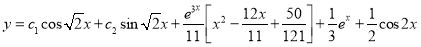
Q11) Solve 
A11)
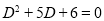
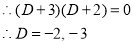
The auxiliary equation is 
The C.F is 
[Put 
]
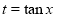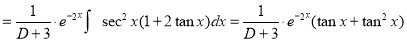
The Complete Solution is 
Q12) Solve 
A12)
The auxiliary equation is 
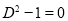
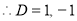
The C.F is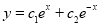
Here 
, 
, 
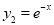. Let 
Now, 
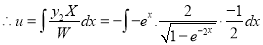
Put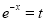 
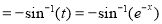
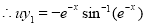
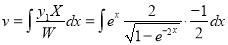
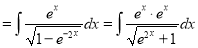
Multiply by 
in the numerator and denominator
Put 
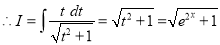
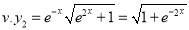
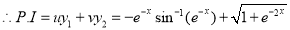
The Complete Solution is 
Q13) What is the method of successive approximations?
A13)
Suppose dy/dx = f(x, y) is a first order ODE and with the initial condition y(0) = 0 and if f and 
are continuous on rectangle R for which the 
then 
where y = 
is the unique solution to this initial value problem.
Now the functions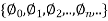 
are successive approximations of the unique solution y = 
.
Hence we begin with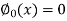 
, and the other functions can be find by using the formula given below
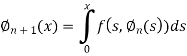
Q14) By using the method of successive approximation find the functions 
of the following differential equation
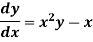
With the initial condition y(0) = 0.
A14)
Suppose 
, here f is continuous on all of 
and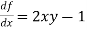 
is continuous on all of 
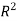, hence the unique solution exists.
Now define 
Here we will calculate the three approximations,
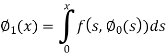
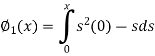
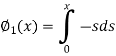
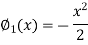
Similarly
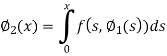
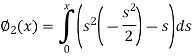
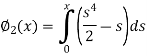
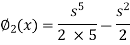
Now the third approximations will be
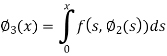
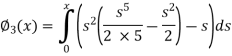
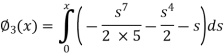
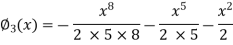
Q15) By using the method of successive approximation find the functions 
of the following differential equation
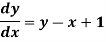
With the initial condition y(0) = 0.
A15)
Suppose 
, here f is continuous on all of 
and 
is continuous on all of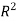 
, hence the unique solution exists.
Now define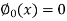 
Here we will calculate the three approximations,
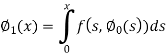
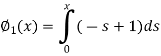
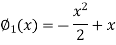
Now
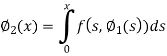
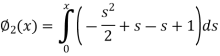
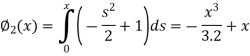
And
