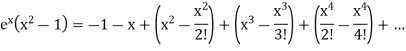Unit – 1
L’ Hospital’s Rules
Q1) What do you understand by indeterminate forms?
A1)
Let we have two functions f(x) and g(x) and-

Then-
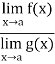
Is an expression of the form  .
.
In that case we can say that f(x)/g(x) is an indeterminate for of the type  at x = a.
at x = a.
Now, Let we have two functions f(x) and g(x) and-
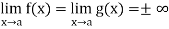
Then-
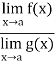
Is an expression of the form  , in that case we can say that f(x)/g(x) is an indeterminate for of the type
, in that case we can say that f(x)/g(x) is an indeterminate for of the type  at x = a.
at x = a.
Some other indeterminate forms are 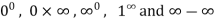
Q2) What is L’Hospital rules for 0/0 indeterminate form?
A2)
L’Hospital’s rule for  form-
form-
Working steps-
1. Check that the limits f(x)/g(x) is an indeterminate form of type  .
.
(Note- we can not apply L’Hospital rule if it is not in indeterminate form)
2. Differentiate f and g separately.
3. Find the limits of the derivatives. If the limit is finite ,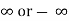 then it is equal to the limit of f(x)/g(x).
then it is equal to the limit of f(x)/g(x).
Q3) Evaluate 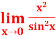 .
.
A3)
Let f(x) =  and g(x) =
and g(x) =  .
.
Here we see that this is the indeterminate form of 0/0 at x = 0.
Now by using L’Hospital rule, we get-

= 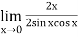
= 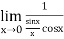
=  = 1
= 1
Q4) Evaluate 
A4)
Let f(x) =  , then
, then
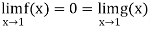
And
 = 0
= 0
 = 0
= 0
But if we use L’Hospital rule again, then we get-
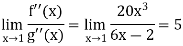
Q5) Evaluate 
A5)
Here we find that-
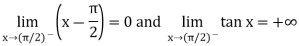
So that this limit is the form of 0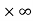 .
.
Now,
Change 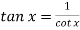 to obtain the limit-
to obtain the limit-

Now this is the form of 0/0,
Apply L’Hospital’s rule-
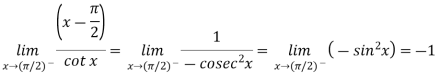
Q6) State and prove Cauchy’s mean value theorem.
A6)
Suppose we have two functions f(x) and g(x) of x, such that,
1. Both functions are continuous in [a, b]
2. Both functions are differentiable in (a, b)
3. g’(x) ≠ 0 for any x ϵ (a, b)
These three exists atleast, x = c ϵ (a, b), at which
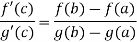
Proof:
Suppose, we define a functions,
h(x) = f(x) – A.g(x) …………………….(1)
So that h(a) = h(b) and A is a constant to be determined.
Now,
h(a) = f(a) – Ag(a)
h(b) = f(b) – Ag(b)
So that,
f(a) – Ag(a) = f(b) – A.g(b),
Which gives
A = 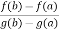 …………………………….(2)
…………………………….(2)
Now, h(x) is continuous in [a, b] as RHS of eq. (1) is continuous in [a,b] and h(x) is diff. In (a, b) as RHS of eq. (1) is diff. In (a, b)
Also,
h(a) = h(b)
Therefore all the conditions of Rolle’s theorem are satistfied then there exists a Value x = cϵ (a, b)
So that h’(c) = 0
Differentiate eq.(1) w.r.t. x , we get
h’(x) = f’(x) – A.g’(x)
At x = c
h’(c) = f’(c) – A.g’(c)
0 = f’(c) – A.g’(c)
A = 
So that , we get
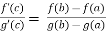 where a<c<b
where a<c<b
Hence the Cauchy’s mean value theorem is proved.
Q7) Verify Cauchy’s mean value theorem for the function f(x) = x⁴ and g(x) = x² in the interval [1,2]
A7)
We are given, f(x) = x⁴ and g(x) = x
Derivative of these functions,
f’(x) = 4x³ and g’(x) = 2x
Put these values in Cauchy’s formula, we get
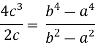
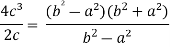
2c² = 
c² = 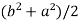
c = 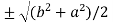
Now put the values of a = 1 and b = 2 ,we get
c =  =
= =
=  (approx)
(approx)
Hence the Cauchy’s theorem is verified.
Q8) Examine the function  for extreme values.
for extreme values.
A8)
Suppose
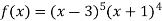
Then

Hence the function is derivable for all x  and the derivative f’ vanishes for x = -1, 3 and 7/9 which we may test for extreme values.
and the derivative f’ vanishes for x = -1, 3 and 7/9 which we may test for extreme values.
- For x = -1
f’ is positive for a value of x less than -1 and negative for greater than -1.
Thus f’ changes sign from + to – as x passes through -1.
Hence -1 is a point of maximum
2. X = 3
F’ remains positive as x passes through 3.
So that x= 3 is
Q9) Prove that 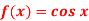 Then
Then
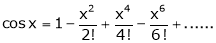
A9)
Let f(x) = cos x
Then by Maclaurin’s series,
 … (1)
… (1)
Since


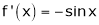

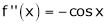
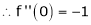

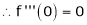

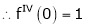
 From Equation (1)
From Equation (1)
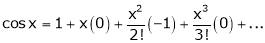

Q10) If 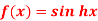 Then
Then
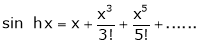
A10)
Here f(x) = sin hx.
 By Maclaurin’s expansion,
By Maclaurin’s expansion,
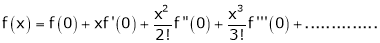 (1)
(1)

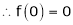
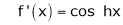


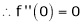
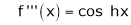
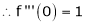
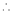 By equation (1) we get,
By equation (1) we get,
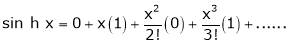
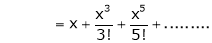
Q11) If  then
then
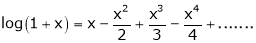
A11)
Here f(x) = log (1 + x)
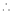 By Maclaurin’s series expansion,
By Maclaurin’s series expansion,
 … (1)
… (1)



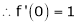
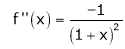


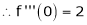


 By equation (1)
By equation (1)
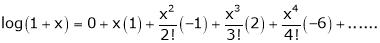

Q12) Expand by, Maclaurin’s theorem 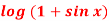
A12)
Here f(x) = log (1 + sin x)
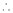 By Maclaurin’s Theorem,
By Maclaurin’s Theorem,
 … (1)
… (1)

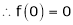
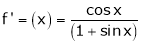


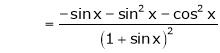

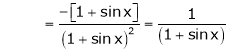
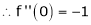
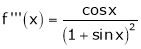
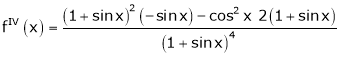
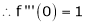
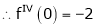 ……..
……..
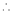 equation (1) becomes,
equation (1) becomes,

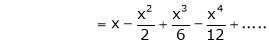
Q13) Expand by Maclaurin’s theorem, log sec x
A13)
Let f(x) = log sec x
 By Maclaurin’s Expansion’s,
By Maclaurin’s Expansion’s,
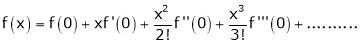 (1)
(1)

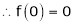
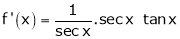


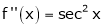
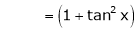
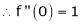
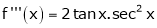
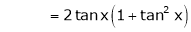
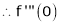
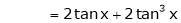
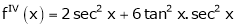

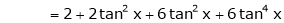

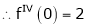
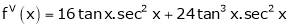
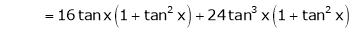
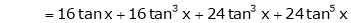
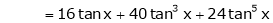
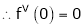

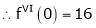
 By equation (1)
By equation (1)
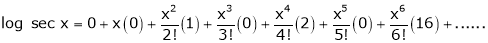
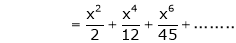
Q14) Expand  upto x6
upto x6
A14)
Here 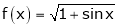
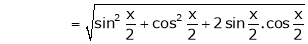
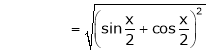

Now we know that
 … (1)
… (1)
 … (2)
… (2)
Adding (1) and (2) we get
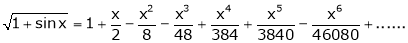
Q15) Expand 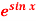 by using Maclaurin’s series.
by using Maclaurin’s series.
A15)
Let


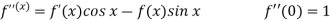
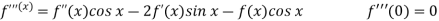
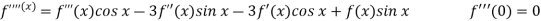
Put these values in Maclaurin’s series-

Or
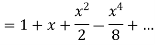
Q16) Expand  in power of (x – 3)
in power of (x – 3)
A16)
Let 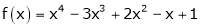
Here a = 3
Now by Taylor’s series expansion,
 … (1)
… (1)
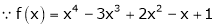

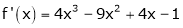

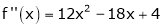
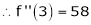
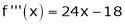
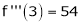
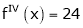
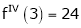
 equation (1) becomes.
equation (1) becomes.
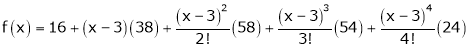
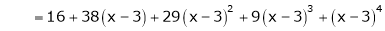
Q17) Expand  in powers of x using Taylor’s theorem,
in powers of x using Taylor’s theorem,
A17)
Here
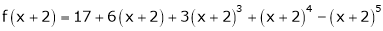
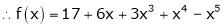
i.e. 
Here
h = 2
 By Taylors series
By Taylors series
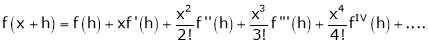 … (1)
… (1)

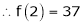
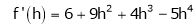

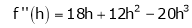


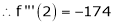


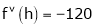
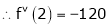
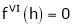

 By equation (1)
By equation (1)
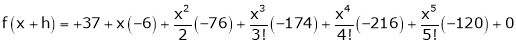
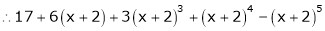
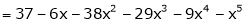
Q18) Find the value of 5 , correct to five decimal places by using the power series for
, correct to five decimal places by using the power series for  .
.
A18)
As we know that the exponential series is-
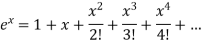

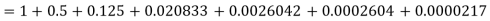
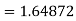
Here we get-
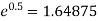
Now
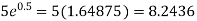
Q19) Expand 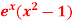 as far as the term in
as far as the term in  .
.
A19)
We know that the power series for  is-
is-
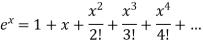
Here we have to find- 
So that-
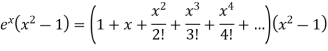
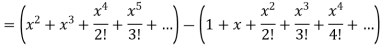
On solving, we get-