Unit - 2
Riemann integration
Q1) Define partition
A1)
Suppose [a, b] be a closed interval.
The partition of [a, b] means a finite set P of points  where
where

The partition P consists of n+1 points.
Q2) What are supremum and infimum?
A2)
The i’th sub interval is denoted by 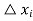

Let f be a bounded real function on [a, b].
Evidentally f is bounded on each sub-interval corresponding to each partition P,
 be the supremum and infimumof f in
be the supremum and infimumof f in  .
.
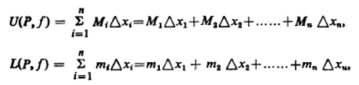
These are called the upper and lower sums of f corresponding to the partition P.
Q3) Define lower Riemann integral and upper Riemann integral.
A3)
The lower Riemann integral of f on [a, b] is defined as Sup {L(P, f) | P is a partition of [a, b]} and is defined by
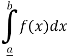
i.e.
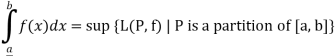
The upper Riemann integral of f on [a, b] is defined as Sup {U(P, f) | P is a partition of [a, b]} and is defined by

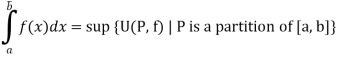
Q4) What do you understand by Riemann integrability?
A4)
A bounded function f: [a, b] 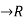 is said to be “Riemann integrable” over [a, b] if
is said to be “Riemann integrable” over [a, b] if

And it is denoted by 
Note-
- If f: [a, b]
 is a bounded function, then
is a bounded function, then
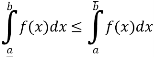
2. A bounded function f is Riemann integrable on [a, b]
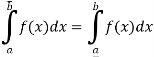
3. If bounded function f is such that
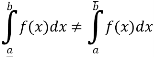
Then f is not Riemann integrable on [a, b].
Q5) A constant function is Riemann integrable on [a, b].
A5)
Let f(x) = k for every x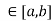 , where
, where 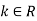 be a constant.
be a constant.
Clearly f is bounded on [a, b] and inf f = sup f = k
Let  be a partition on [a, b].
be a partition on [a, b].
Let 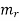 and
and 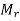 be the inf and sup of f on
be the inf and sup of f on  , where
, where 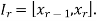
Since f(x) = k for every x
 =
= 
So that
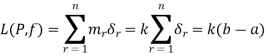
And
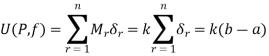
Hence

Similarly
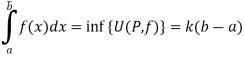
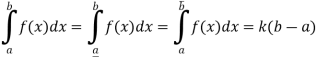
So that f is Riemann integrable on [a, b].
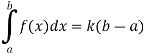
Q6) Show that the function f defined by

Is not integrable on any interval.
A6)
Suppose we consider a partition P of an interval [a, b].
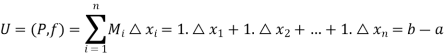
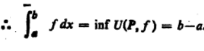

= sup{ }
}
= 0
Thus
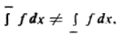
Q7) Give the necessary condition for Riemann integrability.
A7)
The bounded function f is integrable,
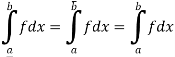
Let 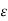 be any positive number.
be any positive number.
By the Darboux’s theorem there exists 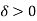 such that for every partition P with norm
such that for every partition P with norm 

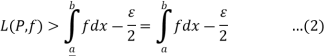
Or
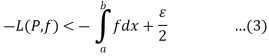
From (1) and (3), we get on adding,
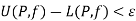
For every partition P with norm 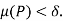
Q8) What is the sufficient condition for Riemann integrability.
A8)
Let  be any positive number. For any partition P with norm
be any positive number. For any partition P with norm  , where
, where
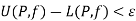
Also for any partition P. We know that-
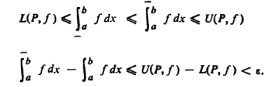
Since 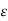 is an arbitrary positive number, so that we see that a non-negative number is less than every positive number, so that it must be equal to zero.
is an arbitrary positive number, so that we see that a non-negative number is less than every positive number, so that it must be equal to zero.
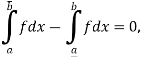
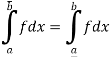
So that f is integrable.
Q9) Prove that f(x) = 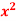 is integrable on [0, a] and
is integrable on [0, a] and 
A9)
f(x) =  is bounded on [0, a].
is bounded on [0, a].
Let us consider the partition P = {0, a/n, 2a/n,….,ra/n,…,na/n}
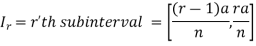
Length of each sub-interval = 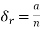
Since f(x) =  is increasing function in [0, a],
is increasing function in [0, a],
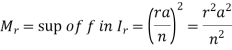
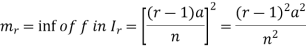
So that
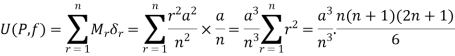
And
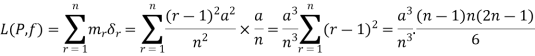
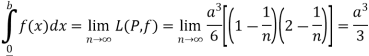
And
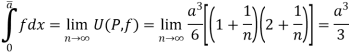
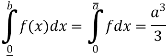
f(x) =  is integrable on [0, a] and
is integrable on [0, a] and 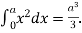
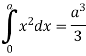
Q10) if  and
and  are two bounded and integrable functions on [a, b] then f =
are two bounded and integrable functions on [a, b] then f =  is also integrable on [a, b] and
is also integrable on [a, b] and
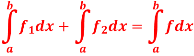
A10)
Here f is bounded on [a, b].
Suppose 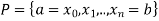 be any partition of [a, b] and
be any partition of [a, b] and 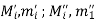 ;
;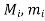 be the bounds of
be the bounds of 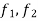 and f respectively in
and f respectively in 
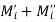 and
and  are the rough upper and lower bounds whereas
are the rough upper and lower bounds whereas  and
and  are the supremum and infimum of of f in
are the supremum and infimum of of f in 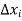 .
.
So that
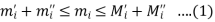
Multiply by  and adding all these inequalities for i = 1, 2, 3,…,n, we obtain
and adding all these inequalities for i = 1, 2, 3,…,n, we obtain
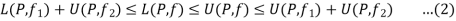
Suppose 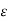 be a positive number.
be a positive number.
Since 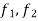 are integrable therefore we can choose
are integrable therefore we can choose 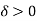 such that for any partitions P with norm
such that for any partitions P with norm 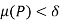 we have
we have
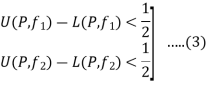
Thus for any partition P with norm  , we have, from equation (2) and (3)
, we have, from equation (2) and (3)
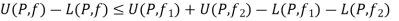
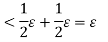
Thus the function f is integrable.
Since  are integrable and
are integrable and 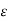 is any positive number, therefore by using Darboux’s theorem, for every
is any positive number, therefore by using Darboux’s theorem, for every  such that for all partitions P whose norm
such that for all partitions P whose norm 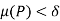 , we have
, we have
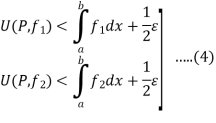
Also
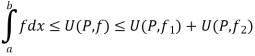
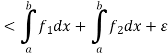
Since 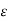 is arbitrary,
is arbitrary,
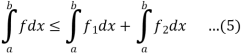
Proceeding with  in place of
in place of  respectively, we get
respectively, we get
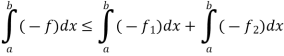
Or
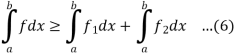
From equation (5) and (6)
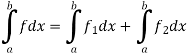
Q11) if  and
and 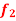 are two bounded and integrable functions on [a, b] then f =
are two bounded and integrable functions on [a, b] then f =  is also integrable on [a, b] and
is also integrable on [a, b] and
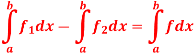
A11)
Let f = 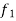 +
+ 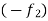 so that f is bounded on [a, b].
so that f is bounded on [a, b].
Suppose  be any partition of [a, b] and
be any partition of [a, b] and  ;
; be the bounds of
be the bounds of 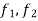 and f respectively in
and f respectively in 
The bounds of
So that  are
are 
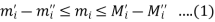
Multiply by  and adding all these inequalities for i = 1, 2, 3,…,n, we obtain
and adding all these inequalities for i = 1, 2, 3,…,n, we obtain
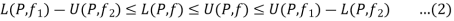
Suppose 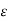 be a positive number.
be a positive number.
Since  are integrable therefore we can choose
are integrable therefore we can choose  such that for any partitions P with norm
such that for any partitions P with norm  we have
we have
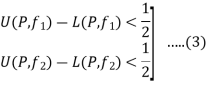
Thus for any partition P with norm  , we have, from equation (2) and (3)
, we have, from equation (2) and (3)
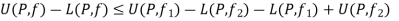
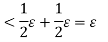
Thus the function f is integrable.
Since  are integrable and
are integrable and  is any positive number, therefore by using Darboux’s theorem, for every
is any positive number, therefore by using Darboux’s theorem, for every  such that for all partitions P whose norm
such that for all partitions P whose norm 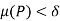 , we have
, we have
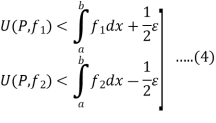
Also
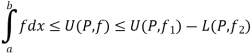
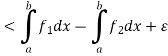
Since  is arbitrary,
is arbitrary,

Proceeding with  in place of
in place of  respectively, we get
respectively, we get
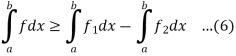
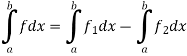
Q12) What do you understand by equivalency of two definitions of integration?
A12)
We have two definitions of integrability, now we will show the equivalency of these two definitions.
Suppose f is the bounded function and integrable, so that
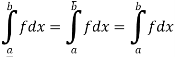
Suppose  be any positive number.
be any positive number.
By using Darboux’s theorem, there exists  such that for every partition P with norm
such that for every partition P with norm  ,
,
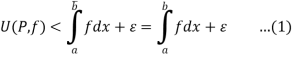
And
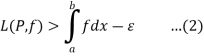
If 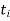 is any point of
is any point of  , we have
, we have
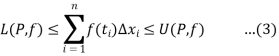
From (1), (2) and (3), we obtain that for any  , such that for every partition with norm
, such that for every partition with norm  ,
,
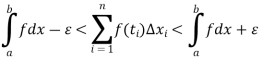
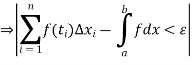
Thus the function is integrable according to the second definition also.
Q13) If the functions 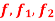 where
where  are bounded and integrable on [a, b], then
are bounded and integrable on [a, b], then
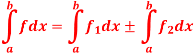
A13)
Let  be any positive number and
be any positive number and 
Since 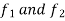 are integrable, therefore for every
are integrable, therefore for every 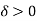 such that for every partition
such that for every partition  with norm
with norm  and for every choice of points
and for every choice of points  in
in  ,
,
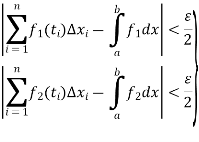
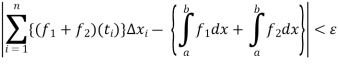
Thus
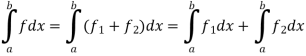
Similarly we can prove for 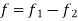 .
.
Q14) Prove that every monotonic function is integrable.
A14)
We will prove the theorem for the case where I: [a,b] 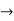 R is a monotonically increasing function. The function is bounded. f(a) and f(b) being g.l.b. And l.u.b. Let Î > 0 be given number, Let n be a positive integer such that
R is a monotonically increasing function. The function is bounded. f(a) and f(b) being g.l.b. And l.u.b. Let Î > 0 be given number, Let n be a positive integer such that
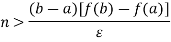
Divide the interval [a,b] into n equal sub-intervals, by the partition P = 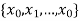 of [a, b]. Then
of [a, b]. Then
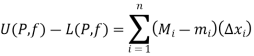
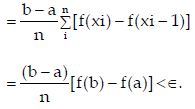
This proves that f is integrable.
Q15) Prove that every continuous function is integrable.
A15)
Here we will prove that a function f which is continuous on [a, b] is also integrable on [a, b].
Suppose 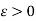 be given
be given
Let we choose a positive number 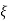 , such that
, such that
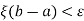
Since f is continuous on [a, b], therefore it is bounded and is uniformly continuous on [a, b].
 , such that
, such that
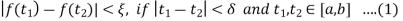
Now choose a partition P with norm 
Then by equation (1), we get
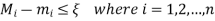
Hence
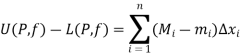
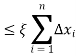
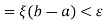
Thus f is integrable.
Q16) if f and g are integrable on [a, b], then so is f + g, and
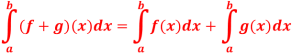
A16)
Any Riemann sum of f+g over a partition P =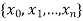 of [a, b]can
of [a, b]can
Be written as
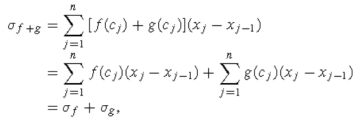
Here  are the Riemann sums for f and g.
are the Riemann sums for f and g.
Above definition(property), implies that if  > 0 there are positive numbers
> 0 there are positive numbers 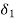 and
and  such that
such that

So the conclusion follows from the above definition.
Q17) If f and g are integrable on [a, b] and 
Then
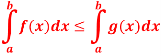
A17)
Since 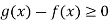 , every lower sum of g – f over any partition of [a, b] is non-negative, therefore,
, every lower sum of g – f over any partition of [a, b] is non-negative, therefore,
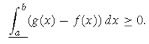
Hence
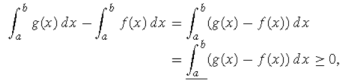
Q18) What do you understand by monotone function.
A18)
A function f is monotone increasing on (a, b) if f(x) 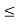 f(y) whenever x < y. A function f is monotone decreasing on (a, b) if f(x)
f(y) whenever x < y. A function f is monotone decreasing on (a, b) if f(x)  f(y) whenever x < y.
f(y) whenever x < y.
A function f is called monotone on (a, b) if it is either always monotone increasing or monotone decreasing.
Note-
- If f is a monotonic function defined on an interval I, then f is differentiable almost everywhere on I, i.e. the set of numbers x in I such that f is not differentiable in x has Lebesgue measure zero.
- If f is a monotonic function defined on an interval [a, b], then f is Riemann integrable.
- A function is unimodal if it is monotonically increasing up to some point (the mode) and then monotonically decreasing.
Q19) State and prove intermediate value theorem.
A19)
Statement-
Let f be a continuous function on an interval containing a and b. If K is any number between f(a) and f(b) then there is a number c, a  c S b such that f(c) = K
c S b such that f(c) = K
Proof:
Either f(a) = f(b) or f(a) < f(b) or f(b) < f(a). If f(a) = f(b) then K = f(a) = f(b) and so c can be taken to be either a or b. We will assume that f(a) < f(b). (The other case can be dealt with similarly.) We can, therefore, assume that f(a) < K < f(b).
Let S denote the collection of all real numbers x in [a, b] such that f(x) < K. Clearly S contains a, so S 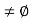 and b is an upper bound for S. Hence, by completeness property of R, S has least upper bound and let us denote this least upper bound by c. Then a
and b is an upper bound for S. Hence, by completeness property of R, S has least upper bound and let us denote this least upper bound by c. Then a  c
c 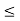 b. We want to show that f(c) = K. Let S denote the collection of all real numbers x in [a, b] such that f(x) < K. Clearly S contains a, so S
b. We want to show that f(c) = K. Let S denote the collection of all real numbers x in [a, b] such that f(x) < K. Clearly S contains a, so S 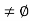 and b is an upper bound for S. Hence, by completeness property of R, S has least upper bound and let us denote this least upper bound by c. Then a
and b is an upper bound for S. Hence, by completeness property of R, S has least upper bound and let us denote this least upper bound by c. Then a  c
c  b. We want to show that f(c) = K.
b. We want to show that f(c) = K.
Since f is continuous on [a, b], f is continuous at c. Therefore, given  > 0, there exists a 6 > 0 such that whenever x is in [a, b] and |x – c| < 6, |f(x) – f(c) ( < G,
> 0, there exists a 6 > 0 such that whenever x is in [a, b] and |x – c| < 6, |f(x) – f(c) ( < G,
i.e., f(c) –  < f(x) < f(c) +
< f(x) < f(c) +  .
.
If c  b, we can clearly assume that c + 6 < b. Now c is the least upper bound of S. So c –
b, we can clearly assume that c + 6 < b. Now c is the least upper bound of S. So c –  is not ‘an upper bound’ of S. Hence, there exists a y in S such that c – 6 < y
is not ‘an upper bound’ of S. Hence, there exists a y in S such that c – 6 < y 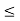 c. Clearly |y – c| <
c. Clearly |y – c| < 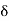 and so by (4) above, we have
and so by (4) above, we have
f(c) – 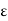 < f(y) < f(c) +
< f(y) < f(c) +  .
.
Since y is in S, therefore f(y) < K. Thus, we get
f(c) – S < K
If now c = b then K –  < K < f(b) = f(c), i.e., K < f(c) + E. If c
< K < f(b) = f(c), i.e., K < f(c) + E. If c  b, then c < b; then there exists an x such that c < x < c + 6, 6, x
b, then c < b; then there exists an x such that c < x < c + 6, 6, x 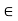 [a, b] and for this x, f(x) < f(c) +
[a, b] and for this x, f(x) < f(c) + 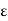 by (4) above. Since x > c, K
by (4) above. Since x > c, K 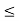 f(x), for otherwise x would be in S which will imply that c is not an upper bound of S. Thus, again we have K
f(x), for otherwise x would be in S which will imply that c is not an upper bound of S. Thus, again we have K  f(x) < f(c) + E.
f(x) < f(c) + E.
In any case,
K < f(c) +  ...(6)
...(6)
Combining (5) and (6), we get for every 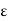 > 0
> 0
f (c) – 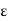 < K < f(c) +
< K < f(c) + 
Which proves that K = f(c), since 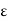 is arbitrary while K, f(c) are fixed. In fact, when f(a) < K < f(b)
is arbitrary while K, f(c) are fixed. In fact, when f(a) < K < f(b)
And f(c) = K, then a < c < b.