Unit - 2
Rate of convergence of the above methods
Q1) What is the rate of convergence for bisection and Regula-falsi method?
A1)
Bisection Mehtod: The percentage error 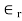 defined by
defined by

The rate of convergence for bisection method is 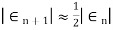
i.e. it converges linearly.
Regula-Falsi Method: The rate of convergence is
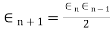

Here p=1.618 and is linear.
Q2) Apply Gauss Elimination method to solve the equations)
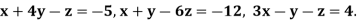
A2)
Given Check Sum (sum of coefficient and constant)
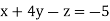 -1 …. (I)
-1 …. (I)
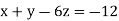 -16 …. (ii)
-16 …. (ii)
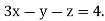 5 …. (iii)
5 …. (iii)
(I)We eliminate x from (ii) and (iii)
Apply eq(ii)-eq(i) and eq(iii)-3eq(i) we get
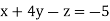 -1 ….(i)
-1 ….(i)
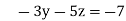 -15 ….(iv)
-15 ….(iv)
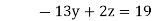 8 ….(v)
8 ….(v)
(II) We eliminate y from eq(v)
Apply 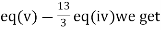
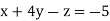 -1 ….(i)
-1 ….(i)
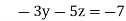 -15 ….(iv)
-15 ….(iv)
 73 ….(vi)
73 ….(vi)
(III) Back Substitution we get
From (vi) we get 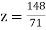
From (iv) we get 
From (i) we get 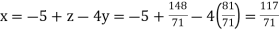
Hence the solution of the given equation is 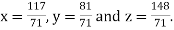
Q3) Solve the equation by Gauss Elimination Method)
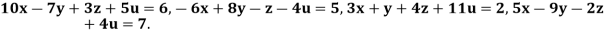
A3)
Given 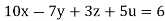
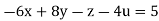
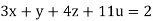

Rewrite the given equation as
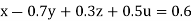 … (i)
… (i)
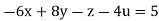 ….(ii)
….(ii)
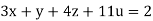 ….(iii)
….(iii)
 …(iv)
…(iv)
(I) We eliminate x from (ii),(iii) and (iv) we get
Apply eq(ii) + 6eq(i), eq(iii) -3eq(i), eq(iv)-5eq(i) we get
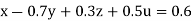 …(i)
…(i)
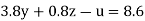 ….(v)
….(v)
 ….(vi)
….(vi)
 …(vii)
…(vii)
(II) We eliminate y from (vi) and (vii) we get
Apply 3.8 eq(vi)-3.1eq(v) and 3.8eq(vii)+5.5eq(v) we get
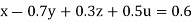 …(i)
…(i)
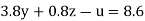 ….(v)
….(v)
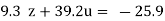 …(viii)
…(viii)
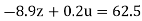 …(ix)
…(ix)
(III) We eliminate z from eq (ix) we get
Apply 9.3eq (ix) + 8.3eq (viii), we get
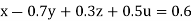 … (i)
… (i)
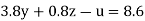 ….(v)
….(v)
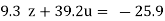 …(viii)
…(viii)
350.74u=350.74
Or u = 1
(IV) Back Substitution
From eq(viii) 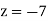
Form eq(v), we get 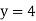
From eq(i) , 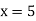
Hence the solution of the given equation is x=5, y=4, z=-7 and u=1.
Q4) Apply Gauss Elimination Method to solve the following system of equation)
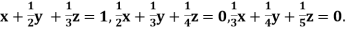
A4)
Given 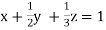 … (i)
… (i)
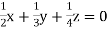 … (ii)
… (ii)
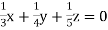 … (iii)
… (iii)
(I) We eliminate x from (ii) and (iii)
Apply 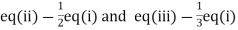 we get
we get
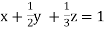 … (i)
… (i)
 … (iv)
… (iv)
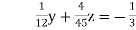 … (v)
… (v)
(II) We eliminate y from (v)
Apply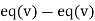 we get
we get
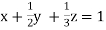 … (i)
… (i)
 … (vi)
… (vi)
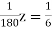 … (vii)
… (vii)
(III) Back substitution
From (vii) 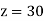
From (vi) 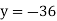
From (i) 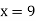
Hence the solution of the equation is 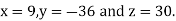
Q5) Solve the system of linear equations
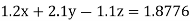

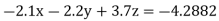
A5) Using partial pivoting by Gauss elimination method we rewrite the given equations as
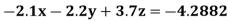 (1)
(1)
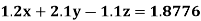 (2)
(2)
 (3)
(3)
Apply 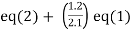 and
and 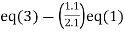
 (1)
(1)
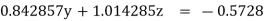 (4)
(4)
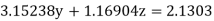 (5)
(5)
Apply 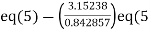 )
)
 (1)
(1)
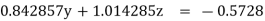 (4)
(4)
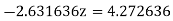
Or 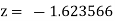 .
.
Putting value of z in 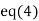 we get
we get 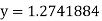 .
.
Putting values of y and z in  we get
we get 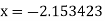 .
.
Hence the solution of the equation is  .
.
Q6) By using Gauss-Jordan method, solve the system of equations-
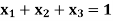
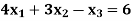
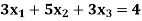
A6)
Here the augmented matrix will be-

By performing elementary row transformation, and eliminations, we get-
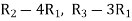

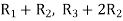

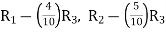
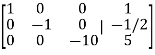
Now making the pivots as 1, ((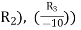
We obtain,
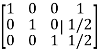
Hence the solution of the system is-
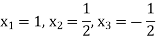
Q7) What do you understand by matrix inversion using Gauss Jordan method?
A7)
We know that X will be the inverse of a matrix A if
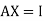
Where I is an identity matrix of order same as A.
We write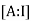 , using elementary operation we covert the matrix A in to a upper triangular matrix. Then compare this matrix with each corresponding column and using back substitution. s
, using elementary operation we covert the matrix A in to a upper triangular matrix. Then compare this matrix with each corresponding column and using back substitution. s
The determinant of this coefficient matrix is the product of the diagonal elements of the upper triangular matrix.
If this |A|=0 then inverse does not exist.
Q8) Solve the system of equations
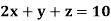
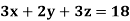
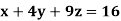
A8)
Here A =

The augmented system is

Apply 
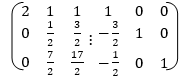
Apply 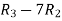
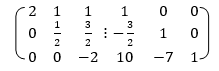
Here 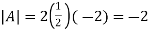
Which is non zero so the inverse exists.
Comparing the diagonal matrix with corresponding columns.
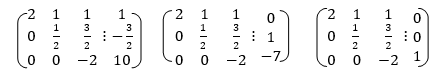
By back Substitution we get
Form first part of above 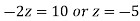

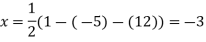
Similarly we solve second and third part and obtain a matrix whose columns are
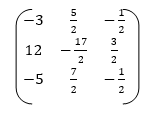
Which is the required inverse 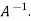
Q9) Use Jacobi’s method to solve the system of equations)
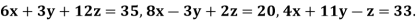
A9)
Since 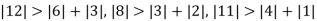
So, we express the unknown with large coefficient in terms of other coefficients.
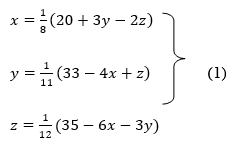
Let the initial approximation be 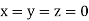
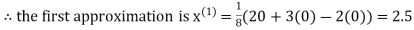

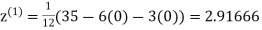
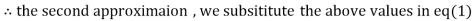
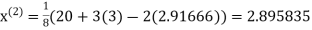
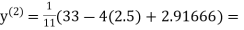 2.35606
2.35606
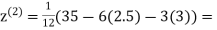 0.91666
0.91666
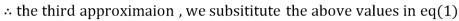
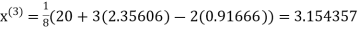
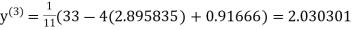
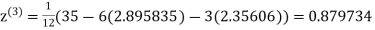
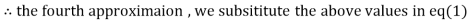
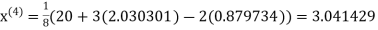
 1.932936
1.932936
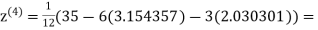 0.831912
0.831912
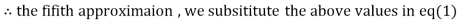
 3.016873
3.016873
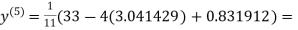 1.969654
1.969654

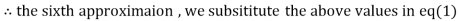
 3.010217
3.010217
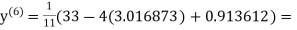 1.986010
1.986010
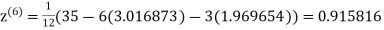
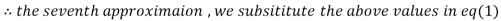
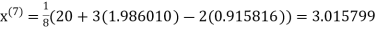
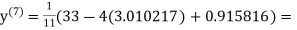 1.988631
1.988631
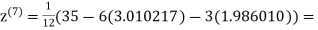 0.915055
0.915055
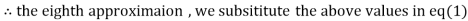

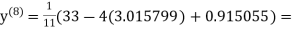 1.986532
1.986532
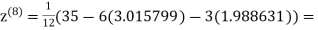 0.911609
0.911609
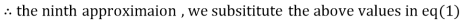
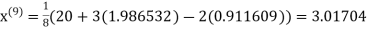
 1.985792
1.985792
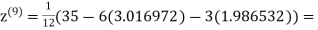 0.911547
0.911547
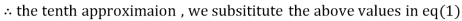
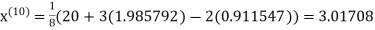
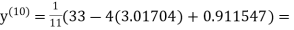 1.98576
1.98576
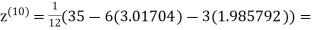 0.911698
0.911698
Since the approximation in ninth and tenth iteration is same up to three decimal places, hence the solution of the given equations is 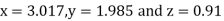
Q10) Solve by Jacobi’s Method, the equations
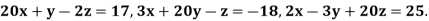
A10)
Given equation can be rewrite in the form
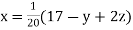 … (i)
… (i)
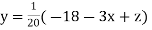 ..(ii)
..(ii)
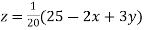 ..(iii)
..(iii)
Let the initial approximation be 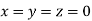

Putting these values on the right of the equation (i), (ii) and (iii) and so we get
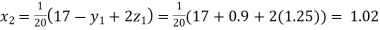
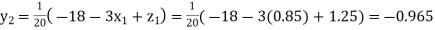
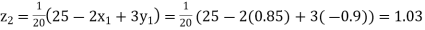
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
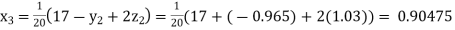
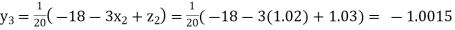
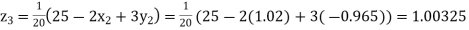
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
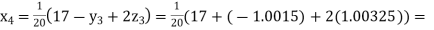 0.90025
0.90025
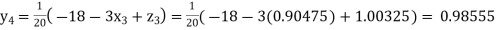
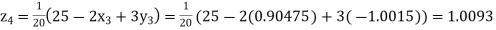
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
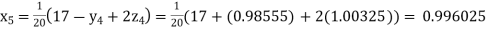
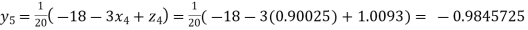
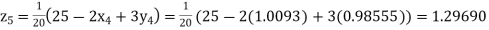
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
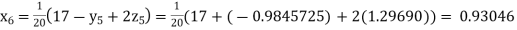
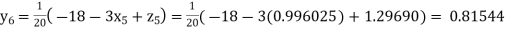
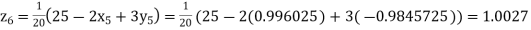
Hence solution approximately is 
Q11) Use Jacobi’s method to solve the system of the equations
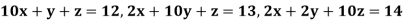
A11)
Rewrite the given equations
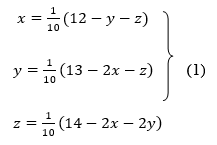
Let the initial approximation be 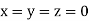
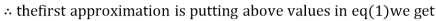
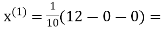 1.2
1.2
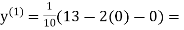 1.3
1.3


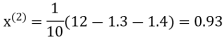
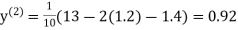
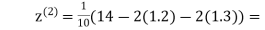 0.9
0.9
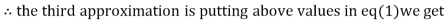


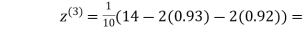 1.03
1.03

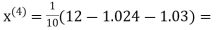 0.9946
0.9946
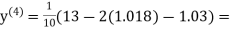 0.9934
0.9934
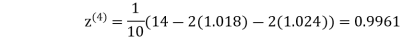
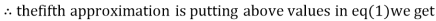
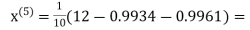 1.0015
1.0015
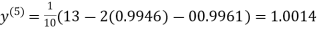

Hence the solution of the above equation correct to two decimal places is

Q12) Use Gauss –Seidel Iteration method to solve the system of equations
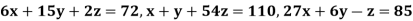
A12)
Since 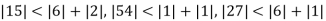
So, we express the unknown of larger coefficient in terms of the unknowns with smaller coefficients.
Rewrite the above system of equations
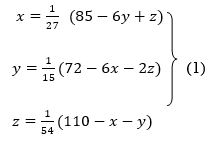
Let the initial approximation be 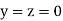
 3.14814
3.14814
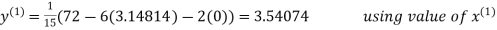
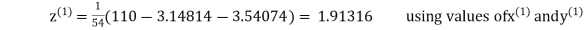

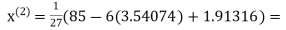 2.43217
2.43217
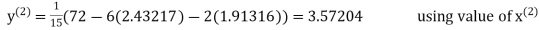

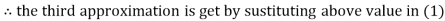
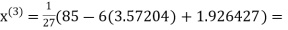 2.42571
2.42571
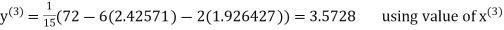
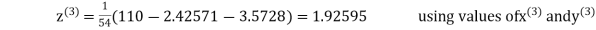
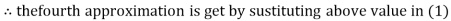
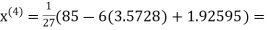 2.4260
2.4260
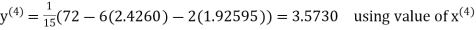
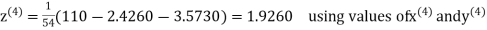
Hence the solution correct to three decimal places is
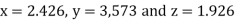
Q13) Solve the following system of equations
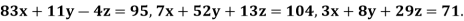 By Gauss-Seidel method.
By Gauss-Seidel method.
A13) Rewrite the given system of equations as

Let the initial approximation be 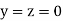
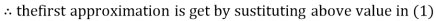
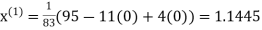
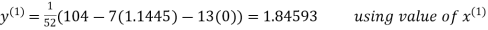


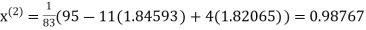
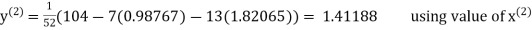
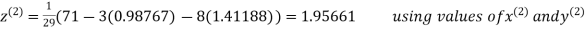
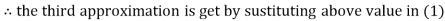

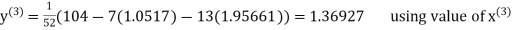
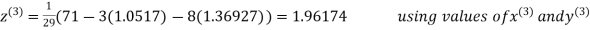
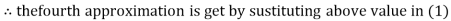
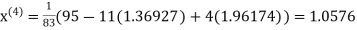


Thus the required solution is 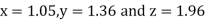
Q14) Solve the following equations by Gauss-Seidel Method
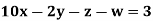
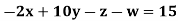
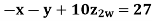
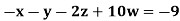
A14)
Rewrite the above system of equations
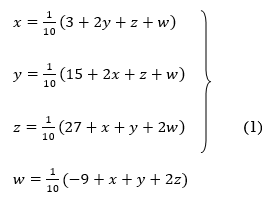
Let the initial approximation be 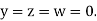
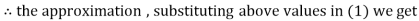
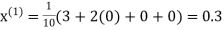

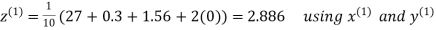


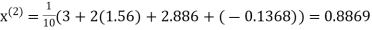
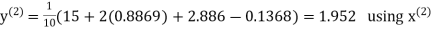
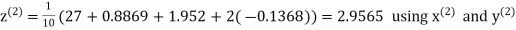
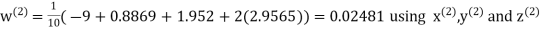

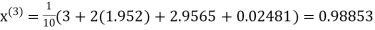
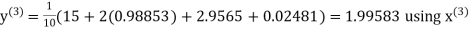
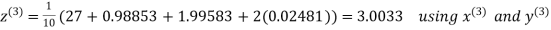
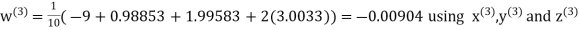

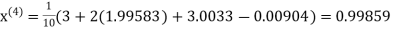
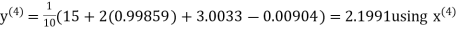
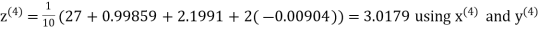
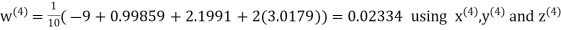

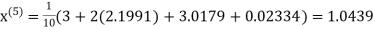
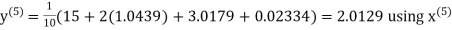
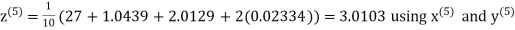
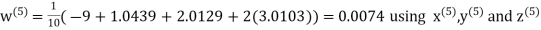
Hence the required solution is 
Q15) Explain power method.
A15)
Consider the eigen value problem
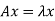
The Eigen values of a matrix A are given by the roots of the characteristic equation
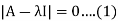
If the matrix A is of order n, then expanding the determinant, we obtain the characteristic equation as
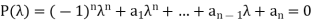
For the given matrix we write the characteristic equation, by expanding we find the roots 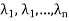 . These are called the Eigen values.
. These are called the Eigen values.
Now suppose 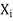 be the solution of the system of homogeneous equations, corresponding to the Eigen value
be the solution of the system of homogeneous equations, corresponding to the Eigen value 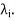
These vectors 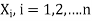 are called the Eigen vectors.
are called the Eigen vectors.
To find the approximate values of all the Eigen values and Eigen vectors, iteration method or power method is used.
Power method is used when only the largest and/or the smallest Eigen values of a matrix are desired.
Q16) Find the largest Eigen value and the corresponding Eigen vector of the matrix 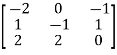
Also find the error in the value of the largest Eigen value.
A16)
Let us choose the initial vector
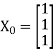
Then
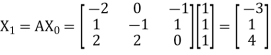
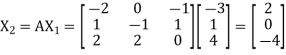

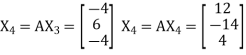
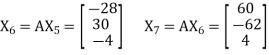
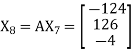 and
and 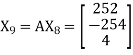
Now put 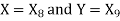 , then-
, then-
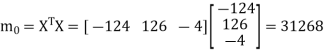
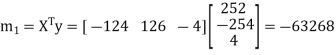

Hence the largest Eigen value is-
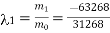
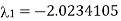
And the corresponding Eigen vector is-
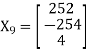
The error can be calculated as-
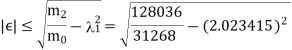
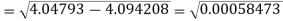
Q17) Give the steps used in power method.
A17)
Step-1: First we choose an arbitrary real vector 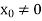 , basically
, basically 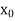 is chosen as-
is chosen as-

Step-2: Compute 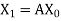 ,
, 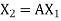 ,
,  ,
, 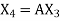 , …………
, …………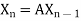 Put
Put 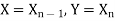
Step-3: Compute  ,
,  ,
, 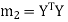
Step-4: The largest Eigen value is
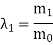
The error in 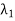 can be find as-
can be find as-
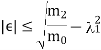
The Eigen vector corresponding to 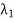 is
is 