Unit - 4
Numerical Integration
Q1) What is Newton cote’s formula.
A1)
Suppose  where y takes the values
where y takes the values 
And let the integration interval (a,b) is divided into n equal sub-intervals, each of width h = b – a /n, so that,
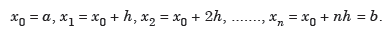
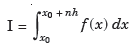

The above formula is known as Newton’s cotes formula.
This is also known as general Quadrature formula.
Q2) State the trapezoidal rule for finding an approximate area under the given curve. A curve is given by the points (x, y) given below:
(0, 23), (0.5, 19), (1.0, 14), (1.5, 11), (2.0, 12.5), (2.5, 16), (3.0, 19), (3.5, 20), (4.0, 20).
Estimate the area bounded by the curve, the x axis and the extreme ordinates.
A2)
We construct the data table:
X | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
Y | 23 | 19 | 14 | 11 | 12.5 | 16 | 19 | 20 | 20 |
Here length of interval h =0.5, initial value a = 0 and final value b = 4
By Trapezoidal method
Area of curve bounded on x axis =

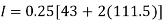
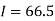
Q3) Compute the value of 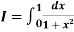
A3)
Using the trapezoidal rule with h=0.5, 0.25 and 0.125.
Here 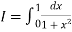
For h=0.5, we construct the data table:
X | 0 | 0.5 | 1 |
Y | 1 | 0.8 | 0.5 |
By Trapezoidal rule
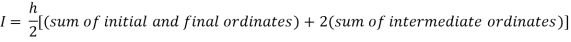
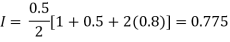
For h=0.25, we construct the data table:
X | 0 | 0.25 | 0.5 | 0.75 | 1 |
Y | 1 | 0.94117 | 0.8 | 0.64 | 0.5 |
By Trapezoidal rule
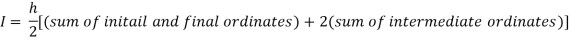
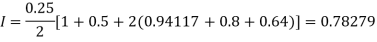
For h = 0.125, we construct the data table:
X | 0 | 0.125 | 0.25 | 0.375 | 0.5 | 0.625 | 0.75 | 0.875 | 1 |
Y | 1 | 0.98461 | 0.94117 | 0.87671 | 0.8 | 0.71910 | 0.64 | 0.56637 | 0.5 |
By Trapezoidal rule
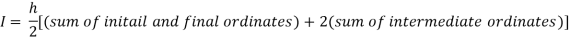
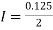 [(1+0.5)+2(0.98461+0.94117+0.87671+0.8+0.71910+0.64+0.56637)]
[(1+0.5)+2(0.98461+0.94117+0.87671+0.8+0.71910+0.64+0.56637)]
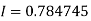
Q4) Evaluate using trapezoidal rule with five ordinates
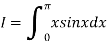
A4)
Here 
We construct the data table:
X | 0 |  |  | 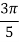 | 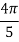 | 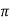 |
Y | 0 | 0.3693161 | 1.195328 | 1.7926992 | 1.477265 | 0 |
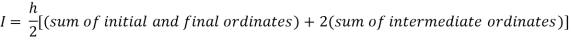
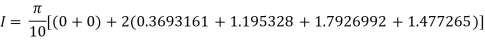
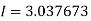
Q5) Explain Simpson’s one-third rule.
A5)
Let the interval [a,b] be divided into n equal intervals such that 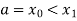 <
< <….<
<….< =b.
=b.
Here 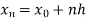 .
.
To find the value of 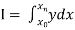 .
.
Setting n = 2,
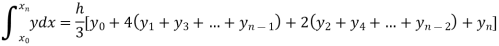
Which is known as Simpson’s 1/3- rule or Simpson’s rule.
Q6) Estimate the value of the integral
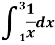
A6)
By Simpson’s rule with 4 strips and 8 strips respectively.
For n=4, we have 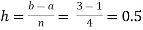
E construct the data table:
X | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
Y=1/x | 1 | 0.66666 | 0.5 | 0.4 | 0.33333 |
By Simpson’s Rule
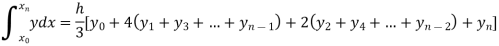
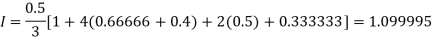
For n = 8, we have 
X | 1 | 1.25 | 1.50 | 1.75 | 2.0 | 2.25 | 2.50 | 2.75 | 3.0 |
Y=1/x | 1 | 0.8 | 0.66666 | 0.571428 | 0.5 | 0.444444 | 0.4 | 0.3636363 | 0.333333 |
By Simpson’s Rule

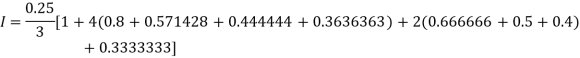
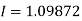
Q7) Evaluate 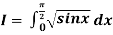 Using Simpson’s 1/3 rule with
Using Simpson’s 1/3 rule with 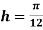 .
.
A7)
For  , we construct the data table:
, we construct the data table:
X | 0 | 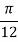 |  |  |  | 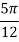 |  |
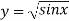 | 0 | 0.50874 | 0.707106 | 0.840896 | 0.930604 | 0.98281 | 1 |
By Simpson’s Rule
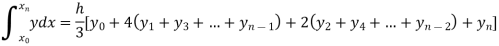
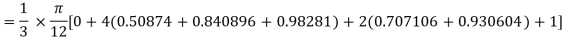
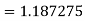
Q8) Using Simpson’s 1/3 rule with h = 1, evaluate
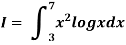
A8)
For h = 1, we construct the data table:
X | 3 | 4 | 5 | 6 | 7 |
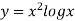 | 9.88751 | 22.108709 | 40.23594 | 64.503340 | 95.34959 |
By Simpson’s Rule
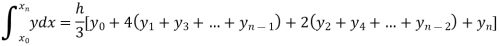
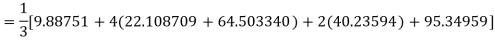
= 177.3853
Q9) Evaluate 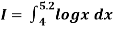
A9)
By Simpson’s 3/8 rule.
Let us divide the range of the interval [4, 5.2] into six equal parts.

For h=0.2, we construct the data table:
X | 4.0 | 4.2 | 4. 4 | 4.6 | 4.8 | 5.0 | 5.2 |
Y=logx | 1.3863 | 1.4351 | 1.4816 | 1.5261 | 1.5686 | 1.6094 | 1.6487 |
By Simpson’s 3/8 rule
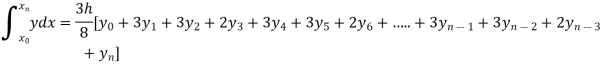

= 1.8278475
Q10) Evaluate 
A10)
Let us divide the range of the interval [0,6] into six equal parts.
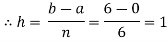
For h=1, we construct the data table:
X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
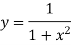 | 1 | 0.5 | 0.2 | 0.1 | 0.0588 | 0.0385 | 0.027 |
By Simpson’s 3/8 rule
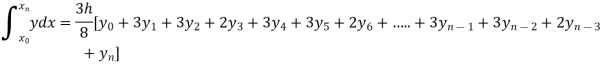
 +3(0.0385)+0.027]
+3(0.0385)+0.027]
=1.3571
Q11) Evaluate 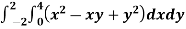
A11)
Let 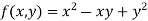
Here the interval of x and y are 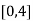 and
and 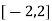 .
.
Let 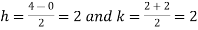
Consider the following table:
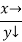 |
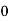 |
 |
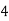 |
 |
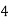
|
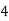 |
 |
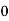 |
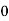 |
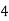 |
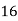 |
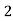 |
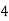 |
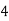 |
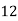 |

By Trapezoidal Rule
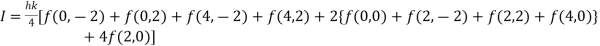
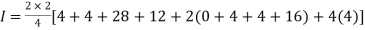
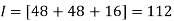 .
.
Q12) Evaluate 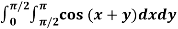
A12)
Let 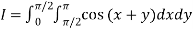
And 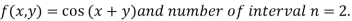
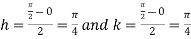
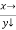 |
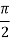 |
 |
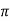 |
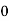 |
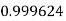 |
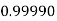 |
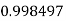 |
 |
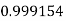 |
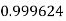 |
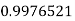 |
 |
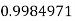 |
 |
 |
By Simpson’s 1/3 Rule
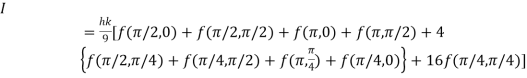

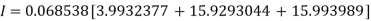
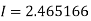
Q13) Given that
X | 1.0 | 1.1 | 1.2 | 1.3 |
Y | 0.841 | 0.891 | 0.932 | 0.963 |
Find 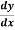 at
at 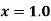 .
.
A13)
Here the first derivative is to be calculated at the beginning of the table, therefore forward difference formula will be used
Forward difference table is given below:
X | Y |  | 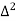 | 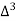 |
1.0
1.1
1.2
1.3 | 0.841
0.891
0.932
0.962 |
0.050
0.041
0.031 |
-0.009
-0.010 |
-0.001 |
By Newton’s forward differentiation formula for differentiation
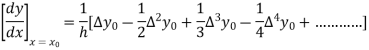
Here 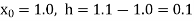
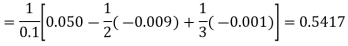
Q14) Find the first and second derivatives of the function given below at the point 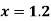 :
:
X | 1 | 2 | 3 | 4 | 5 |
Y | 0 | 1 | 5 | 6 | 8 |
A14)
Here the point of the calculation 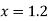 is at the beginning of the table,
is at the beginning of the table,
Forward difference table is given by:
X | Y | 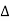 | 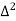 |  |  |
1
2
3
4
5 | 0
1
5
6
8 |
1
4
1
2 |
3
-3
1 |
-6
4
|
-10
|
By Newton’s forward differentiation formula for differentiation
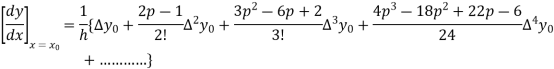
Here 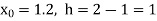 ,
,  0.
0.
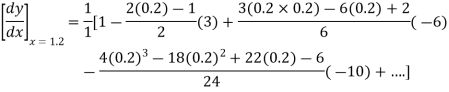
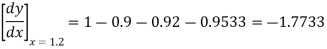
Again
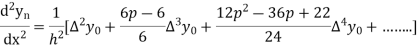
At 

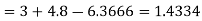
Q15) From the following table of values of x and y find 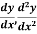 for
for 
X | 1.00 | 1.05 | 1.10 | 1.15 | 1.20 | 1.25 | 1.30 |
Y | 1.0000 | 1.02470 | 1.04881 | 1.07238 | 1.09544 | 1.11803 | 1.14017 |
A15)
Here the value of the derivative is to be calculated at the beginning of the table.
Forward difference table is given by
X | Y | 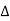 |  | 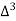 |  | 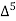 | 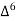 |
1.00
1.05
1.10
1.15
1.20
1.25
1.30 | 1.0000
1.02470
1.04881
1.07238
1.09544
1.11803
1.14017 |
0.02470
0.02411
0.02357
0.02306
0.02259
0.02214 |
-0.00059
-0.00054
-0.00051
-0.00047
-0.00045 |
0.00005
0.00003
0.00004
0.00002 |
-0.00002
0.00001
-0.00002 |
0.00003
-0.00003 |
-0.00006 |
From Newton’s forward difference formula for differentiation we get
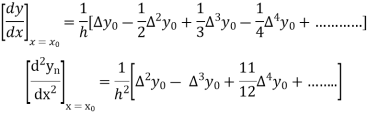
Here 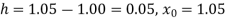
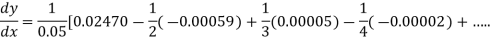
=0.48763

Q16) Given that
X | 0.1 | 0.2 | 0.3 | 0..4 |
Y | 1.10517 | 1.22140 | 1.34986 | 1.49182 |
Find 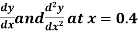 ?
?
A16)
Backward difference table:
X | Y |  | 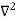 |  |
0.1
0.2
0.3
0.4 | 1.10517
1.22140
1.34986
1.49182 |
0.11623
0.12846
0.14196 |
0.01223
0.01350 |
0.00127 |
Newton’s Backward formula for differentiation
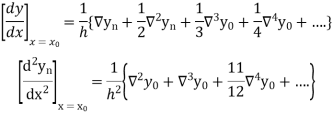
Here 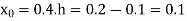
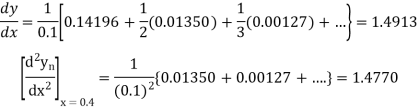
Q17) Given that
X | 1.0 | 1.2 | 1.4 | 1.6 | 1.8 | 2.0 |
Y | 0 | 0.128 | 0.544 | 1.296 | 2.432 | 4.0 |
Find the derivative of y at 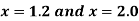 ?
?
A17)
The difference table is given below:
X | Y |  |  | 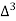 | 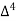 |
1.0
1.2
1.4
1.6
1.8
2.0 | 0
0.128
0.544
1.296
2.432
4.0 |
0.128
0.416
0.752
0.136
1.568
|
0.288
0.336
0.384
0.432 |
0.048
0.048
0.048 |
0
0 |
Since the point  is at the beginning of the table therefore
is at the beginning of the table therefore
From Newton’s forward difference formula for differentiation we get

Here 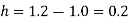
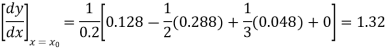
Since the point is at the end of the table therefore
is at the end of the table therefore
Backward difference table is:
X | Y |  |  |  |  |
1.0
1.2
1.4
1.6
1.8
2.0 | 0
0.128
0.544
1.296
2.432
4.000 |
0.128
0.416
0.752
0.136
1.568 |
0.288
0.336
0.384
0.432 |
0.048
0.048
0.048 |
0
0 |
Newton’s Backward formula for differentiation
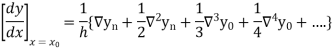

Q18) Explain Newton’s backward difference formula.
A18)
This method is useful for interpolation near the ending of a set of tabular values.
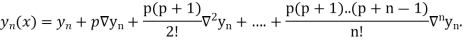
Where 
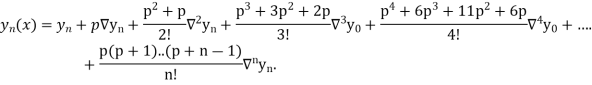
Differentiating both side with respect to p, we get
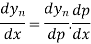

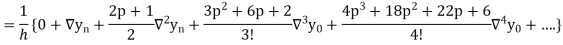
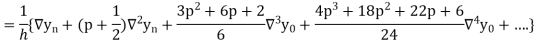
This formula is applicable to compute the value of  for non tabular values of x.
for non tabular values of x.
For tabular values of x , we can get formula by putting 
Therefore
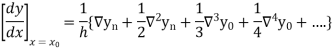
In similar manner we can get the formula for higher order by differentiating the previous order formulas
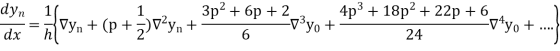
Differentiating both side with respect to p, we get
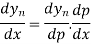

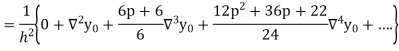
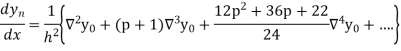
Also

Q19) Explain Newton’s forward difference formula.
A19)
This method is useful for interpolation near the beginning of a set of tabular values.

Where 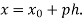
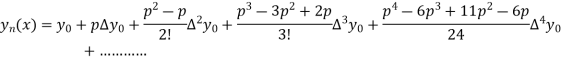
Differentiating both side with respect to p, we get
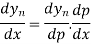
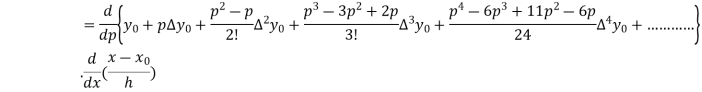
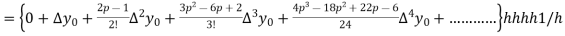 h
h
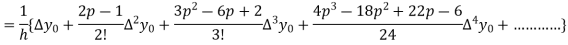
This formula is applicable to compute the value of 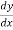 for non tabular values of x.
for non tabular values of x.
For tabular values of x , we can get formula by putting 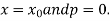
Therefore
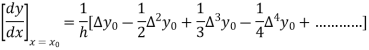
In similar manner we can get the formula for higher order by differentiating the previous order formulas
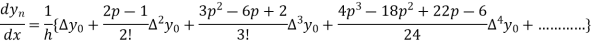
Again differentiating with respect to p, we get
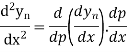
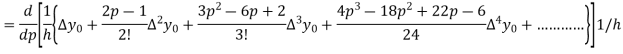
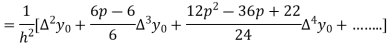
Hence
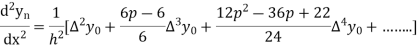
Also
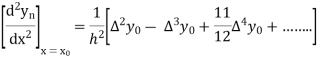
And so on.