Unit - 1

Definition and examples of rings

Q1) Define rings with help of examples.

A1)

Looking at the common features of the examples discussed in the last section suggests:

Definition

A ring is a set R plus a pair of binary operations + and. It satisfies the following axioms:

1. Under the operation +, R is an abelian group.

2. The operation is associative in nature (and it is of course closed also),

1. Under addition and multiplication modulo n, the numbers modulo n: Zn form a commutative ring with identity. This is a finite ring with the components 0, 1,..., n - 1, and the elements a that are coprime to n are invertible.

2. Under the right addition and multiplication, the sets Q, R, and C are all commutative rings with identity. Every non-zero element has an inverse in these.

3. The quaternions H = a + ib + jc + kd | a, b, c, d R stated in the previous section create a non-commutative ring with identity when added and multiplied according to the following rules:

i2 = j2 = k2 = i j k = -1.

In fact one can find an inverse for any non-zero quaternion using the trick:

(a + ib + jc + kd)(a - ib - jc - kd) = a2 + b2 + c2 + d2

As in the similar method for finding the inverse of a complex number.

4. Under standard matrix addition and multiplication, the set of all 2 2 real matrices forms a ring.

This is an identity ring that is non-commutative

.

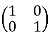In fact, the set of n × n matrices with entries in any ring forms a ring.

5. We can specify a finite ring by providing addition and multiplication tables, just as we can express a finite group by providing its multiplication table.

R = 0, a, b, c, for example, with tables

+	0		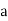b	c		.	0		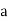b	c
0	0		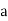b	c		0	0	0	0	0
a	a	0	c	b		a	0	0	a	a
b	b	c	0	a		b	0	0	b	b
c	c	b	a	0		c	0	0	c	c

Then these do satisfy the ring axioms, which is true (but nearly impossible to verify).

In fact, these are the multiplication and addition tables of

where arithmetic is done modulo 2.

Q2) What are polynomials?

A2)

These are some of the most important examples of rings, as mentioned in the previous section.

Definition

Let R be a commutative ring with an identity. Then a polynomial with coefficients in R in an indeterminate x is something of the form

a0 + a1x + a2x2 + ... + anxn where ai ∈ R.

Polynomials are added and multiplied "as usual."

R[x] denotes the ring of such polynomials.

1. Note that each non-zero polynomial has a finite degree: the largest n for which an ≠ 0.
2. The indeterminate x is not a member of R. Neither are x2, x3, ... They are simply "markers" to remind us how to add and multiply.
3. One could (and maybe should) define a polynomial to be a sequence (a0 , a1 , a2 , ... ) in which only finitely many of the terms are non-zero.
4. Two polynomials are equal if and only if they have the same number of coefficients.

Q3) Give properties of Rings?

A3)

A ring in the mathematical sense is a set S together with two binary operators + and * (commonly interpreted as addition and multiplication, respectively) satisfying the following conditions:

1. Additive associativity: For all ,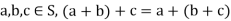

2. Additive commutativity: For all 

3. Additive identity: There exists an element 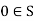 such that for all , ,

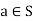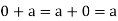4. Additive inverse: For every 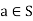 there exists  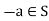such that ,

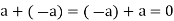5. Left and right distributivity: For all 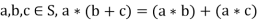 and ,

6. Multiplicative associativity: For all 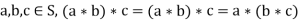 a ring satisfying this property is sometimes explicitly termed an associative ring).

Conditions 1-5 are always required. Though non-associative rings exist, virtually all texts also require condition 6

Rings may also satisfy various optional conditions:

7. Multiplicative commutativity: For all 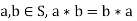  (a ring satisfying this property is termed a commutative ring),

8. Multiplicative identity: There exists an element 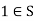 such that for all 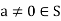,  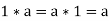(a ring satisfying this property is termed a unit ring, or sometimes a "ring with identity"),

9. Multiplicative inverse: For each  in S, there exists an element 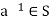 such that for all 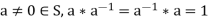, where 1 is the identity element.

A ring that satisfies all additional requirements A field is defined as a set of numbers between 6 and 9, whereas a division algebra is defined as a set of numbers between 6 and 9. (or skew field).

Q4) Define Substring with the help of example.

A4)

These are the ideas in group theory that are equivalent to subgroups and normal subgroups.

A ring's S subring R is a subset of R, which is a ring that may be operated on in the same way as R.

In other words, the condition for a subring.

If a, b S a - b, ab S, then a non-empty subset S of R is a subring.

So, when it comes to subtraction and multiplication, S is closed.

1. A subring of Z is formed by the even numbers 2Z.
2. In general, the set of all multiples of n is a subring nZ of Z if n is any integer.
3. The odd integers do not make up a Z subring.
4. The subsets {0, 2, 4} and {0, 3} are subrings of Z6.
5. The set {a + bi ∈ C | a, b ∈ Z} forms a subring of C.

This is called the ring of Gaussian integers (sometimes written Z[i]) and is important in Number Theory.

6.     The set {a + b√5 | a, b ∈ Z} is a subring of the ring R.

7.     The set {x + y√5 | x, y ∈ Q} is also a subring of R.

8.     The set of real matrices of the form 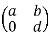  forms a subring of the ring of all 2 × 2 real matrices.

An ideal is a special kind of subring.

Q5) Explain integral domains with the help of examples.

A5)

There are two distinct types of rings.

Definition

If a, b are two ring elements with a, b ≠ 0 but ab = 0 then a and b are called zero-divisors.

Example

In the ring Z6 we have 2.3 = 0 and so 2 and 3 are zero-divisors.
More generally, if n is not prime then Zn contains zero-divisors.

Definition

A commutative ring with an identity (1 0) and no zero-divisors is called an integral domain.

That is ab = 0 ⇒ a = 0 or b = 0.

Examples

1. The ring Z is an integral domain. (This explains the name.)
2. The polynomial rings Z[x] and R[x] are integral domains.
   (Look at the degree of a polynomial to see how to prove this.)
3. The ring {a + b√2 | a, b ∈ Z} is an integral domain.
4. If p is prime, the ring Zp is an integral domain.

Q6) Explain Fields with the help of examples.

A6)

Theorem

Every finite integral domain is a field.

Proof

Only the multiplicative inverse of a typical element a 0 has to be demonstrated.

Consider a, a2, a3, ... Since there are only finitely many elements we must have am = an for some m < n(say).

Then 0 = am - an = am(1 - an-m). Since there are no zero-divisors we must have am ≠ 0 and hence 1 - an-m = 0 and so 1 = a(an-m-1) and we have found a multiplicative inverse for a.

More examples

1. If p is prime Zp is a field. It has p elements.
2. Consider the set of things of the form {a + bx | a, b ∈ Z2} with x an "indeterminate".
   Use arithmetic modulo 2 and multiply using the "rule" x2 = x + 1.
   Then we get a field with 4 elements: {0, 1, x, 1 + x}.
   For example: x(1 + x) = x + x2 = x + (1 + x) = 1 (since we work modulo 2). Thus every non-zero element has a multiplicative inverse.
3. Consider the set of things of the form {a + bx + cx2 | a, b, c ∈ Z2} where we now use the rule x3 = 1 + x.

This gives a field with 8 elements: {0, 1, x, 1 + x, x2, 1 + x2, x + x2, 1 + x + x2}.
For example, (1 + x2)(x + x2) = x + x2 + x3 + x4 = x + x2 + (1 + x) + x(1 + x) = 1 + x since we work modulo 2.

Q7) State the Characteristics of Rings.

A7)

Definition: Let R be a ring. The Characteristic of R denoted char(R) or ch(R) is the smallest nonnegative p such that p⋅1=0. If no such p exists then we define the char(R)=0.

For example, consider the fields Q, R, and C. It is easy to see that the characteristic of each of these fields is 0, for clearly p⋅1=p=0 if equal to 0 if and only if p=0.

For another example, Consider the Galois field, abbreviated as GF (pn). It is simple to establish that this field's characteristic is p.

According to the following theorem, a field's characteristic is always a prime number of 0.

Theorem 1: Let F be a field. Then char(F)=p for some prime p or char(F)=0.

Proof: Suppose that char(F)=n for some n∈N. Then:

Suppose that n is a composite number, say n=rs. Then:

F has no zero divisors because it is a field. As a result, r1=0 or s1=0. However, this contradicts the fact that n is the smallest nonnegative number having this feature. As a result, n=p for some prime p.

Theorem 2: Let F be a field with char(F)=p for some prime p.

Then (a±b)pn=apn±bpn for all a,b∈F and for all n∈N.

Q8) What are Factor rings?

A8)

In Group theory, we follow the evolution of factor groups.

If I is an ideal of a ring R and a ∈ R then a coset of I is a set of the form a + I = {a + s | s I }.

The set of all cosets is denoted by R/I.

Theorem

If I is an ideal of a ring R, the set R/I is a ring under the operations

(a + I) + (b + I) = (a + b) + I and (a + I) . (b + I) = (ab) + I.

Proof

We need to check that the operations are "well-defined". That is if a1 and a2 are representatives of the same coset and b1 and b2 represent the same coset then a1 + b1 and a2 + b2 represent the same coset and so do a1b1 and a2b2.

We have a1 - a2 I and b1 - b2 I and so adding these shows that (a1 + b1) - (a2 + b2) ∈ I and so these do represent the same coset.

Similarly, for the product, observe that a1b1 - a2b2 = (a1 - a2)b1 + a2(b1 - b2) and the result follows from the properties of the ideal.

Once you know that the operations are well-defined the ring axioms follow easily.

Note that the zero of the factor ring is the coset 0 + I or the ideal I itself.

Examples

1. Let I = nZ ⊆ Z.
   Then Z/nZ has n elements: I, 1 + I, 2 + I, ... , (n - 1) + I and the factor ring is Zn.
2. Let I be the ideal of R[x] generated by the polynomial x2 + 1.

Then every coset has a representative of the form (a + bx) + I since if we choose a coset representative (say) x3 then we have x3 = -x + (x2 + 1)x - x + I and so -x will do for a representative instead. You should see that by thinking of x2 + 1 as 0 one can use the "rule" x2 = -1 to get rid of all higher powers.

So we get a ring in which we can add and multiply things like a + bx using the rule x2 = -1 to do multiplication.

If you replace the indeterminate x by i you will see that this is the complex numbers.

That is: R[x]/ < x2+ 1 > C 

1. Using a similar argument we can see that the finite field GF(9) constructed earlier is in fact the factor ring Z3[x]/< x2 + 1 > since the "multiplication rule" x2 = -1 we used is equivalent to x2 + 1 = 0.
2. The ring Z5[x]/< x2 + 1 > has 25 elements since (as above) coset representatives can be chosen to be of the form a + bx with a, b ∈ 5. However, this is not a field since the cosets (x + 3) + I and (x + 2) + I have a product (x + 3)(x + 2) + I = 0 + I. Hence the ring has zero-divisors and is not a field.

Notice that the reason that this happened was that the polynomial x2 + 1 factorises in Z5[x] into a product of factors of lower degree. (You could see it had linear factors since the polynomial has roots in 5.)

The kernel of a ring homomorphism is an ideal, and the image is a subgroup, as we saw in the previous section. It should come as no surprise that we have a matching finding for groups.

Q9) Prove the Isomorphism theorem for Rings?

A9)

If f: R→ S is a ring homomorphism the factor ring R/ker(f) is isomorphic to im(f).

Proof

Define the map θ: R/ker(f)→ im(f) by θ(a + ker(f)) = f(a).

Then the proof is exactly as in the group theory case except you also need to check that this map respects the ring multiplication as well as addition.

The Second Isomorphism Theorem for Rings

Let I and J be ideals of a ring R. Then I + J and I ∩ J are also ideals and the factor rings (I + J)/J and I/(I ∩ J) are isomorphic.

Proof

Here is a picture showing the inclusions. The double lines represent the two factor rings

.

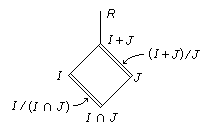
To prove the result, Define θ: I→ (I + J)/J by i ↦ i + J.

Since every coset in (I + J)/J has a representative of this form θ is onto.

If i ∈ ker(θ) then i + J = J and so i ∈ J and hence is in I ⊆ J.

The result now follows from the First Isomorphism Theorem.

The Third Isomorphism Theorem for Rings

Let I and J be ideals of a ring R with I ⊆ J. Then J/I is an ideal of R/I and (R/I)/(J/I)  R/J

Proof

It is easy to verify that J/I is an ideal of R/I.

Define a map θ: R/I→ R/J by a + I ↦ a + J for any coset a + I of I in R. This is clearly onto.

An element a + I is in the kernel of θ if a + I = J which (since I ⊆ J) will only happen if a ∈ J. Thus ker(θ) = J/I ⊆ R/I and the result follows from the the First Isomorphism Theorem.

Q10) State the Operation that can pe performed on Ideals.

A10)

Let R be a ring and let X⊂R. Then recall ⟨X⟩ denotes the ideal generated by X, that is, ∩{J|X⊂J◃R}. Note the empty set generates the zero ideal.

Set L(R)={J|J◃R}. This is a poset with respect to ⊂. Moreover, L(A) is a complete lattice: for any S⊂L(A), we have

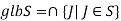
Sums of Sets:

If X,Y⊂R then define X+Y={x+y|x∈X,y∈Y}. Define X+y=X+{y}. This is consistent with our notation for cosets. Also note if J,K◃R then J+K=⟨J∪K⟩.

More generally, if {Ji|i∈I} is a family of ideals in R, then define

Where only finitely many xi are nonzero. Then we have

Finding the least upper bounds in L(R) is thus equal to adding up the sums of families of ideals.

Products of Ideals and Sets:

Now suppose J◃R,X⊂A. Define

We have JX=⟨ax|a∈J,x∈X⟩◃R.

Define Jx=J{x}. Then we have Jx={ax|a∈J}. Note Rx=⟨x⟩, the principal ideal generated by x.

If J,K,L◃R, then (JK)L=J(KL). More generally, if J1,...,Jk◃R then

Powers of Ideals:

Powers of J◃R are defined as follows:

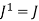
Hence Jk={0} if and only if all products of k elements of J are zero.

Note if J,K◃R then JK⊂J∩K.

Q11) Suppose that I and J are ideals in a ring R. Assume that I ∪ J is an ideal of R. Prove that I ⊆ J or J ⊆ I.

A11)

Assume to the contrary that I is not a subset of J and that J is not a subset of I. It follows that there exists an element i ∈ I such that i 6∈ J. Also, there exists an element j ∈ J such that j 6∈ I. Note that i ∈ I ∪ J and j ∈ I ∪ J. Since we are assuming that I ∪ J is an ideal of R, it follows that i + j ∈ I ∪ J.

Let k = i + j. If k ∈ I, then k − i ∈ I too. That is, j ∈ I. This is not true and hence k 6∈ I. If k ∈ J, then k − j ∈ J too. That is, i ∈ J. However, this is not true and hence k 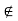J. We have shown that k 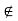I and k J. That is, k 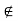I ∪ J. Thus, i + j 6∈ I ∪ J, contradicting what was found in the previous paragraph.

This contradiction prove the stated assertion.

Q12) If R is a ring and a, b, c, d ∈ R, evaluate (a + b)(c + d).

A12)

(a + b)(c + d) = a(c + d) + b(c + d) by distributive law

= (ac + ad) + (bc + bd)

= ac + ad + bc + bd

Q13) D is an integral domain and D is of finite characteristic, prove that the characteristic of D is a prime number.

A13)

Let a be any non zero element of D. Then a 2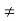 0 as D is an integral domain. Since D is of positive characteristic q, then qa2 = 0 for all a ∈ D.

If q is a composite number, let p1 be a prime number dividing q and let q = p1q1.

Now

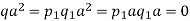
Since D is integral domain either p1a = 0 or q1a = 0. By exercise 3.7, either of these equations gives a contradiction to the assumption that q is the smallest positive integer such that qx = 0 for all x ∈ D. Thus q is not composite, it is a prime.

Q14) Show that the commutative ring D is an integral domain if and only if for a, b, c ∈ D with a 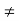0 the relation ab = ac implies that b = c.

A14)

If D is a commutative ring and a 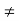0, then ab = ac implies a(b − c) = 0. Since a 6= 0 we obtain b = c

Conversely assume that ab = ac and a 0 implies that b = c. Assume if possible that a 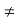0 and ab = 0 Then ab = a0 and hence b = 0

Q15) If D is an integral domain and if na = 0 for some a 6= 0 in D and some integer n 6= 0, prove that D is of finite characteristic.

A15)

Let b ∈ D. Consider nab. Since (na) = 0 we have nab = 0. On the other hand nab = nba as integral domain is a commutative ring. So 0 = nab = nba. But a 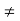0 implies nb = 0 for all b ∈ D.

Q16) If U, V are ideals of R, let U + V = {u + v | u ∈ U, v ∈ V }. Prove that U + V is also an ideal.

A16)

Let u1 + v1 and u2 + v2 be two elements of U + V. Then u1 + v1 − (u2 + v2) = (u1 − u2) + (v1 − v2). Since u1 − u2 ∈ U and v1 − v2 ∈ V, we have (u1 − u2) + (v1 − v2) ∈ U + V. For any r ∈ R we have

r(u + v) = ru + rv ∈ U + V as ru ∈ U and rv ∈ V for any u ∈ U, v ∈ V.

Similarly (u + v)r = ur + vr ∈ U + V as ur ∈ U and vr ∈ V.

Q17) If U is an ideal of R, let r(U) = {x ∈ R | xu = 0 for all u ∈ U}

Prove that r(U) is an ideal of R

A17)

Let x1, x2 ∈ r(U) and let u ∈ U. Then (x1 − x2)u = x1u − x2u = 0 as x1u = 0 and x2u = 0. Hence x1 − x2 ∈ r(U). Now let r ∈ R and x ∈ r(U). Then

(rx)u = r(xu) = 0

(xr)u = x(ru) = 0 as U is an ideal, ru ∈ U.

Hence r(U) is an ideal of R.

Q18) If R is a commutative ring and a ∈ R,

a) Show that aR = {ar | r ∈ R} is a two sided ideal of R

b) Show by an example that this may be false if R is not commutative.

A18)

a) Clearly 0 ∈ aR so aR is non-empty. For any ax, ay ∈ aR

Ax − ay = a(x − y) ∈ aR as x − y ∈ R

Now for any r ∈ R rax = axr as R is commutative. Hence axr ∈ aR. So aR is a two sided ideal of R.

b) Consider the ring R of 2 × 2 matrices over real numbers.

This is not a two sided ideal as

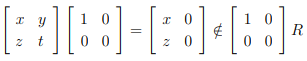
For any z 0

Q19) If A and B are ideals in a ring R such that A ∩ B = (0), prove that for every a ∈ A, b ∈ B, ab = 0.

A19)

Let a ∈ A and b ∈ B. Then

Ab ∈ A as A is an ideal

Ab ∈ B as B is an ideal

Hence ab ∈ A ∩ B = {0}

Q20) Let R be a commutative ring with unit element; prove that every maximal ideal of R is a prime ideal.

A20)

Let R be a commutative ring with unit element and let M be a maximal ideal. Then R/M is a field in particular it is an integral domain. Hence by question 3.44 M is a prime ideal.

Q21) Give an example of a ring in which some prime ideal is not a maximal ideal.

A21)

Let R = Z + Z be the direct sum of the ring of integers. Let I = 0 + Z be an ideal of R. Now R/I is a prime ideal since R/I is isomorphic to Z which is an integral domain. But I is not a maximal ideal since R/I is isomorphic to Z. Since Z is not a field we obtain I is not a maximal ideal.

An integral domain R is said to be a Euclidean ring if for every a 6= 0 in R there is defined a non-negative integer d(a) such that

(1) For all a, b ∈ R both non-zero, d(a) ≤ d(ab).

(2) For any a, b ∈ R both non-zero, there exists t, r ∈ R such that a = tb + r where either r = 0 or d(r) < d(b).

Q22) If R is a ring, let Z(R) = {x ∈ R | xy = yx all y ∈ R}. Prove that Z(R) is a subring of R.

A22)

Clearly 0 ∈ Z(R), so Z(R) 6= ∅. Let x, y ∈ Z(R) and let r ∈ R.

(x − y)r = xr − yr. Since x and y are in the center this is equal to rx − ry = r(x − y). So x − y ∈ Z(R). Now (xy)r = x(yr) = x(ry) = (xr)y = r(xy) for all r ∈ R.

Hence xy ∈ Z(R).