Unit - 3

Polynomial rings over commutative rings

Q1) Show that f(x) = x3 −3x + 3 is irreducible in Q[x]. (b) Show that f(x) = x3 −3x + 3 is reducible in F5[x]

A1)

Suppose f is reducible. If f = is a nontrivial factorization of f, then deg(g)+deg(h) = 3, so either g has degree 1 and h has degree 2 or vice versa (since g and h are not constants). So f has a factor of the form (ax+b) where a,b∈Q and a ̸=0. It follows that −b/a is a root of f, so f has a root in Q. Write the root of f in the form m/n where m,n∈Z with gcd(m,n) = 1. Then f(m/n) = 0 implies m3 −3mn2 + n3 = 0. So n divides 3mn2−n3 = m3 but gcd(m,n) = 1, so n = 1. It follows that f has an integer root. Now since f ∈Z[x], we can reduce coefficients modulo 2 and obtain a polynomial f mod 2 ∈F2[x]. Note that f mod 2 does not have a solution in F2, since f(0) ≡1 mod 2 and f(1) ≡1 mod 2. It follows that f does not have an integer root, which is a contradiction. So f is irreducible in Q[x]. On the other hand, note that f(2) ≡0 mod 5. So 2 is a solution of fin F5. Divide f by (x −2) in F5[x], to find the factorization f(x) ≡(x + 1)2(x −2) mod 5.

Q2) State and prove The Euclidean algorithm?

A2)

If d is the gcd of a, b there are integers x, y such that d = ax + by.

Proof

Here is an example: Take a = 76, b = 32:

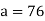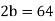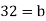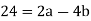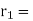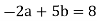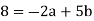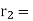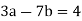In general, use the procedure: divide (say) a by b to get remainder r1. Note that one can write r1 in terms of a and b.

Then divide b by r1 to get remainder r2. Note that one can write r2 in terms of b and r1 and hence in terms of a and b.

Repeat the process getting smaller and smaller remainders r1 , r2 , ... Which must eventually lead to a remainder of 0.

Ri may be stated in terms of a and b at each stage since the latest non-zero remainder d divides all the previous ones, and hence both a and b. As a result, it divides gcd (a, b). Because d may be expressed in terms of a and b, gcd(a, b) divides d and must be d.

Q3) Prove:   If a(x), b(x) ∈ R[x] with b(x) ≠ 0 then ∃ q(x), r(x) ∈ R[x] such that a(x) = b(x)q(x) + r(x) with either r(x) = 0 or deg(r(x)) < deg(b(x)).

A3)

We use the (slightly less well-known) process of dividing one polynomial by another (of lower degree). It is just like long division.

Take a(x) = 3x4 + 2x3 + x2 - 4x + 1 and b = x2 + x + 1

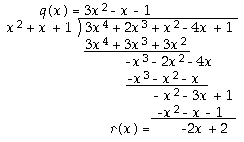
Q4) Solve the following examples?

1. Factor

2. Factor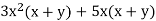

3. Factor

A4)

1. Factor

Since is a common factor, we have

Multiplying as in the previous chapter, we find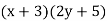

2. Factor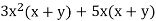

We see that x and x+y are common factors.

3. Factor

Q5) Solve: Factor

A5)

To begin, keep in mind that not all four terms in the statement share a common component, but some do. For example, the first two terms can be factored to provide 3(ax + 2y). We get a(ax + 2y) by factoring a from the remaining two terms. The expression is now 3(ax + 2y) + a(ax + 2y), and we can factor as (axe + 2y)(3 + a) because we have a common factor of (axe + 2y). We get the original expression 3ax + 6y + a2x + 2ay by multiplying (axe + 2y)(3 + a) and observe that the factoring is valid.

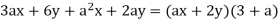
The first two terms

The remaining two terms

is now a factoring problem

Because we "grouped" the terms two at a time, this is an example of factoring by grouping.

Q6) Prove this: If f(T) ∈Z[T] is monic and there is a prime p such that f(T) is irreducible in (Z/pZ)[T] then f(T) is irreducible in Q[T].

A6)

Proof. By Gauss’ lemma, to prove f(T) is irreducible in Q[T] it suffices to show we can’t write f(T) as a product of lower-degree factors in Z[T].

Assume f = gh for some g,h∈Z[T] with degg<degf and degh<degf. We will get a      contradiction from this.

Looking at the leading coefficients on both sides of f = ghwe have 1 = (lead g)(lead h) in Z, so g and h both have leading coefficient 1 or both have leading coefficient −1. Therefore, after changing the signs on g and h if necessary, we can assume g and h are both monic in Z[T]. Reduction mod p is a ring homomorphism Z[T] →(Z/pZ)[T], so it turns the equation f = ghin Z[T] into f = ghin (Z/pZ)[T]. Since f is irreducible, one of g or h has degree 0 and the other has degree equal to that of f. Because f, g and h are all monic,

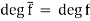
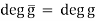
Therefore one of g or h has degree equal to the degree of f, but this contradicts g and h both having degree less than degf.             

Q7) Explain the Eisenstein's Irreducibility Criterion?

A7)

The irreducibility criterion of Eisenstein is a way for proving irreducibility of a polynomial with integer coefficients (that is, cannot be written as a product of two polynomials of smaller degree with integer coefficients). It is not generally relevant to most polynomials due to its unique requirements, but it is useful for displaying examples of properly chosen irreducible polynomials.

Let ​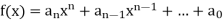 be a polynomial with integer coefficients. Suppose that there exists a prime pp, such that

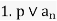
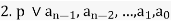
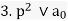
Then f(x) is irreducible over the integers.

Q8) Explain and prove the Extended Eisenstein's Criterion?

A8)

Let 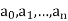 be integers. Then, Eisenstein's Criterion states that the polynomial  has an irreducible factor of degree more than 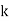 if:

1)  is a prime which divides each of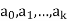 

2) 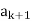 is not divisible by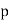 

3) 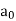 is not divisible by 

Proof

Let

,

Where 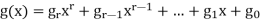 and 

.

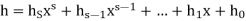Since  has only one factor of p, we know that or 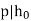. WLOG, assume 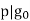. Then, we know that . This means 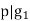. Similarily, we see, if  for all 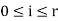. This means that 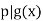, so 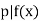. However, we know that  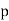does not divide by a contradiction. Therefore, .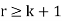

Q8) Prove this “Let F be a field. Then the polynomial ring F[x] is a UFD”

A9)

We need to show that every non-zero non-unit in F[x] can be written as a product of irreducible polynomials in a manner that is unique up to order and associates.

So let f(x) be a polynomial of degree n ≥ 1 in F[x]. If f(x) is irreducible there is nothing to do. If not then f(x) = g(x)h(x) where g(x) and h(x) both have degree less than n. If g(x) or h(x) is reducible further factorization is possible; the process ends after at most n steps with an expression for f(x) as a product of irreducibles. To see the uniqueness, suppose that

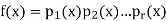and

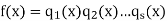
Are two such expressions, with s ≥ r. Then q1(x)q2(x)...qs(x) belongs to the ideal hp1(x)iof F[x]. Since this ideal is prime (as p1(x) is irreducible) this means that either q1(x) ∈hp1(x)ior q2(x)...qs(x) ∈hp1(x)i. Repeating this step leads to the conclusion that at least one of the qi(x) belongs to hp1(x)i. After reordering the qi(x) if necessary we have q1(x) ∈hp1(x)i. Since q1(x) is irreducible this means q1(x) = u1p1(x) for some unit u1. Then

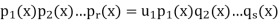
Since F[x] is an integral domain we can cancel p1(x) from both sides to obtain

After repeating this step a further r −1 times we have

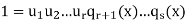
Whereu1,...,ur are units in F[x] (i.e. non-zero elements of F). This means s = r, since the polynomial on the right in the above expression must have degree zero. We conclude that q1(x),...,qs(x) are associates (in some order) of p1(x),...,pr(x). This completes the proof.             

Unique Factorization in [X] Every polynomial in [X] that is not the zero polynomial or a unit in [X] can be written in the form cp1(X)p2(X) ····· pm(X), where c is a constant and the pi(X) ′ s are irreducible polynomials of positive degree. Furthermore, if

Then c = ±d, n = m, and after renumbering the q(x) ′ s, pi(x) = ±qi(x), for i = 1, 2, . . . , m.

Q9) Solve

a) Factor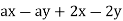

b) Factor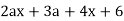

A10)

a) Factor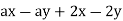

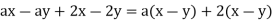
b) Factor

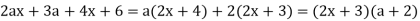
Q10) Factor 12x3 + 6x2 + 18x.

A11)

It should not be required to list the elements of each phrase at this point. You should be able to figure out the most common component in your head. Individualizing the pieces is a smart practise to follow. To put it another way, don't try to acquire all of the common components at once; instead, get the number first, then each letter involved. 6 is a factor of 12, 6, and 18, for example, and x is a factor of each phrase. As a result, 6x(2x2 + x + 3) = 12x3 + 6x2 + 18x. We can see that the terms within the parenthesis have no other common factor when we multiply, therefore we know the solution is accurate.

Q11) Factor 3ax + 2y + 3ay + 2x.

A12)

The first two terms have no common element, but the first and third terms have, so the third term will be placed after the first. Always keep an eye on the future to see how the terms might be arranged.

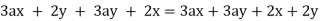
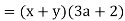
It is critical to ensure that the factors within parenthesis are identical in all circumstances. This may need the use of a negative number or letter as a factor.

Remember, the commutative property allows us to rearrange these terms.
Multiply as a check.

Q12) Factor ax - ay - 2x + 2y.

A13)

It's worth noting that if we subtract a from the first two terms, we get a. (x - y). When we factor +2 into the last two numbers, we get 2(-x + y), but when we factor "-2," we get - 2 (x - y). We proceed in this manner because we want the terms within parenthesis to be (x - y).

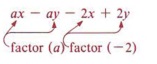
Q13) Factor

A14)

Because this is a trinomial with no common factor, we'll factor it using the multiplication pattern.

First write parentheses under the problem.

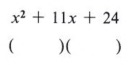
We now wish to fill in the terms so that the pattern will give the original trinomial when we multiply. The first term is easy since we know that (x)(x) = x2.

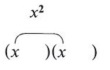
Remember, the product of the first two terms of the binomials gives the first term of the trinomial.

Now we must discover integers that multiply to provide 24 while also adding to get the middle term. It's worth noting that the first and last terms in each of the following examples are correct.

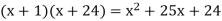
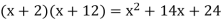
Only the last product has a middle term of 11x, and the correct solution is

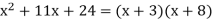
This method of factoring is called trial and error - for obvious reasons.

Some number facts from arithmetic might be helpful here.

1. The product of two odd numbers is odd.
2. The product of two even numbers is even.
3. The product of an odd and an even number is even.
4. The sum of two odd numbers is even.
5. The sum of two even numbers is even.
6. The sum of an odd and even number is odd.

Therefore, when we factor an expression such as x2 + 11x + 24, we know that the product of the last two terms in the binomials must be 24, which is even, and their sum must be 11, which is odd.

Thus, only an odd and an even number will work. We need not even try combinations like 6 and 4 or 2 and 12, and so on.

Q14) Show that the set of Gaussian integers [i] = {a + ib: a, b ∈ Z} where i = √ −1, equipped with the usual addition and multiplication of complex numbers, is a ring.

A15)

Since [i] is a subset of the complex numbers C, it will be enough to prove that [i] is a subring of C. We check the conditions of Lemma 1.8. Consider two elements a + ib and c + id of [i]. Then

SR1: (a + ib) − (c + id) = (a − c) + i(b − d) ∈ [i].

SR2: (a + ib) · (c + id) = (ac − bd) + i(ad + bc) ∈ [i].

SR3: The multiplicative identity of C and [i] is 1 = 1 + 0i.

It follows from the subring criterion that 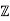[i] is a subring of C, and therefore that 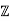[i] is a ring.

Q15) Condition SR3 does not hold for S: the multiplicative identity of Z10 is 1, which is not in S.

A16)

Note, however, that S is a ring with the same operations as Z10. The multiplicative identity of S is 5.

Q16) Let f(x) = 1 + 2x and g(x) = 1 + 3x + 2x 3 be polynomials in 5[x], the ring of polynomials over the field 5, equipped with addition and multiplication modulo 5. (a) Calculate and simplify (i) f(x) + g(x), and (ii) 3f(x) − g(x). (b) Compute f(x)g(x).

(a) Calculate and simplify (i) f(x) + g(x), and (ii) 3f(x) − g(x).

(b) Compute f(x)g(x).

A17)

(a) (i) f(x) + g(x) = (1 + 1) + (2 + 3)x + 2x 3 ≡ 2 + 2x 3 (mod 5)

(ii) 3f(x) − g(x) = 3(1 + 2x) − (1 + 3x + 2x 3

= (3 + (3 × 2)x) − 1 − 3x − 2x 3

= (3 + 4) + (1 + 2)x + 3x 3

≡ 2 + 3x + 3x 3 (mod 5)

(b) f(x)g(x) = (1 + 2x)(1 + 3x + 2x 3

= 1 + 5x + 6x 2 + 2x 3 + 4x 4

≡ 1 + x 2 + 2x 3 + 4x 4 (mod 5)

Q17) Let p be a prime and suppose that f(x)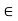Z[x] with deg f(x)≥1. Let f′(x) be the polynomial in Zp[x] obtained from f(x) by reducing all the coefficients of f(x) modulo p. If f′(x) is irreducible over Zp and deg f(x)= deg f′(x), then f(x) is irreducible over Q. Prove.

A18)

The proof goes by contradiction, by assuming there exists a reducible f(x)∈Z[x] such that deg f′(x)=deg f(x) and f′(x) is irreducible in Z p[x]. The proof shows that then necessarily f′(x) is reducible in Z p[x], because f′(x)=g′(x)h′(x), a contradiction.

Note that if deg f′(x)=deg f(x) and f(x)=g(x)h(x),  

Then deg g′(x)=deg g(x) and deg h′(x)=deg h(x).

So g′(x) and h′(x) are not units in Z p[x] because g(x) and h(x) are not units in Z[x].