Unit - 1

Metric spaces

Q1) Define metric space.

A1)

Suppose there is

a non-empty set X. A function 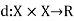is said to be a metric space if d satisfies the conditions given below-

1. for all 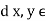X and d(x, y) = 0 if an only if x = y.
2. d(x , y) = d(y , x) for all x , y E X.
3. d(x, z) < d(x, y) + d(y, z) for all x, y, z E X. This is called the triangle inequality.

For x, y E X, d(x, y) is called the distance between x and y.

The pair (X, d) is then called a metric space.

Q2) Give some properties of metric space.

A2)

1. The distance between x and y is non-negative and it is equal to zero when and only when x and y coincide,
2. The distance between x and y is the same as the distance between y and x. This is the property of symmetry.
3. The distance between x and y is not more than the distances between x and z and that between z and y, added together. This is called the triangle inequality.

Q3) Consider the function 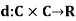such that .

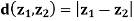Here we know that the absolute function on C follows the properties given below-

1. |z| 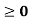and |z|=O if and only if z = 0
2. |-z| = |z|

A3)

Hence it is very easy to verify that d satisfies conditions (I) and (2) in Definition of metric space.

To show the triangular inequality 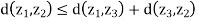we use the inequality

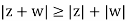with z = 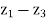, w = 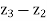, we can verify this inequality.

This shows that d is a metric.

Q4) Define a sequence in metric space.

A4)

A sequence assigns to each n 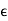N a uniquely determined element

Of X. If f (n) = 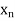, it is customary to denote the sequence by the symbol 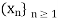or

or by x1, x2, . . . , xn, . . . .

Q5) What is Cauchy’s sequence?

A5)

Let d be a metric on a set X. A sequence 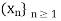in the set X is said to be a Cauchy sequence if, for every 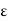> 0, there exists a natural number n0 such that

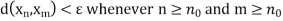
Q6) In C[0,1], the sequence f1, f2, f3, . . . Given by

Is Cauchy in the uniform metric. For m n the function

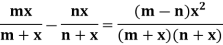
A6)

Being continuous on [0, 1], assumes its maximum at some point x0 [0,1]. So,

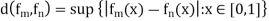
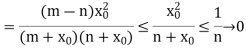
For large m and n. Moreover, the sequence converges to some limit. For f(x) = x

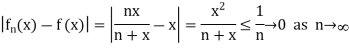
Therefore,   converges to the limit f, where f (x) = x for all x [0, 1].

Q7) Define complete metric space.

A7)

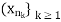Let be a given sequence in a metric space (X,d) and let be a sequence of positive integers such that   Then the sequence  is called a subsequence o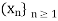f . If 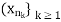converges, its limit is called a sub-sequential limit of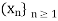

It is clear that a sequence 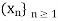 in X converges to x if and only if every subsequence of it converges to x.

Q8) The metric space X = 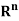with the metric given by

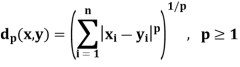
Where x = (x1, x2, . . . , xn) and y = (y1, y2, . . . , yn) are in 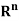, is a complete metric space.

A8)

Let 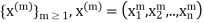denote a Cauchy sequence in

(X,d), I.e. 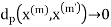as Then, for a given there exists

An integer 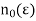such that

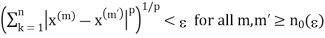………………(1)

For all 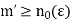letting 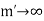in equation (2), we have-

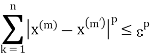
For all 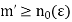which means 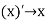in (X, d).

Q9) Define isometric.

A9)

Let (X, d) and (X’,d’) be two metric space. A mapping f of X into X’ is an isometry if

d’(f(x), f(y)) = d(x, y)

For all x, y 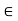X. The mapping f is also called an isometric embedding of X into X’. If, however, the mapping is onto, the spaces X and X’ themselves, between which there exists an isometric mapping, are said to be isometric. It may be noted that an isometry is always one-to-one.

Q10) Explain open and closed balls.

A110)

Let (X, d) be a metric space. The set

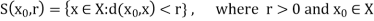
Is called the open ball of radius r and centre x0. The set

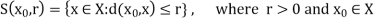
Is called the closed ball of radius r and centre x0.

Q11) In any metric space (X, d), each open ball is an open set. Prove.

A11)

First observe that S(x,r) is nonempty, since x 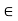S(x, r). Let y 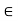S(x, r), so that d(y, x) < r, and let r’ = r – d(y, x) > 0. We shall show that S(y, r’) 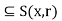as illustrated in figure. Consider any x 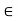S(x, r’), Then we have

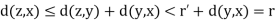
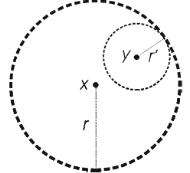
Which means z S(x, r). Thus, for each y S(x, r), there is an open ball S(y, r’) Therefore S(x, r) is an open subset of X.

Q12) A subset G in a metric space (X, d) is open if and only if it is the union of all open balls contained in G. Prove.

A12)

Suppose that G is open. If G is empty, then there are no open balls contained in it. Thus, the union of all open balls contained in G is a union of an empty class, which is empty and therefore equal to G. If G is nonempty, then since G is open, each of its points is the centre of an open ball contained entirely in G. So, G is the union of all open balls contained in it.

Q13) Let A be a subset of a metric space (X, d). Then

(i) 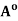is an open subset of A that contains every open subset of A;

(ii) A is open if and only if A =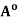

Prove.

A13)

Let x  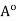 be arbitrary. Then, by definition, there exists an open ball S(x, r) 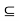A. But S(x,r) being an open set, each point of it is the centre of some open ball contained in S(x,r) and consequently also contained in A. Therefore each point of S(x,r) is an interior point of A, i.e., S(x, r)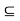 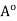Thus, x is the centre of an open ball contained in 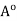Since x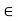   is arbitrary, it follows that each x 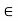has the property of being the centre of an open ball contained in 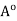Hence, 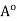is open.

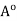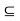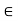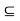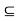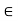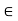
It remains to show that contains every open subset G A. Let x G. Since G is open, there exists an open ball S(x, r) G A. So x 2 A This shows that x G x In other words, G 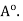(ii) is immediate from (i).

Q14) Explain Cantor’s theorem.

A14)

First, we need to show that 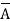< 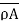: define an injection f:A→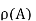by f(a)={a}. Now we need to show that there is no bijection g:A→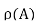. For a contradiction, suppose gg is such a bijection. Let

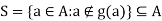
Since S ∈ 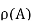, S = g(x), for some x ∈ A, because g is a surjection. There are two possibilities: x ∈S and x ∉ S

If x ∈ S, then x ∉ g(x)=S, i.e., x ∉ S, a contradiction.

2. If x ∉ S, then x ∈ g(x) = S, i.e., x ∈ S, a contradiction.

Therefore, no such bijection is possible

Cantor's theorem implies that there are infinitely many infinite cardinal numbers, and that there is no largest cardinal number. It also has the following interesting consequence:

It also has the following interesting consequence:

There is no such thing as the "set of all sets''.