Unit - 3

Continuity

Q1) What do you understand by continuous metric space.

A1)

Let (X, 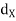) and (Y, 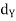) be metric spaces and A 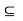X. A function

f : A 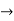Y is said to be continuous at a 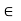A, if for every 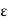> 0, there exists some

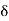> 0 such that

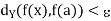whenever and

If f is continuous at every point of A, then it is said to be continuous on A.

Q2) Define extension and restriction.

A2)

Let X and Y be abstract sets and let A be a proper subset of X. If f is a mapping of A into Y, then a mapping g : X 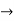Y is called an extension of f if g(x) = f (x) for each x 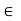A; the function f is then called the restriction of g to A.

Q3) Composite of continuous functions is continuous: Let X ,Y, Z be metric spaces. Let f: X 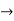Y be continuous at x 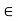X and g: Y 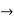Z be continuous at y = f (x). Then the composite map gof: X 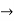Z is continuous at x 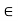X. Prove.

A3)

Let 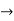x. Then 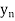:= f ( ) 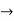y = f (x) by the continuity of f at

x. Since g is continuous at y, it follows that g(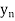 ) ---* g(y) or what is the

Same, g ( f (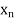 )) 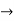g(f (x)).

Q4) Define uniform continuity.

A4)

Let (X,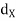) and (Y, 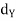) be two metric spaces. A function f : X 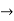Y is said to be uniformly continuous on X if, for every 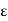> 0, there exists a 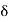> 0 (depending on 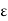alone) such that

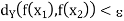whenever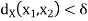

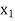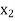
For all , X.

Every function f : X 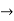Y which is uniformly continuous on X is necessarily continuous on X. However, the converse may not be true.

Q5)  Let (X, d) be a metric space and let x 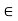X and A X be nonempty. Then x 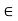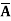if and only if d(x, A) = 0. Prove.

A5)

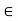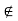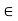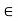
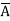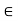Suppose d(x, A) = 0. There are two possibilities: x A or x A. If x A, then x . We shall next show that if x A, then x is a limit point of A. Let e > 0 be given. By the definition of d(x, A), there exists a y A such that d(x, y) < 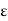, i.e., y S(x, 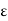). Thus, every ball with centre x and radius e contains a point of A distinct from x; so x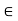 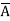. Conversely, suppose x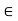 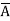.. If x A, then obviously d(x, A) = 0. We shall next show that if x is a limit point of A, then d(x, A) = 0. By the definition of limit point, every ball S(x, 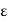) with centre x and radius > 0 contains a point y 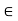A distinct from x.

Consequently, d(x, A) < 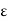, i.e., d(x, A) = 0.

Q6) If f and g are two uniformly continuous mappings of metric spaces (X, 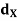) to (Y, 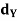), and (Y, 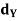) to (Z, 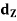), respectively, then g O f is a uniformly continuous mapping of (X, 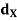) to (Z, 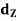). Prove.

A6)

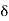Since g is uniformly continuous, for each > 0, there exists a > 0 such that

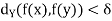implies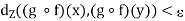

For all x, y 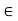  X.

Thus, for each 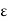> 0, there exists an 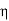> 0 such that

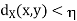implies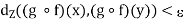

For all x, y 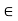X  and so g o f is uniformly continuous on X.

Q7) Let (X, d) be a metric space and let x 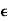X and A 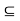X be nonempty. Then x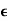   if and only if d(x, A) = 0. Prove.

A7)

Suppose d(x, A) = 0. There are two possibilities: x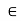  A or x 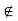A. If x 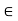A, then x  . We shall next show that if x A, then x is a limit point of A. Let e > 0 be given. By the definition of d(x, A), there exists a y 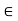A such that d(x, y) < e, i.e., y S(x, e). Thus, every ball with centre x and radius e contains a point of A distinct from x; so x 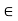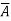. Conversely, suppose x 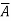. If x 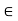A, then obviously d(x, A) = 0.

We shall next show that if x is a limit point of A, then d(x, A) = 0. By the definition of limit point, every ball S(x, e) with centre x and radius e > 0 contains a point y A distinct from x. Consequently, d(x, A) < e, i.e., d(x, A) = 0.

Q8) Explain homomorphism.

A8)

Let (X, 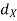) and (Y, 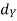) be any two metric spaces. A function f : X 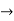Y which is both one-to-one and onto is said to be a homeomorphism if and only if the mappings f and inverse of f are continuous on X and Y, respectively. Two metric spaces X and Y are said to be homeomorphic if and only if there exists a homeomorphism of X onto Y, and in this case, Y is called a homeomorphic image of X.

Q9) Define equivalent metric space.

A9)

A sequence converges to x in (X, d1) if and only if it converges to x in (X, d2).We then say that d1 and d2 are equivalent metrics on X and that (X, d1) and (X, d2) are equivalent metric spaces.

Q10) Define isometry.

A10)

Let (X,d) and (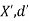) be two metric spaces. A mapping f of X into 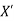is an isometry if

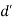(f (x), f (y)) = d(x, y)

For all x, y 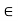X. The mapping f is also called an isometric embedding of X into

If, however, the mapping is onto, the spaces X and 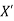themselves, between which there exists an isometric mapping, are said to be isometric. It may be noted that an isometry is always one-to-one.

Q11) A mapping f : X Y is continuous on X if and only if 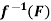is closed in X for all closed subsets F of Y. Prove.

A11)

Let F be a closed subset of Y. Then Y\F is open in Y so that f

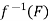is open

In X.

[Note-A mapping f : X 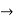Y is continuous on X if and only if  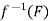is open in X for all open subsets G of Y.]

But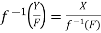

Is open in X. Since every open subset of Y is a set of the type Y\F, where F is a suitable closed set, it follows by using (note) that f is continuous.

The characterisation of continuity in terms of open sets leads to an elegant and brief proof of the fact that a composition of continuous maps is continuous.

Q12) Let (X, 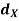) and (Y, 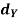) be a metric space and let f:X, g : X Y  be continuous maps. Then the set 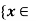X:f(x) = g(x)} is a closed subset of X. Prove.

A12)

Let F = 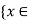X:f(x) = g(x)}. Then X\F =X:f(x) 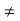g(x)}. We shall

Show that X\F is open. If X\F = 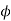, then there is nothing to prove. So let X\F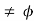  

And let a 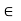X\F. Then f (a)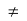g(a). Let r > 0 be the distance dY (f (a), g(a)). For

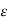= r/3, there exists a 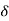> 0 such that

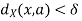implies 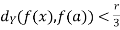and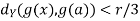

By the triangle inequality, we have

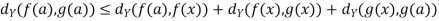
Implies

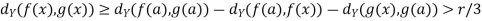
For all x satisfying 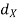(x, a) < 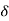. Thus, for each x 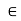 S(a, 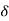), 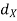(f (x), g(x)) > 0, i.e.,

f (x) 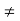g(x). So,

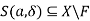
Hence, X\F is open and thus F is closed.

Q13) Let (X, d) be a metric space and let x 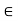X and A 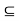X be nonempty. Then x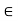 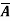if and only if d(x, A) = 0. Prove.

A13)

Suppose d(x, A) = 0. There are two possibilities: x 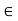A or x 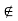A. If x 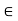A,

Then x 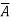. We shall next show that if x 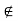A, then x is a limit point of A. Let e > 0

Be given. By the definition of d(x, A), there exists a y 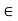A such that d(x, y) < 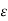, i.e., y S(x, ). Thus, every ball with centre x and radius e contains a point of A distinct from x; so x 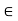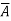. Conversely, suppose x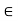 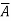.. If x A, then obviously d(x, A) = 0. We shall next show that if x is a limit point of A, then d(x, A) = 0. By the definition of limit point, every ball S(x, 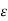) with centre x and radius 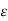> 0 contains a point y 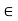A distinct from x.

Consequently, d(x, A) < , i.e., d(x, A) = 0.

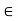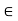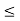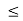Q14) Let A and B be disjoint closed subsets of a metric space (X, d). Then there is a continuous real-valued function f on X such that f (x) = 0 for all x A, f (x) = 1 for all x B and 0f (x)1 for all x 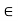X. Prove.

A14)

The mappings x 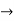d(x, A) and

x d(x, B) are continuous on X. Since A and B are closed and A 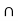B = ,

d(x, A) + d(x, B) > 0 for all x 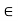X. Indeed, if d(x, A) þ d(x, B) = 0 for some x 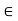X, then d(x, A) = d(x, B) = 0; so x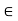 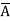= A and x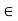 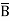= B, and hence x 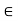A 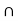B, a contradiction

Now define a mapping f : X  R by

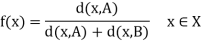
Then f is continuous on X. Moreover,

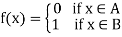
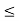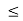And 0f (x)1: