Unit - 4

Contraction mappings

Q1) Define contraction mapping.

A1)

Let (X, d) be a metric space. A mapping Tof X into itself is said to

Be a contraction (or contraction mapping) if there exists a real number

a, 0 < a < 1, such that

d(Tx, Ty)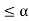d(x, y)

For all x, y 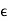X.

Note- a contraction mapping is uniformly continuous

A point x 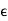  X is called a fixed point of the mapping T : X 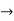X if Tx = x.

Q2) Suppose 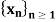is a sequence in any metric space (X, d) and k a positive integer such that each of the k subsequences

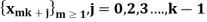
Converges to the same limit x. Then 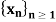converges to x. Prove.

A2)

Given 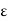> 0, there exist positive integers 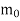, 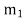. . . , such that

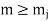implies

Take  N = max {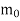, 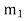. . . ,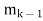}. Consider any n Nk. By the division algorithm,

N = mk + j, where 0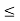j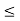k - 1. Since mN -1 would imply that

N 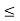  (N - 1)k+ j 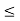(N - 1)k+ (k- 1) = Nk - 1, we must have m>N - 1, so that

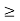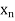mN for j = 0, 1, 2, . . . ,k- 1. It follows that d( ,x)<, i.e., d(,x)<.

This has been proved for any nNk. Therefore, converges to x.

Q3) Give definition of Picard’s existence theorem.

A3)

Consider the domain D: = {(x,y) 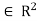 : |x-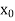 | < a, |y- 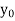| < b } . Assume that

f: D 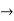R is a continuous function satisfying the Lipschitz condition in the y-variable uniformly in the x-variable, that is,

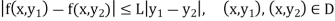
Then there exists a 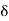> 0 and g:[ 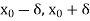] 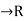  which is a solution of the initial value problem-

g’(x) = f (x, g(x)) satisfying the initial condition g() =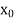

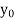
Q4) Define connectedness.

A4)

A (metric) space X is said to be connected if the only sets which are both open and closed in X are and the full space X, when X is a metric space.

A subset A of a metric space X is said to be connected if A is a connected space when considered as a (metric) space with the induced (or subspace) topology. More explicitly, this amounts to saying that (A, 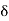) is connected, where .5 is the restriction of the metric d on X to A.

Q5) Let (X, 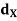) be a connected metric space and f : (X, ) 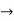(Y, 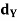) be a continuous mapping. Then the space f (X) with the metric induced from Y is connected. Prove.

A5)

The map f : X 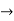f (X) is continuous. If f (X) were not connected, then there would be,  a continuous mapping, g say, of f (X) onto the discrete two element space (, 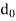). Then g o f :X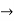 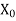would also be a continuous mapping of X onto 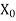, contradicting the connectedness of X.

Q6) Let I = [_ 1, 1] and let f : I 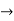  I be continuous. Then there exists a point c  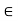I such that f (c) = c. Prove.

A6)

If f (- 1) = -1 or f (1) = 1, the required conclusion follows; hence, we can assume that f (-1) > -1 and f (1) < 1. Define

g(x) = f (x) - x, x 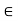 I :

Note that g is continuous, being the difference of continuous functions, and that it satisfies the inequalities g(-1) = f (-1) + 1 > 0 and g(1) = f (1) - 1 < 0. Hence, by the Weierstrass intermediate value theorem, there exists c 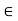(- 1, 1) such that g(c) = 0, that is, f (c) = c.

Q7) If Y is a connected set in a metric space (X, d) then any set Z such that Y 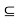Z 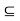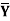is connected. Prove.

A7)

Suppose A and B are two nonempty open sets in Z such that A 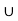B = Z and A 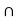B = 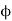1; as Y is dense in Z, Y 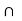A and Y 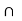B are nonempty open sets in Y and we have

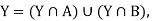
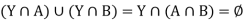
a contradiction.

Q8) Define local connectedness.

A8)

A metric space (X, d) is said to be locally connected if, for x 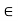X, there is a base of connected neighbourhoods of x. Thus, X is locally connected if and only if the family of all open connected sets is a base for the open subsets of X

Q9) Let (X, d) be a metric space. X is locally connected if and only if the connected components of the open sets in X are open in X. (For any subset A of X, the connected components of the points of the subspace A are called the connected components of A). Prove.

A9)

Let G be an open subset of X, and C be a component of G, and {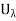:  L} be a basis consisting of open connected sets for the open sets of X.

Let x 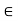C. Since x 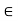G, there is a 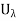such that x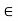   G; but since C is the component of x and 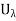is connected, x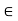 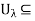C.We have thus shown that C is a union of open subsets of X and is, therefore, open.

On the other hand, if O is any open set containing a point x X, the connected component of x in the subspace O is a connected neighbourhood of x contained in O; hence, X is locally connected.

Q10) What is path-wise connectedness.

A10)

Let (X, d) be a metric space, Y 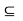X and I = [0, 1]. A path in Y is a continuous mapping f : I Y . If f : I 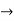Y is a path in Y, we call f (0) 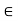Y its initial point, f (1) 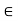Y its final point and say that f joins f (0) and f (1) or that f runs from f (0) to f (1). A subset Y of X is said to be path-wise connected if, for any two points in Y, there exists a path running from one to the other, i.e. the points can be ‘‘joined by’’ a path in Y.

Q11) A totally bounded metric space is bounded. Prove.

A11)

Let (X, d) be totally bounded and suppose 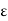> 0 has been given. Then there exists a finite 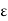-net for X, say A. Since A is a finite set of points, d(A) =  sup{d(y, z): y, z 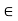A} < 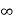. Now, let x1 and x2 be any two points of X. There exist points y and z in A such tha

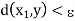and

It follows, using the triangle inequality, that

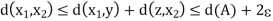
So that

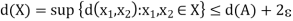
And, hence, X is bounded.

Q12) Let (X, d) be a compact metric space. Then (X, d) is totally bounded. Prove.

A12)

For any given > 0, the collection of all balls S(x, 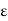) for x X is an open cover of X. The compactness of X implies that this open cover contains a finite subcover. Hence, for 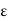> 0, X is covered by a finite number of open balls of radius 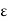, i.e., the centres of the balls in the finite subcover form a finite 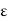-net for X. So, X is totally bounded.

Q13) Any continuous function from a compact metric space to any other metric space is uniformly continuous. Prove.

A13)

Let f: (X, d) 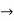(Y, d) be continuous. Assume that X is compact.

We need to prove that f is uniformly continuous on X.

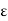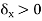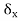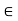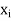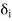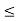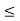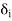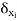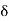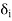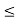A naive attempt would runs as follows. For a given > 0, for each x, there exists by continuity of f at x. Since X is compact, the open cover {B(x, ): x X} admits a finite subcover, say, {B( , ) : 1 j n} where = . One may be tempted to believe that if we set = min{ : 1 i 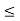n, it might work. See where the problem is. Once you arrive at a complete proof, you may refer to the proof below. We now modify the argument and complete the proof. Given 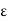> 0, by the continuity of f at x, there exists an 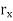> 0 such that

Instead of the open cover {B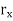(x, ) : x X}, we consider the open

Cover {B(x, 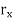/2) : X 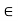X and apply compactness. Let {B(x„ 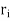/2) : 1 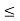i 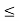n} be a finite subcover. (Here 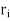= 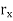„ 1 j 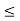n.) Let

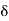:= min{ 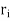/2 : 1 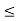j 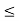n}. Let x, y X be such that d(x, y) < 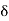. Now

B (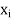, 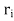/2) for some i. Since d(x, y) < 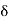, we see that

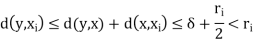
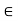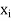Thus y B (,). It follows that

By our choice of 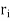. Thus f is uniformly continuous.

Q14) Define totally bounded metric space.

A14)

The metric space (X, d) is said to be totally bounded if, for any 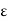> 0, there exists a finite 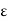-net for (X, d). A nonempty subset Y of X is said to be totally bounded if the subspace Y is totally bounded.