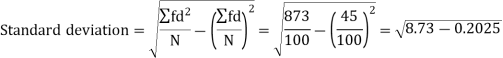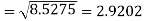Unit - 2
Mathematical Expectation
Q1) What is expectation of a random variable?
A1)
The behaviour of a random variable. (either discrete or continuous) is completely characterized by the distribution function F (x) or density f (x) [P (xi ) in discrete case]. Instead of a function, a more compact description can be made by a single numbers such as mean (expectation), median and mode known as measures of central tendency of the random variable X.
Definition:
Let a random variable X has a probability distribution which assumes the values say with their associated probabilities
with their associated probabilities  then the mathematical expectation can be defined as-
then the mathematical expectation can be defined as-

The expected value of a random variable X is written as E(X).
Expected value for a continuous random variable is

Q2) Find the expectations of the number of an unbiased die when thrown.
A2)
Let X be a random variable which represents the number on a die when thrown.
X can take the values-
1, 2, 3, 4, 5, 6
With
P[X = 1] = P[X = 2] = P[X = 3] = P[X = 4] = P[X = 5] = P[X = 6] = 1/6
The distribution table will be-
X | 1 | 2 | 3 | 4 | 5 | 6 |
p(x) | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Hence the expectation of number on the die thrown is-
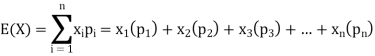
So that-

Q3) What are moments?
A3)
In Statistics, moments are the arithmetic means of first, second, third and so on, i.e. rth power of the deviation taken from either mean or an arbitrary point of a distribution. In other words, moments are statistical measures that give certain characteristics of the distribution. In statistics, some moments are very important. Generally, in any frequency distribution, four moments are obtained which are known as first, second, third and fourth moments. These four moments describe the information about mean, variance, skewness and kurtosis of a frequency distribution. Calculation of moments gives some features of a distribution which are of statistical importance. Moments can be classified in raw and central moment. Raw moments are measured about any arbitrary point A (say). If A is taken to be zero then raw moments are called moments about origin. When A is taken to be Arithmetic mean we get central moments. The first raw moment about origin is mean whereas the first central moment is zero. The second raw and central moments are mean square deviation and variance, respectively. The third and fourth moments are useful in measuring skewness and kurtosis.
The rth moment of a variable x about the mean x is usually denoted by is given by

The rth moment of a variable x about any point a is defined by
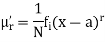




Q4) Define Chebyshev’s inequality.
A4)
If X is any random variable then for any b>0 we have

Chebyshev’s inequality states that the difference between X and EX is somehow limited by Var (X). This is intuitively expected as variance shows on average how far we are from the mean.
Q5) Let X be a random variables such that

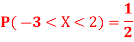
Find a lower bound to its variance.
A5)
The lower bound can be derived thanks to Chebyshev’s inequality
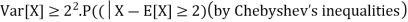
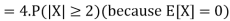
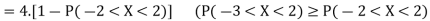
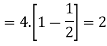
Thus, the lower bound is Var[X]≥2
Q6) A individual is selected from a population randomly who has average income of 40,000 dollars with SD 20,000 dollars, what will be the probability of selecting an individual whose income is either less than 10,000 dollars or greater than 70,000 dollars.
A6)
Here we use Chebyshev inequality to solve such problems.
If X denotes income then X is less than 10,000 dollars or greater than 70,000 dollars only if-

Where 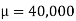 and b = 30,000 the the probability-
and b = 30,000 the the probability-
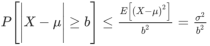
= 400,000,000/900,000,000 = 4/9
Q7) Find the moment generating function of the exponential distribution  . Hence find its mean and S.D.
. Hence find its mean and S.D.
A7)
The moment generating function about the origin is
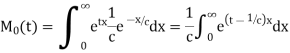
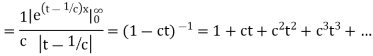
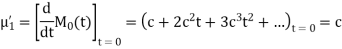
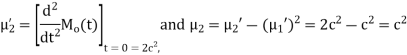
Hence the mean is c wand S.D. Is also c
Q8) What do you understand by conditional expectations?
A8)
Let X and Y be two random variables. The conditional expectation of X given Y = y is the weighted average of the values that X can take on, where each possible value is weighted by its respective conditional probability (conditional on the information that Y = y
The expectation of a random variable X conditional on Y = y is given by E[X|Y = y]
In the case in which X and Y are two discrete random variables and, considered together, they form a discrete random vector the formula for computing the conditional expectation of X given Y = y is a straightforward implementation of the above informal definition of conditional expectation: the weights of the average are given by the conditional probability mass function of X.
Definition Let X and Y be two discrete random variables. Let  be the support of X and let pX|Y-y(X) be the conditional probability mass function of X given Y = y. The conditional expectation of X given Y = y is
be the support of X and let pX|Y-y(X) be the conditional probability mass function of X given Y = y. The conditional expectation of X given Y = y is
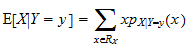
Provided that
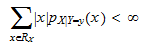
Q9) Find the mean of the following dataset.
x | 20 | 30 | 40 |
f | 5 | 6 | 4 |
A9)
We have the following table-
X | F | Fx |
20 | 5 | 100 |
30 | 6 | 180 |
40 | 7 | 160 |
| Sum = 15 | Sum = 440 |
Then Mean will be-
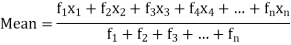

Q10) Find the median of the following dataset-

A10)
Class interval | Frequency | Cumulative frequency |
0 - 10 | 3 | 3 |
10 – 20 | 5 | 8 |
20 – 30 | 7 | 15 |
30 – 40 | 9 | 24 |
40 – 50 | 4 | 28 |

So that median class is 20-30.
Now putting the values in the formula-

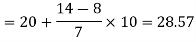
So that the median is 28.57
Q11) Find the mode from the following data)
Age | 0-6 | 6-12 | 12-18 | 18-24 | 24-30 | 30-36 | 36-42 |
Frequency | 6 | 11 | 25 | 35 | 18 | 12 | 6 |
A11)
Age | Frequency | Cumulative frequency |
0-6 6-12 12-18  24-30 30-36 36-42 | 6 11 25  35 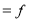   12 6 | 6 17 42 77 95 107 113 |
Mode
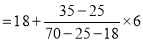

Q12) Find the quartile deviation of the following data-
Class interval | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
Frequency | 3 | 5 | 7 | 9 | 4 |
A12)
Here N/4 = 28/4 = 7 so that the 7’th observation falls in class 10 – 20.
And
3N/4 = 21, and 21’st observation falls in the interval 30 – 40 which is the third quartile.
The quartiles can be calculated as below-
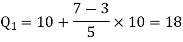
And
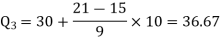
Hence the quartile deviation is-
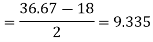
Q13) Find the mean deviation from the mean of the following data-
Class interval | 0-6 | 6-12 | 12-18 | 18-24 | 24-30 |
Frequency | 8 | 10 | 12 | 9 | 5 |
A13)
Class interval | Mid-value | Frequency | d = x – a | f.d | |x - 14| | f |x - 14| |
0-6 | 3 | 8 | -12 | -96 | 11 | 88 |
6-12 | 9 | 10 | -6 | -60 | 5 | 50 |
12-18 | 15 | 12 | 0 | 0 | 1 | 12 |
18-24 | 21 | 9 | 6 | 54 | 7 | 63 |
24-30 | 27 | 5 | 12 | 60 | 13 | 65 |
Total |
| 44 |
| -42 |
| 278 |
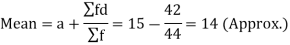
Then mean deviation from mean-

Q14) What is standard deviation?
A14)
It is defined as the positive square root of the arithmetic mean of the square of the deviation of the given values from their arithmetic mean. It is denoted by the symbol 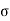 .
.
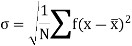
Where  is A.M of the distribution
is A.M of the distribution  . We have more formulae to calculate the standard deviation.
. We have more formulae to calculate the standard deviation.
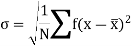
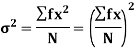
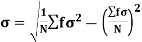 ….
…. 
In frequency distribution from, we put  where H is generally taken as width of class interval
where H is generally taken as width of class interval


Shortcut formula to calculate standard deviation-

The square of the standard deviation is called known as a variance.

Q15) Calculate the standard deviation of the following frequency distribution-
Weight | 60 – 62 | 63 – 65 | 66 – 68 | 69 – 71 | 72 – 74 |
Item | 5 | 18 | 42 | 27 | 8 |
A15)
Weight | Item (f) | X | d = x – 67 | f.d | 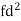 |
60 – 62 | 5 | 61 | -6 | -30 | 180 |
63 – 65 | 18 | 64 | -3 | -54 | 162 |
66 – 68 | 42 | 67 | 0 | 0 | 0 |
69 – 71 | 27 | 70 | 3 | 81 | 243 |
72 – 74 | 8 | 73 | 6 | 48 | 288 |
Total |
100 |
|
|
45 |
873 |