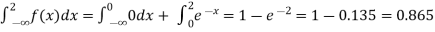Unit - 3

Special probability distributions

Q1) Find the mean and variance of a number on an unbiased die when thrown.

A1)

Suppose X be the number on an unbiased die when thrown,

Then X can take the values 1, 2, 3, 4, 5, 6 with

By uniform distribution, we have

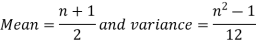
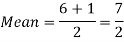
And

Q2) Define Binomial distribution.

A2)

To find the probability of the happening of an event once, twice, thrice,…r times ….exactly in n trails.

Let the probability of the happening of an event A in one trial be p and its probability of not happening be 1 – p – q.

We assume that there are n trials and the happening of the event A is r times and its not happening is n – r times.

This may be shown as follows

AA……A                                 

r times                                       n – r times                          (1)

A indicates its happening its failure and P (A) =p and P (

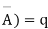
We see that (1) has the probability

Pp…p qq….q=

r times              n-r times                                                       (2)

Clearly (1) is merely one order of arranging r A’S.

The probability of (1) =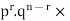Number of different arrangements of r A’s and (n-r)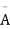’s

The number of different arrangements of r A’s and (n-r)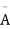’s

Probability of the happening of an event r times =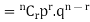

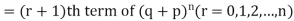
If r = 0, probability of happening of an event 0 times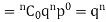

If r = 1,probability of happening of an event 1 times

If r = 2,probability of happening of an event 2 times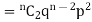

If r = 3,probability of happening of an event 3 times 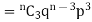and so on.

These terms are clearly the successive terms in the expansion of

Hence it is called Binomial Distribution.

Q3) If on an average one ship in every ten is wrecked. Find the probability that out of 5 ships expected to arrive, 4 at least we will arrive safely.

A3)

Out of 10 ships one ship is wrecked.

I.e. nine ships out of 10 ships are safe, P (safety) =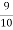

P (at least 4 ships out of 5 are safe) = P (4 or 5) = P (4) + P(5)

Q4) The probability that a man aged 60 will live to be 70 is 0.65. What is the probability that out of 10 men, now 60, at least seven will live to be 70?

A4)

The probability that a man aged 60 will live to be 70

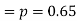
Number of men= n = 10

Probability that at least 7 men will live to 70 = (7 or 8 or 9 or 10)

= P (7)+ P(8)+ P(9) + P(10) =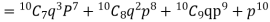

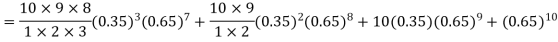
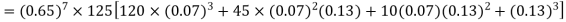
Q5) Derive SD of Binomial distribution.

A5)

Successors r	Frequency f
0		0
1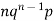
2		2n(n-1)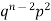
3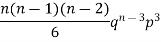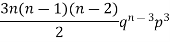
…..	……	….
n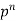

We know that           (1)

r is the deviation of items (successes) from 0.

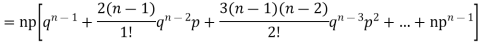
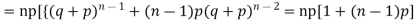
Putting these values in (1) we have

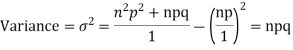
Q6) A die is tossed thrice. A success is getting 1 or 6 on a TOSS. Find the mean and variance of the number of successes.

A6)

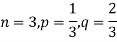
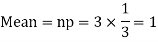
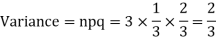
Q7) What is the recurrence relationship of binomial distribution?

A7)

By Binomial Distribution

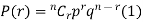
On dividing (2) by (1) , we get

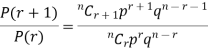
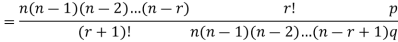
Q8) What is negative binomial distribution?

A8)

Negative binomial distribution is a probability distribution of number of occurences of successes and failures in a sequence of independent trails before a specific number of success occurs. Following are the key points to be noted about a negative binomial experiment.

1. The experiment should be of x repeated trials.
2. Each trail have two possible outcome, one for success, another for failure.
3. Probability of success is same on every trial.
4. Output of one trial is independent of output of another trail.
5. Experiment should be carried out until r successes are observed, where r is mentioned beforehand.

Negative binomial distribution probability can be calculated by using-

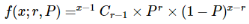
Where −

1. x = Total number of trials.
2. r  = Number of occurrences of success.
3. P = Probability of success on each occurence.
4. 1−P= Probability of failure on each occurence.
5. f(x;r,P)= Negative binomial probability, the probability that an x-trial negative binomial experiment results in the rth success on the xth trial, when the probability of success on each trial is P.
6. NCr = Combination of n items taken r at a time.

Q9) Define geometric distribution.

A9)

The geometric distribution is a special case of the negative binomial distribution. It deals with the number of trials required for a single success. Thus, the geometric distribution is a negative binomial distribution where the number of successes (r) is equal to 1.

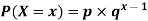
Where −

1. p = probability of success for single trial.
2. q = probability of failure for a single trial (1-p)
3. x = the number of failures before a success.
4. P(X−x) = Probability of x successes in n trials.

Q10) What is the hyper-geometric distribution?

A10)

When the population is finite and the sampling is done without replacement, so that the events are stochastically dependent, although random, we obtain hyper-geometric distribution.

Suppose a urn contains N balls, of which M are white and N-M are black.

Of these, n balls are chosen at random without replacement. Let X be a random variable that denote the number of white balls drawn. Then, the probability of X = x white balls among the n balls drawn is given by

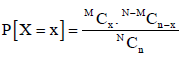
[For x = 0, 1, 2,..., n (n 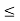M) or x = 0, 1, 2,...,M (n > M)]

The probability function of discrete random variable X given above is known as the Hyper-geometric distribution.

Q11) What is Poisson distribution.

A11)

Poisson distribution is a particular limiting form of the Binomial distribution when p (or q) is very small and n is large enough.

Poisson distribution is

Where m is the mean of the distribution.

Proof. In Binomial Distribution

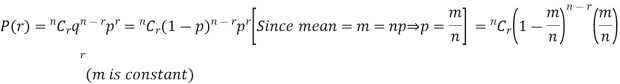
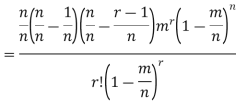
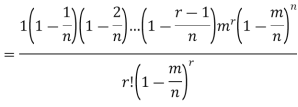
Taking limits when n tends to infinity

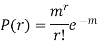
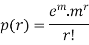
Q12) Show that in a Poisson distribution with unit mean, and the mean deviation about the mean is 2/e times the standard deviation.

A12)

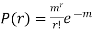But mean = 1 i.e. m =1 and S.D. =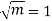

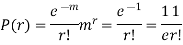
r	P (r)	|r-1|	P(r)|r-1|
0		1
1		0	0
2		1
3		2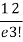
4		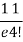3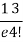
…..	…..	…..	…..
r		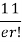r-1

Mean Deviation =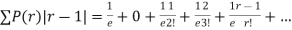

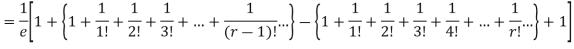
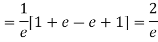
Q13) Give the expression of cumulative generating function of Poisson distribution.

A13)

The cumulant generating function is given by

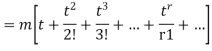
Now cumulant =coefficient of in K (t) = m

i.e. 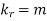, where r = 1,2,3,…

Mean =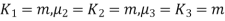

Q14) Assume that the probability of an individual coal miner being killed in a mine accident during a year is . Use appropriate statistical distribution to calculate the probability that in a mine employing 200 miners, there will be at least one fatal accident in a year.

A14)

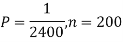
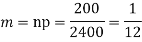
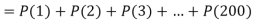
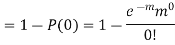
Q15) In a certain factory producing cycle tyres, there is a smallchance of 1 in 500 tyres to be defective. The tyres are supplied in lots of 10. Using Poisson distribution, calculate the approximate number of lots containing no defective, one defective and two defective tyres, respectively, in a consignment of 10,000 lots.

A15)

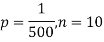
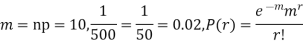
S.No.	Probability of defective	Number of lots containing defective
1.
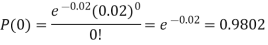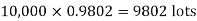2.
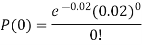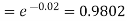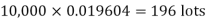3.

Q16) A die weighed or loaded so that the number of spots X that appear on the up face when the die is rolled has pmf

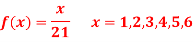
If this loaded die is rolled 21 times. Find the probability of rolling one one, two twos, three threes, four fours, five fives, six sixes.

A16)

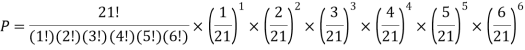
Q17) If we have 10 balls in a bag, in which 2 are red, 3 are green and remaining are blue colour balls. Then we select 4 balls randomly form the bag with replacement, then what will be the probability of selecting 2 green balls and 2 blue balls.

A17)

Here this experiment has 4 trials so n = 4.

The required probability will be-

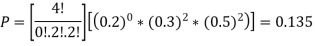
So that-

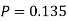
Q18) Buses are scheduled every 5 minutes at a certain bus stand. A person comes to the stand at a random time. Let the random variable X count the number of minutes he/she has to wait for the next bus. Assume X has a uniform distribution over the interval (0, 5). Find the probability that he/she has to wait at least 3 minutes for the bus.

A18)

As X follows uniform distribution over the interval (0, 5), probability density function of X is

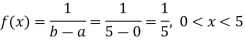
Thus, the desired probability

The probability that he/she has to wait at least 3 minutes for the bus is 0.4.

Q19) I choose real number uniformly at random in the interval [a, b], and call it X. Buy uniformly at random, we mean all intervals in [a, b] that have the same length must have the same probability. Find the CDF of X.

A19)

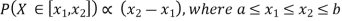
Since 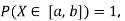we conclude

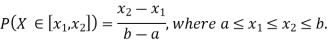
Now, let us find the CDF. By definition 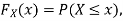thus immediately have

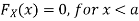
For

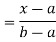
Thus, to summarize

Note that hear it does not matter if we use “<” or “≤” as each individual point has probability zero, so for example Figure 4.1 shows the CDF of X. As we expect the CDF starts at 0 at end at 1.

Q20) What do you understand by chi-square distribution?

A20)

When a fair coin is tossed 80 times we expect from the theoretical considerations that heads will appear 40 times and tail 40 times. But this never happens in practice that is the results obtained in an experiment do not agree exactly with the theoretical results. The magnitude of discrepancy between observations and theory is given by the quantity (pronounced as chi squares). If 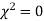the observed and theoretical frequencies completely agree. As the value of 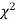increases, the discrepancy between the observed and theoretical frequencies increases.

(1)  Definition. If and be the corresponding set of expected (theoretical) frequencies, then 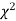is defined by the relation

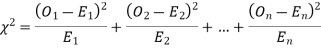
(2)  Chi – square distribution

If be n independent normal variates with mean zero and s.d. Unity, then it can be shown that is a random variate having 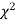distribution with ndf.

The equation of the curve is

Q21) A set of five similar coins is tossed 320 times and the result is

A21)

For v = 5, we have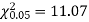

P, probability of getting a head=1/2; q, probability of getting a tail=1/2.

Hence the theoretical frequencies of getting 0,1,2,3,4,5 heads are the successive terms of the binomial expansion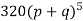

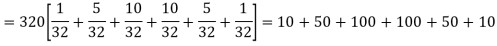
Thus the theoretical frequencies are 10, 50, 100, 100, 50, 10.

Hence,

Since the calculated value of is much greater than the hypothesis that the data follow the binomial law is rejected.

Q22) What is normal distribution?

A22)

Normal distribution is a continuous distribution. It is derived as the limiting form of the Binomial distribution for large values of n and p and q are not very small.

The normal distribution is given by the equation

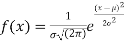    (1)

Where = mean, 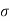= standard deviation, 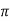=3.14159…e=2.71828…

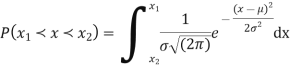
On substitution 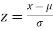in (1) we get      (2)

Here mean = 0, standard deviation = 1

(2) is known as standard form of normal distribution.

MEAN FOR NORMAL DISTRIBUTION

Mean 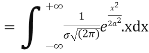        [Putting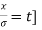

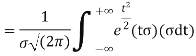
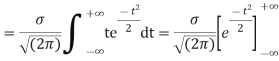
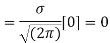
STANDARD DEVIATION FOR NORMAL DISTRIBUTION

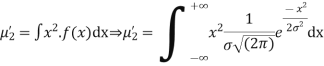
Put,

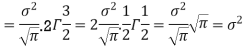
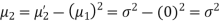
Q23) Find the area under the normal curve in each of the cases

(a)  Z = 0 and z = 1.2

(b)  Z = -0.68 and z = 0

(c)  Z = -0.46 and z = -2.21

(d)  Z = 0.81 and z = 1.94

(e)  To the left of z = -0.6

Right of z = -1.28

A23)

(a) Area between Z = 0 and z = 1.2 =0.3849

(b)Area between z = 0 and z = -0.68 = 0.2518

(c)Required area = (Area between z = 0 and z = 2.21) + (Area between z = 0 and z =-0.46)\

= (Area between z = 0 and z = 2.21)+ (Area between z = 0 and z = 0.46)

=0.4865 + 0.1772 = 0.6637

(d)Required area = (Area between z = 0 and z = 1.+-(Area between z = 0 and z = 0.81)

= 0.4738-0.2910=0.1828

(e) Required area = 0.5-(Area between z = 0 and z = 0.6)

= 0.5-0.2257=0.2743

(f)Required area = (Area between z = 0 and z = -1.28)+0.5

= 0.3997+0.5

= 0.8997

Q24) A manufacturer knows from experience that the resistance of resistors he produces is normal with mean and standard deviation . What percentage of resistors will have resistance between 98 ohms and 102 ohms?

A24)

,

Area between

= (Area between z = 0 and z = +1)

= 2 (Area between z = 0 and z = +1)=2 0.3413 = 0.6826

Percentage of resistors having resistance between 98 ohms and 102 ohms = 68.26

Q25) Let be two independent N (0, 1) random variables. Define

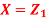
Where is a real number in (-1, 1).

1. Show that X and Y are bivariate normal.
2. Find the joint PDF of X and Y.
3. Find (X,Y)

A25)

First note that since 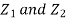are normal and independent they are jointly normal with the joint PDF

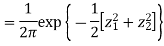
1. We need to show aX + bY is normal for all. We have

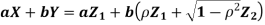
Which is the linear combination of 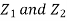and thus it is normal.

b.     We can use the method of transformations (theorem 5.1) to find the joint PDF of X and Y. The inverse transformation is given by

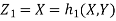
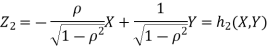
We have

Where,

Thus we conclude that

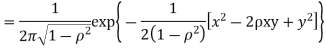
c.      To find FIRST NOTE

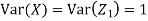
Therefore,

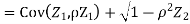
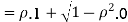
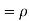
Q26) Find the probability distribution of the number of heads when three coins are tossed simultaneously.

A26)

Let be the number of heads in the toss of three coints

The sample space will be-

{HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}

Here variable X can take the values 0, 1, 2, 3 with the following probabilities-

P[X= 0] = P[TTT] = 1/8

P[X = 1] = P [HTT, THH, TTH] = 3/8

P[X = 2] = P[HHT, HTH, THH] = 3/8

P[X = 3] = P[HHH] = 1/8

Hence the probability distribution of X will be-

X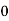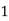
P(x)

Q27)

(i)                Is the function defined as follows a density function.

(ii)             If so determine the probability that the variate having this density will fall in the interval (1.2).

(iii)          Also find the cumulative probability function F (2)?

A27)

(i) f (x) is clearly ≥0 for every x in (1,2) and

Hence the function f (x) satisfies the requirements for a density function.

(ii)Required probability =

This probability is equal to the shaded area in figure 26.3 (a).

(iii)Cumulative probability function F(2)