Unit - 1
Automorphism
Q1) What is automorphism?
A1)
The automorphism group is the collection of all an object's automorphisms. It is, in a broad sense, the object's symmetry group.
In mathematics, an automorphism is an isomorphism between two mathematical objects. In some aspects, it's a symmetry of the thing, as well as a method of mapping the object to itself while maintaining all of its structure. All of an object's automorphisms are collected in the automorphism group. It is, in a general sense, the symmetry group of the item.
• In set theory, an automorphism is an arbitrary permutation of the elements of a set X. The symmetric group on X is sometimes known as the automorphism group of X. The set of integers Z, viewed as a group under addition in elementary arithmetic, has a single nontrivial automorphism: negation. However, when viewed as a ring, it merely has the trivial automorphism. Negation is a word that is used to express the absence of something.
Q2) What is inner automorphism?
A2)
In abstract algebra an inner automorphism is an automorphism of a group, ring, or algebra given by the conjugation action of a fixed element, called the conjugating element. These inner automorphisms form a subgroup of the automorphism group, and the quotient of the automorphism group by this subgroup gives rise to the concept of the outer automorphism group.
If G is a group and g is an element of G (alternatively, if G is a ring, and g is a unit), then the function
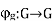
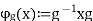
g refers to this as (right) conjugation (see also conjugacy class). For every, this function is an endomorphism of G:
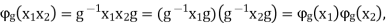
Where the second equality is given by the insertion of the identity between X1 and X2 Furthermore, it has a left and right inverse, namely 
Thus, 
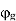is bijective, and so an isomorphism of G with itself, i.e. an automorphism. An inner automorphism is any automorphism that arises from conjugation.
When discussing right conjugation, the expression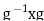 
is often denoted exponentially by 
This notation is used because composition of conjugations satisfies the identity: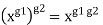 
for all 
This shows that conjugation gives a right action of G on itself.
Q3) What are different types automorphism?
A3)
If an object's automorphisms constitute a set (rather than a proper class), they form a group under morphism composition. The automorphism group of X is the name given to this group.
Closure
Another automorphism is the composition of two automorphisms.
Associativity
The associative nature of morphism composition is part of the notion of a category.
Identity
The identity morphism from an item to itself, which is an automorphism, is called the identity.
Inverses
Every isomorphism has an inverse, which is also an isomorphism, and the inverse is an automorphism because it is also an endomorphism of the same object.
If the category C is evident from context, the automorphism group of an object X in that category is called AutC(X), or simply Aut(X).
Q4) Explain the infinite cyclic group?
A4)
An infinite cyclic group is a cyclic group G such that
An infinite cyclic group is a cyclic group G such that:
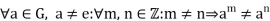
Where e denotes G's identity element.
That is, so that all of a's powers are distinct.
An infinite cyclic group is represented as follows:
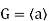
This states that G is generated by a single infinite-order element.
The additive group of integers (Z,+) creates an infinite cyclic group from Integers under Addition form Infinite Cyclic Group. As a result, the infinite cyclic group is frequently denoted by the letter Z. This is supported by the fact that, according to Cyclic Groups of the Same Order are Isomorphic, Z is isomorphic to a.
Q5) Prove the statement “. A finitely generated group G has a finite automorphism group if and only if it has a central cyclic subgroup of finite index.”
A5)
PROOF: First, we'll show that these requirements are sufficient. We can assume that G is infinite and so a finite and central extension of an infinite cyclic group if we do so. The centre Z of G has a finite index in G, hence it is finitely generated according to Schreier's subgroup theorem. As a result, Z is the direct sum of an infinite cyclic group and a finite abelian group T. As a result, Hom(G/if, Z) = HomGjZ, T) and Aut(G/Z) are finite. Finally, once we prove that Aut(Z) is finite, we can use the following Corollary. This, however, is the result of another application of the Corollary. If Aut(G) is finite, then GZ is finite because it is isomorphic to G's inner automorphism group. Z will be finitely generated again, thanks to Schreier's theorem. In opposition to the theorem, we can assume that Z contains two or more infinite cyclic components in a direct decomposition into cyclic groups. Let Z = W x () x (6) be the subgroups produced by components a and b, respectively. Write ma> = wa> + rta + ta>b for the factor set M, where w>e W, sa>, and ta> are all integers. Let (w) = wor w W, (a) = ma + rib, (b) = pa + qb be the automorphism of Z, where m,n,p, and q are all integers, and mq— np = 1. The factor set (M) can thus be expressed as (ma) = wt + s r.a + t'b, where s'a =msΛtβ + ptob3 and Vatβ = nsa>β +
QtΛtβ. As a result, So = s>, To = tat, SO = s, and To = trt are GZ factor sets with integral values, and SQ — mS0 + pT0, To = nS0 + qT0. The proof is now reduced to the following problem by Lemmas 1 and 2: Find as many quadruplets (m, n, p, q) of integers as possible.| The factor sets mS0 + pT0 and nS0 + qT0 are equal to the factor sets So and To, respectively, and mq — np = 1. To put it another way, the factor sets (m —)SO + pT0 and nS0 + (q —)T0 are both trivial factor sets. If GjZ has orderh, however, hS0 and hT0 are both equal to the trivial factor set (3; p. 223).
As a result, the following values for m, n, p, and q suffice for any integer k: h p = -h2 k -hk2 -h q = hk + l m = -h2 - hk + 1 n — h p = -h2 k -hk2 -h q = hk + l m = -h2 - hk + 1 n — h p = -h2 k -hk2 -h q
Q6) Explain the Fully characteristic subgroup?
A6)
A fully characteristic subgroup (also, fully invariant subgroup; cf. Invariant subgroup), H, of a group G is a group that remains invariant under every endomorphism of G; that is, a fully characteristic subgroup (also, fully invariant subgroup; cf. Invariant subgroup) of G is a group that remains invariant under every endomorphism of G.
∀φ∈End(G)：φ[H] ≤ H.
Every group has two fully distinctive subgroups: itself (the inappropriate subgroup) and the trivial subgroup. A fully characteristic subgroup is always the commutator subgroup of a group. [3] [4]
Every G endomorphism produces a G/H endomorphism, resulting in a map End(G) End(G/H).
Q7) What are Virtually cyclic groups?
A7)
If a group contains a finite index cyclic subgroup, it is said to be virtually cyclic (the number of cosets that the subgroup has). To put it another way, each element in a nearly cyclic group can be obtained by multiplying a cyclic subgroup member with a member of a finite set. Every cyclic group, like every finite group, is nearly cyclic. The direct product of Z/nZ and Z, in which the factor Z has finite index n, is an example of an infinite group that is nearly cyclic if and only if it is finitely produced and has exactly two ends. A Gromov hyperbolic group's abelian subgroups are all virtually cyclic.
Q8) What are the cyclic group?
A8)
A cyclic group or monogenous group is a group produced by a single element in n group theory, a branch of abstract algebra. It's a collection of invertible items with a single associative binary operation, in other words.and it contains an element g such that by repeatedly applying the group operation to g or its inverse, every other element of the group may be obtained. Each element can be expressed as a multiple of g in additive notation or as a power of g in multiplicative notation. The element g is referred to as a group generator. Every infinite cyclic group is isomorphic to Z, the integers' additive group. The additive group of Z/nZ, the integers modulo n, is isomorphic to any finite cyclic group of rank n. Every cyclic group is an abelian group (i.e., it has a commutative group operation), and every finitely produced abelian group is a direct product of cyclic groups.Every prime-order cyclic group is a simple group that cannot be subdivided into smaller ones. The cyclic groups of prime order are one of the three infinite classes in the classification of finite simple groups. The prime order cyclic groups are thus among the basic blocks from which all groups can be constructed.
Q9) What are symmetric group?
A9)
The symmetric group defined over any set in abstract algebra is the group whose elements are all the bijections from the set to itself and whose group operation is function composition. The permutations that can be done on the n symbols make up the finite symmetric group defined over a finite set of n symbols. Because there are ( factorial) permutations,
Despite the fact that symmetric groups can be created on infinite sets, this article focuses on finite symmetric groups, including their applications, elements, conjugacy classes, finite presentations, subgroups, automorphism groups, and representation theory. The term "symmetric group" will be used throughout this text to refer to a symmetric group on a finite set.
The symmetric group is useful in a variety of areas of mathematics, including Galois theory, invariant theory, Lie group representation theory, and combinatorics. Every group G is isomorphic to a subgroup of the symmetric group on (the underlying set of) G, according to Cayley's theorem.
Q10) What are Locally cyclic groups and Cyclically ordered groups?
A10)
Locally cyclic groups
A locally cyclic group is one whose finitely produced subgroups are all cyclic. The additive group of rational numbers, for example, is a set of integer multiples of a single unit fraction, the inverse of their lowest common denominator, which forms a cyclic group of integer multiples of this unit fraction as a subgroup. Locally, a group is cyclic.
Cyclically ordered groups
A cyclically ordered group is one that has a cyclic order that is maintained by the group structure. Every cyclic group can be given a structure that is consistent with the ordering of the integers as a cyclically ordered group (or the integers modulo the order of the group). A cyclically ordered
Q11) The automorphism ϕ is the identity on real numbers.
A11)
In this claim, we finish the proof of the problem.
Let x be any positive integer.
Seeking a contradiction, assume that ϕ(x)≠x.
Consider the following two scenarios:
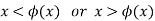
First, suppose that x<ϕ(x). Then there is a rational number q that is equal to
Then there's
ϕ(x)<ϕ(q) by Claim 2 since x<q
= Claim 4 applies to q because q is reasonable.
<ϕ(x) by the choice of q,
This is an inconsistency. Consider the following scenario. When x>ϕ(x).
There is a rational number q that has the property of
Then, using the same logic as before, we arrive at
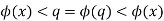
Which is a contradiction. As a result, in any instance, we arrived at a contradiction, and as a result,
We must have ϕ(x)=x for all real numbers x. This proves that the automorphism ϕ: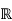
→
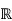is the identity map.
Q12) Determine the automorphism group of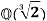 
over Q.
A12)
Let σ∈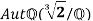
be an automorphism of 
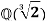over Q.
Then σ is determined by the value σ(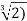
since any element α of 
can be written as 
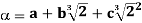for some a,b,c∈
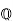and
=
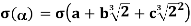
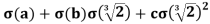
Because Q's elements are σ fixed
Note that σ(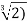
is a root of the minimal polynomial 
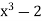and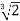
.
But the roots of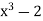 
are not real except 
, hence not in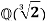 
.
Thus we must have σ(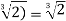
.
Hence σ is trivial.
In conclusion, we have
Q13) Let H be a subgroup of a group G. We call H characteristic in G if for any automorphism σ∈Aut(G), we have σ(H)=H.
(a) Prove that if σ(H)⊂H for all σ∈Aut(G), then H is characteristic in G.
A13)
(a) If σ(H)⊂H for all σ∈Aut(G), then H is characteristic in G
Since σ is an automorphism, the inverse σ−1 is also an automorphism of G.
Hence, we have
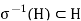
By the assumption.
Applying σ, we have
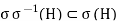
Then we obtain
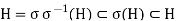
Since the both ends are H, the inclusion is in fact the equality.
Thus, we obtain
And the subgroup H is characteristic in the group G.
Q14) Let H be a subgroup of a group G. We call H characteristic in G if for any automorphism σ∈Aut(G), we have σ(H)=H.
(b) The center Z(G) of G is characteristic in G
A14)
By part (a), it suffices to prove that σ(Z(G))⊂Z(G) for every
Automorphism σ∈Aut(G) of G.
Let x∈σ(Z(G)). Then there exists y∈Z(G) such that x=σ(y).
To show that x∈Z(G), consider an arbitrary g∈G.
Then since σ is an automorphism, we have G=σ(G).
Thus there exists g′ such that g=σ(g′).
We have
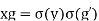
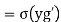(since is a homomorphism)
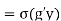(since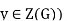 
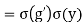(since is a homorphism)
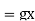
Since this is true for all g∈G, it follows that x∈Z(G), and thus
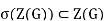
This completes the proof.
Q15) Prove the followings.
(a) If H is characteristic in G, then H is a normal subgroup of G.
A15)
For each g∈G, define a map ϕg:G→G defined by ϕg(x)=gxg−1. This is an automorphism of G with the inverse ϕg−1.
Since H is characteristic, we have ϕg(H)=H, equivalently we have gHg−1=H.
Therefore H is a normal subgroup of G.
Q16) Prove the followings.
(b) If H is the unique subgroup of G of a given order, then H is characteristic in G.
A16)
For any automorphism ϕ∈Aut(G), we have ϕ(H)⊂ϕ(G)=G and |H|=|ϕ(H)|. The uniqueness of H implies that H=ϕ(H) and thus H is characteristic.
Q17) Prove the followings.
(c) Suppose that a subgroup K is characteristic in a group H and H is a normal subgroup of G. Then K is a normal subgroup in G.
A17)
For each g∈G, consider the automorphism ϕg of G defined in the proof of (a).
Since H◃G, we have ϕg(H)=H.
Hence the restriction ϕg|H belongs to Aut(H).
Now since K is characteristic in H, we have ϕg|H(K)=K, or equivalently we have gKg−1=K and K is normal in G.
Q18) Give an example of a semigroup without an identity element.
A18)
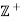= {1, 2, 3, ...} is a semigroup without identity with binary operation usual addition.
Q19) Give an example of an infinite semigroup with an identity element e such that no element except e has an inverse.
A19)
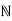= {0, 1, 2, ...} is a semigroup with binary operation usual addition. No non-identity element has an inverse.
Q20) Let S be a semigroup and let x ∈ S. Show that {x} forms a subgroup of S (of order 1) if and only if x 2 = x such an element x is called idempotent in S.
A20)
Assume that {x} forms a subgroup. Then {x}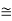 
{1} and x 2 = x.
Conversely assume that x 2 = x. Then associativity is inherited from S. So Identity element of the set {x} is itself and inverse of x is also itself. Then {x} forms a subgroup of S.
