Unit - 3
Group actions
Q1) What are group action? Explain the left group action?
A1)
A group action on a space in mathematics is a group homomorphism of a given group into the space's group of transformations. A group action on a mathematical structure is the same as a group homomorphism of a group into the structure's automorphism group. The group is believed to have an effect on the space or structure. When a group operates on a structure, it almost always acts on the objects that are created from that structure.
A (left) group action of G on X is a function if G is a group with identity element e and X is a set.

(with α(g, x) often shortened to gx or g ⋅ x when the action being considered is clear from context)
That satisfies the following two axioms:
Identity: 
Compatibility: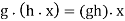
For all g and h in G, as well as all x in X
The G group is considered to be influenced by X. (from the left). A (left) G-set is a combination of a set X and a G action.
From these two axioms, it follows that the function from X to itself that maps x to g x is a bijection for any fixed g in G, with inverse bijection being the corresponding map for g1. As a result, a group action of G on X can be defined as a group homomorphism from G to the symmetric group Sym(X) of all bijections from X to itself.
Q2) Explain the right group action? And difference between left and right group?
A2)
a right group action of G on X is a function
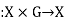
(with α(x, g) often shortened to xg or x ⋅ g when the action being considered is clear from context)
That satisfies the analogous axioms:
Identity: 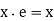
Compatibility: 
For all g and h in G and all x in X.
The difference between left and right actions is in the order in which a product gh acts on x. For a left action, h acts first, followed by g second. For a right action, g acts first, followed by h second. Because of the formula (gh)−1 = h−1g−1 By composing with the group's inverse operation, a left action can be created from a right action. A right action of a group G on X can also be thought of as a left action of the opposite group Gop on X.
As a result, considering solely left actions is sufficient for proving general features of group actions.
Q3) Explain the Cayley's theorem?
A3)
Cayley's theorem, named for Arthur Cayley, states that any group G is isomorphic to a subgroup of the symmetric group acting on G in group theory. This might be interpreted as an illustration of G's group action on G's constituents. The theorem can be proved by explicitly creating the representation within the regular representation of the symmetric group of permutation matrices.
A permutation of a set G is any bijective function taking G onto G. The set of all permutations of G forms a group under function composition, called the symmetric group on G, and written as Sym(G).
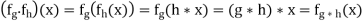
For all x in G, and hence:
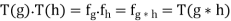
The homomorphism T is injective since T(g) = idG (the identity element of Sym(G)) implies that g ∗ x = x for all x in G, and taking x to be the identity element e of G yields g = g ∗ e = e, i.e. the kernel is trivial. Alternatively, T is also injective since g ∗ x = g′∗ x implies that g = g′ (because every group is cancellative).
As a result, G is isomorphic to T, which is the subgroup K.
The normal representation of G is sometimes referred to as T.
Q4) Explain the index theorem?
A4)
The number of left cosets of H in G, or equivalently, the number of right cosets of H in G, is the index of a subgroup H in a group G in mathematics, specifically group theory. The index is denoted 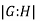 or [G:H] or (G:H). Because G is the disjoint union of the left cosets and because each left coset has the same size as H, the index is related to the orders of the two groups by the formula
or [G:H] or (G:H). Because G is the disjoint union of the left cosets and because each left coset has the same size as H, the index is related to the orders of the two groups by the formula
(interpret the quantities as cardinal numbers if some of them are infinite). Thus the index [G:H] measures the "relative sizes" of G and H.
For example, let G=Z be the group of integers under addition, and let H=2Z be the subgroup consisting of the even integers. Then 2Z has two cosets in Z, namely the set of even integers and the set of odd integers, so the index 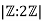 is 2. More generally,
is 2. More generally, 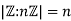 for any positive integer n.
for any positive integer n.
When G is finite, the formula may be written as 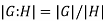 , and it implies Lagrange's theorem that |H| divides |G|.
, and it implies Lagrange's theorem that |H| divides |G|.
When G is infinite, |G:H| is a nonzero cardinal number that may be finite or infinite. For example, |Z:2Z|=2, but |R:Z| is infinite.
Because the underlying set of G/N is the set of G/N cosets of N in G, |G:N| is equal to the order of the quotient group if N is a normal subgroup of G.
Q5) Explain What are Stabilizers?
A5)
Consider the actions of a group G on a set X. The set of elements in X to which an element x can be transported by the elements of G is called the orbit of an element x in X. Gx is the symbol for x's orbit:
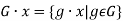
The defining features of a group guarantee that under the action of G, the set of orbits of (points x in) X form a partition of X. If and only if there is a g in G with gx = y, the related equivalence relation is defined as x y. Under this relation, the orbits are the equivalence classes; two elements x and y are equal if and only if their orbits are the same, i.e., Gx = Gy.
If and only if the group action has precisely one orbit, that is, if there is x in X with Gx = X, then it is transitive. If and only if Gx = X for all x in X, this is the case (given that X is non-empty).
The quotient of the action is the set of all orbits of X under the action of G, denoted as X/G (or, less frequently: GX). It is known as the orbit space in geometric settings and the space of coinvariants in algebraic situations, and is denoted XG, in contrast to the invariants (fixed points), which are denoted XG: the coinvariants are a quotient while the invariants are a subset. In group cohomology and group homology, which employ the same superscript/subscript standard, coinvariant terminology and notation are very useful.
Q6) Prove:
Let G be a group whose identity is e.
Let Xbe a set.
Let ϕ:G×X→X be a group action.
Let G0 denote the kernel of ϕ.
Then G0 is a normal subgroup of G.
A6)
Let h∈G0.
|
|
|
|
| H | ∈ |
|
|
| G0 |
|
|
|
|
|
| ↭ |
|
| H | ∈ |
|
|
| {g∈G:∀x∈X:g⋅x=x} |
|
| Definition of Kernel of Group Action |
|
|
| ↭ |
| ∀x∈X: | H | ∈∈ |
|
|
| {g∈G:g⋅x=x}{g∈G:g⋅x=x} |
|
|
|
|
|
| ↭ |
| ∀x∈X: | H | ∈ |
|
|
| Stab(x) |
|
|
|
|
|
| ↭ |
|
| h | ∈ |
|
|
| ⋂x∈XStab(x) |
|
|
|
|
|
| ↭ |
|
| G0 | == |
|
|
| ⋂x∈XStab(x) |
|
|
|
|
From Stabilizer is Subgroup:
Stab(x)≤GStab(x)≤G
Thus G0 is the intersection of subgroups.
By Intersection of Subgroups is Subgroup:
G0≤G
To prove normality it is sufficient to show:
∀g∈G:gG0g−1=G0
Let h∈G0,g∈G be arbitrary.
Then:
|
|
|
|
| (ghg−1)⋅x | = |
|
|
| g⋅(h⋅(g−1⋅x)) |
|
| Group Action Associates with Group Operation: Group Action Axiom GA1GA1 |
|
|
|
|
|
|
| == |
|
|
| g⋅(g−1⋅x) |
|
| Because h∈Stab(g−1⋅x)h∈Stab(g−1⋅x) |
|
|
|
|
|
|
| == |
|
|
| (g⋅g−1)⋅x |
|
| Group Action Associates with Group Operation: Group Action Axiom GA1GA1 |
|
|
|
|
|
|
| == |
|
|
| xx |
|
| e⋅x=xe⋅x=x: Group Action Axiom GA2GA2 |
|
Therefore:
Ghg−1∈G0
So:
GG0g−1⊆G0
Conversely suppose that h∈G0h∈G0.
Then by the above:
h′=g−1hg∈G0
Therefore:
h=gh′g−1∈gG0g−1
And so:
G0⊆gG0g−1
This concludes the proof.
Q7) Explain the Virtual permutation representations?
A7)
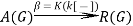
For emphasis, note that linear permutation representations are a minor sub-class of plain linear representations, i.e. a linear representation is not a linear permutation representation in general. However, when we move to virtual representations, this assertion may change dramatically:
If the ring homomorphism β (Def. 2.2) is a surjective function, this means that in fact all virtual linear G-representation are virtual linear permutation representations. This is not the case for all groups, but it is the case for large classes of groups! This is the content of Prop. 3.3 below.
Notice that when this is the case, it signifies that the provided group's representation theory is wholly combinatorial, or, in the context of (1), that it is fully specified over the absolute ground field. F1
Q8) Explain the representation of permutation?
A8)
For G a group (typically a finite group), consider a G-set (S,ρ)), hence a set S (typically a finite set), equipped with an action of G
ρ:G×S⟶S
Equivalently this is a group homomorphism
ρ:G⟶AutSet(S)
From G to the group of permutations of elements of S. As such it is a representation of G “by permutations”.
Specifically, if SS is a finite set and an isomorphism S≃{1,2,3,⋯,n}is understood, it is equivalently a group homomorphism
ρ:G⟶Sn
To the symmetric group Sn on n elements.
This G-action can be linearized to a k-linear representation of G in an obvious fashion for k any field (or, more broadly, any commutative ring, but one usually concerns fields):
Q9) Explain the Brauer relations?
A9)
Permutation representations make ring homomorphism from Burnside ring to representation ring
Since forming k-linear permutation representation is a rig-functor GSet−→−k[−]GRep, under passing to Grothendieck rings it induces a ring homomorphism
K(k[−]):K(GSet,⊔,×)=A(G)−→−−βR(G)=K(GRep,⊕,⊗)
From the Burnside ring of GG to its representation ring.
This homomorphism is traditionally denoted β\beta, as shown.
Its kernel is known as the Brauer relations
Q10) Explain the permutation Associated with a given group action ?
A10)
The linear permutation representation of a G-set (S,ρ)) is the following k-linear representation of G:
- The underlying k-vector space is the freely spanned vector space k[S], whose elements (vectors) are the formal linear combinations
k[S]={v=∑s∈Sfin⊂Svss|Sf infinite sub set, vs∈k}
Of elements of S with coefficients in k, hence is the k-vector space for which S is a canonical linear basis.
2. The linear G-action
k[ρ]:G×k[C]⟶k[C]
Is given on linear basis-elements s∈S↪k[S]s by ρ, which uniquely defines it by linearity to act on a general vector as
k[ρ](g):v↦∑s∈Sfin⊂Svsρ(g)(s).
Q11) Suppose that S is any set and consider G to be any subgroup of A(S). Then G acts on S as follows. For each f ∈ G ⊆ A(S) and each x ∈ S, we define
A11)
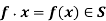
Note that f : S → S is a (bijective) function since f ∈ A(S). Thus this makes sense and condition (0) is verified. For condition (1), note that e ∈ G is the identity function id : S → S, and id .x = id(x) = x as desired. Finally we verify (2), note that if f, g ∈ G, then f.(g.x) = f(g.x) = f(g(x)) = (f ◦ g)(x) = (fg).x as desired.
We now consider the same example in a slightly more explicit framework.
Q12) Suppose that G = S4, the group of permutations on the set S = {1, 2, 3, 4}. We illustrate the action of G on S as in the following examples:
A12)
(a) (12)(34).3=4
(b) (12)(34).2=1
(c) (1234).2=3
(d) (132)(12).2=3
(e) (132)(12).4=4
Finally, we give an example of matrices acting on vectors.
Q13) Assume that G is a set of 22 matrices.

A13)
Under matrix multiplication. These are the matrices that rotate a column vector v clockwise by when multiplied by. This gives us an action of G on  , by A.v = Av. For example, if θ = π/2
, by A.v = Av. For example, if θ = π/2
And 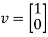 , then consider the matrix acting on the vector
, then consider the matrix acting on the vector
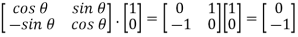
It's simple to confirm that this is a group action. It's worth noting that the identity matrix is in G (corresponding to 0), and the identity matrix sends vectors to itself. It's also worth noting that B.(A.v) = B(Av) = (BA)v = (BA).v, completing the proof.
Q14) Prove that every group of order 24 has a normal subgroup of order 4 or 8.
A14)
Let G be a 24th-order group.
It's worth noting that 24=233.
Assume G has a Sylow 2-subgroup P. Then |P| equals 8.
Consider the operation of the group G via left multiplication on the left cosets G/P.
A permutation representation homomorphism results as a result of this.
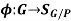
SG/P denotes a collection of bijective maps (permutations) on G/P.
The homomorphism is defined as follows:
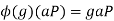
For g∈G and aP∈G/P.
Then by the first isomorphism theorem, we see that
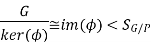
This implies that the order of G/ker(ϕ) divides the order of SG/P. Note that as |G/P|=3, we have |SG/P|=|S3|=6. Thus, we must have 4∣|kerϕ|4∣.
Also note that ker(ϕ)<P. To see this let x∈ker(ϕ). Then we have
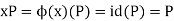
Here id is the identity map from G/P to itself. Hence x∈P. It follows that |ker(ϕ)| divides |P|=8.
Combining these restrictions, we see that |ker(ϕ)|=4,8.
Being the kernel of a homomorphism, ker(ϕ) is a normal subgroup of G.
Hence the group G of order 24 has a normal subgroup of order 4 or 8.
Q15) Let G be a finite group and let S be a non-empty set.
Suppose that G acts on S freely and transitively.
Prove that |G|=|S|. That is, the number of elements in G and S are the same.
A15)
We simply denote by gs the action of g∈G on s∈S.
Since SS is non-empty, we fix an element s0∈S. Define a map
ϕ:G→S
By sending g∈G to gs0∈S.
We prove that the map ϕ is bijective.
Suppose that we have ϕ(g)=ϕ(h) for some g,h∈G.
Then it gives gs0=hs0, and since the action is free this implies that g=h.
Thus ϕ is injective.
To show that ϕ is surjective, let s be an arbitrary element in S.
Since the action is transitive, there exists g∈G such that gs0=s.
Hence we have ϕ(g)=s, and ϕ is surjective.
Therefore the map ϕ:G→S is bijective, and we conclude that |G|=|S|.
Q16) Prove that every finite group of order 72 is not a simple group.
A16)
Observe the prime factorization 72=23⋅32
Let G be a group of order 72.
Let n3 be the number of Sylow 3-subgroups in G.
By Sylow’s theorem, we know that n3 satisfies
n3≡1(mod3) and
n3 divides 8.
The first condition gives n3 could be 1,4,7,…
Only n3=1,4 satisfy the second condition.
Now if n3=1, then there is a unique Sylow 3-subgroup and it is a normal subgroup of order 9.
Hence, in this case, the group G is not simple.
It remains to consider the case when n3=4.
So there are four Sylow 3-subgroups of G.
Note that these subgroups are not normal by Sylow’s theorem.
The group G acts on the set of these four Sylow 3-subgroups by conjugation.
Hence it affords a permutation representation homomorphism
f:G→S4,
Where S4 is the symmetric group of degree 4.
By the first isomorphism theorem, we have
G/kerf<S4.
Thus, the order of G/kerf divides the order of S4.
Since |S4|=4!=23⋅3, the order |kerf| must be divisible by 3 (otherwise |G/kerf| does not divide |S_4|),hence),ker f$ is not the trivial group.
We claim that kerf≠G.
If kerf=G, then it means that the action given by the conjugation by any element g∈G is trivial.
That is, gPg−1=P for any g∈G and for any Sylow 3-subgroup P.
Since those Sylow 3-subgroups are not normal, this is a contradiction.
Thus, kerf≠G.
Since a kernel of a homomorphism is a normal subgroup, this yields that kerf is a nontrivial proper normal subgroup of G, hence G is not a simple group.
Q17) Let p be a prime number. Consider the p th cyclotomic polynomial
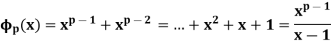
A17)
We claim that Φp(x) is irreducible in  [x]. Although Φp(x) itself does not directly admit application of Eisenstein’s criterion, a minor variant of it does. That is, consider
[x]. Although Φp(x) itself does not directly admit application of Eisenstein’s criterion, a minor variant of it does. That is, consider
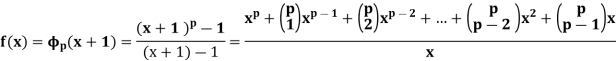
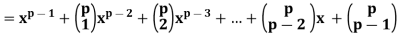
All the lower coefficients are divisible by p, and the constant coefficient is exactly p, so is not divisible by p 2 . Thus, Eisenstein’s criterion applies, and f is irreducible. Certainly if Φp(x) = g(x)h(x) then f(x) = Φp(x + 1) = g(x + 1)h(x + 1) gives a factorization of f. Thus, Φp has no proper factorization.
Q18) Wolfram Alpha says x5−x2+1 is irreducible over 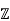 . Is there any way to prove it by Eisenstein's Criterion?
. Is there any way to prove it by Eisenstein's Criterion?
A18)
Eisenstein shift cannot work. But it follows easily from irreducibility mod 2: over F2 it has no roots so no linear factors, so if it splits it has an irreducible quadratic factor g, therefore in
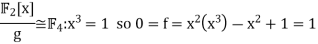
Contradiction.
Q19) Prove that the centralizer of a in G is a subgroup of G.
A19)
Since the identity element e of G satisfies ea=a=ae, it is in the centralizer CG(a).
Hence CG(a) is not an empty set. We show that CG(a) is closed under multiplications and inverses.
Let g,h∈CG(a). Then we have
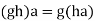
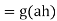 since
since 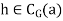
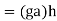
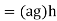 since
since 
=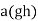
So gh commutes with aa and thus gh∈CG(a).
Thus CG(a) is closed under multiplications.
Let g∈CG(a). This means that we have ga=ag.
Multiplying by g−1 on the left and on the right, we obtain
And thus we have
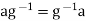
This implies that g−1∈CG(a), hence CG(a) is closed under inverses.
Therefore, CG(a) is a subgroup of G.