Unit - 2

Number theoretic functions

Q1) Describe Number Theoretic functions.

A1)

The product of the values of these functions at two reasonably prime integers equals the product of the values of the functions at these integers. We begin by proving a few multiplicative function theorems that we will utilise later. Then we look at special functions and show that the previously seen Euler -function is truly multiplicative. The sum of divisors and the number of divisors functions are also defined. Define the Mobius function afterwards, which looks at integers in terms of their prime decomposition. The sum of the values of ff at the divisors of a given integer n is the summatory function of a given function. The Mobius inversion of this function is then found, which writes the values of ff in terms of the summatory function's values. We will conclude this chapter by presenting integers with intriguing features and proving some of them.

The set N of positive integers is the domain of definition for an arithmetic function.

An arithmetic function ff is called multiplicative if f(ab)=f(a)f(b) for all a,b∈N such that (a,b)=1.

An arithmetic function ff is called completely multiplicative if

f(ab)=f(a)f(b)(4.1.1)

For all positive integers a,b.

The function f(a)=1 where kk is a completely multiplicative function since

f(ab)=1=f(a)f(b).(4.1.2)

It's also worth noting that a fully multiplicative function is a multiplicative function, but not otherwise.

We'll now show a multiplicative function theorem. The features of multiplicative functions, rather than entirely multiplicative functions, will be of importance to us.

Given a multiplicative function f. Let n=∏sk=1pakk spkak be the prime factorization of n. Then

f(n)=∏k=1sf(pakk).(4.1.3)

By induction on the number of primes in the factorization of nn, we prove this theorem. Assume that n=pa1. As a result, the outcome is straightforward. Assume for a moment that

n=∏k=1spakk,(4.1.4)

We have

f(n)=∏k=1sf(pakk).(4.1.5)

So we have to prove that if

n=∏k=1s+1pakk,(4.1.6)

Then

f(n)=∏k=1s+1f(pakk).(4.1.7)

Notice that for

n=∏k=1s+1pakk,(4.1.8)

We have (∏sk=1pakk,pas+1s+1)=1(∏k=1spkak,ps+1as+1)=1.

Thus we have get

f(n)=f(∏k=1s+1pakk)=f(∏k=1spakk)f(pas+1s+1)(4.1.9)

Which by the inductive step gives

f(∏k=1s+1pakk)=f(n)=∏k=1s+1f(pakk).(4.1.10)

We can see from the preceding theorem that knowing the value of a multiplicative function at the primes in the prime factorization of a number will suffice to evaluate it at an integer.

Q2) Explain Number Of divisors in brief.

A2)

The prime factorization of a divisor d must be a subset of the prime factorization of nn, for example, 6=23 is a divisor of 60=22355. So all we have to do now is find all the different subsets of n's prime factorization.

For a collection of x elements, the number of subsets is usually 2x. If the set contains repeated entries, however, this is no longer the case. Some prime factors may appear more than once in the prime factorization of n in our situation.

We can utilise the factor pp up to e times in the subgroup if a prime factor p appears e times in the prime factorization of nn. As a result, we have e+1 options.

As a result, if n's prime factorization is pe11pe22pekk, with pipi being separate prime integers, the number of divisors is:

d(n)=(e1+1)⋅(e2+1)⋯(ek+1)

A way of thinking about it is the following:

• If n=pe11n=p1e1 is the sole distinct prime divisor, then there are e1+1 divisors (1,p1,p21,...,pe11).

• If there are two distinct prime divisors, n=pe11pe22, then all divisors can be arranged in a tabular format.

	1			…
1	1			…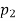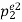
				…
				…
:	:	:	:		:
				…

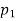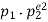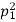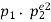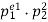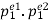• So the number of divisors is trivially (e1+1)⋅(e2+1)
• A similar argument can be made if there are more then two distinct prime factors.

Sum of divisors

The argument from the previous section can be utilised again.

The sum is: n=pe11 if there is just one distinct prime divisor.

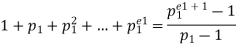
If there are two distinct prime divisors n=pe11⋅pe22, then we can make the same table as before. The only difference is that now we now want to compute the sum instead of counting the elements. It is easy to see, that the sum of each combination can be expressed as:

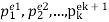• For n= we get the following formula:

Q3) Explain Multiplicative function with Theorem.

A3)

An arithmetical function, or number-theoretic function is a complex-valued function defined for all positive integers. It can be viewed as a sequence of complex numbers.

Examples: n!,ϕ(n),π(n) which denotes the number of primes less than or equal to n.

If f(mn)=f(m)f(n) whenever gcd(m,n)=1, an arithmetical function is multiplicative, and if this holds for any m,n, it is entirely multiplicative or completely multiplicative. Thus, unless f is the zero function, f(1)=1, and the behaviour of a multiplicative function on prime powers is totally specified.

Examples: We saw that the Euler totient function is multiplicative but not completely multiplicative (which is why (1)=1) is useful). n2 is a completely multiplicative function. It is (completely) multiplicative to combine (totally) multiplicative functions.

Theorem: Let f(n) be a multiplicative function, and define

F(n)=∑d|nf(d).

Then F(n) is also a multiplicative function.

Proof: Let m,n be positive integers with gcd(m,n)=1. Then

F(mn)=∑d|mnf(d)=∑r|m,s|nf(rs)=∑r|m,s|nf(r)f(s)=∑r|mf(r)∑s|nf(s)=F(m)F(n)

Since r|m and s|n implies (r,s)=1.

We just wrote F(n) in terms of f(d). Can we do the reverse? That is, write f(n) in terms of F(d)? Yes; this is known as Möbius inversion.

Since ϕ is multiplicative, we have that

Theorem:

∑d|nϕ(n)=n

This theorem can also be proved using basic facts about cyclic groups.

Examples: The divisors of 12 are 1,2,3,4,6,12. Their totients are 1,1,2,2,2,4 which sum to 12.

The function f(n)=1 is (totally) multiplicative. Let d(n) be the number of divisors of n. Then since d(n)=∑d|n1 we see that d(n) is multiplicative.

The function f(n)=n is (totally) multiplicative. Let σ(n) be the sum of divisors of n. Then since σ(n)=∑d|nn we see that σ(n) is multiplicative. In general, we can apply this trick to any power of n.

Q4) State the definition and function of the Dirichlet product.

A4)

Definition

If {\displaystyle f,g:\mathbb {N} \to \mathbb {C} }  are two arithmetic functions from the positive integers to the complex numbers, the Dirichlet convolution f ∗ g is a new arithmetic function defined by:

Where the sum encompasses all positive divisors d of n, or alternatively, all different pairs (a, b) of positive integers whose product is n.

The study of Dirichlet series, such as the Riemann zeta function, naturally produces this product. In terms of their coefficients, it explains the multiplication of two Dirichlet series:

Functions.

The following is a complete list of commonly studied arithmetic functions:

Arithmetic functions is a category of arithmetic functions.

The following are a few of the most important:

• The identity element for Dirichlet product: Denoted I, this is the indicator function for 1: it is 1 at 1 and 0 elsewhere.
• The all ones function: This function sends everything to 1. This is denoted by U. Note that although this is the identity for pointwise multiplication, it is not the identity for the Dirichlet product.
• The Mobius function: Denoted , this is the inverse of the all ones function with respect to the Dirichlet product.
• The identity function: This function sends every natural number to itself, now viewed as a ring element. This is denoted E. Although this would be the identity for composition, it is not the identity for the Dirichlet product.

Q5) What is Mobius Inversion Formula.

A5)

Suppose for some (not necessarily multiplicative) number-theoretic function f

F(n)=∑d|nf(d).

Can we make f(n) the subject of this equation?

We’ll see that we can find a function μ such that

f(n)=∑d|nμ(n/d)F(d)=∑d|nμ(d)F(n/d).

And we call this process Möbius inversion.

We have

∑d|nμ(d)F(n/d)=∑d|nμ(d)∑r|ndf(r)=∑dr|nμ(d)f(r)=∑r|nf(r)∑d|(n/r)μ(d)

If we want this equal to f(n) we need μ to satisfy

∑d|mμ(d)={0,m>11,m=1

A little thought leads to this unique solution, known as the Möbius function:

μ(n)={1n=10p2|n for some prime p(−1)rn=p1...pr for distinct primes pi

Notice μ is multiplicative, which implies f(n) is multiplicative if F(n) is. In summary,

Theorem:

F(n)=∑d|nf(d)

If and only if

f(n)=∑d|nμ(n/d)F(d)

And f(n) is multiplicative if and only if F(n) is multiplicative.

Example: From before n=∑d|nϕ(n). Write n=p1k1...pmkm. Then

ϕ(n)=∑d|nμ(d)nd=n∑d|nμ(d)1d=n(1−∑i1pi+∑i≠j1pipj−...)=n(1−1p1)...(1−1pm)

Which is another way to derive the formula for ϕ.

Gauss encountered the Möbius function over 30 years before Möbius when he showed that the sum of the generators of Zp∗ is μ(p−1). More generally, if Zn∗ has a generator, then the sum of all the generators of Zn∗ is μ(ϕ(n)). This can be seen by considering the sums of the roots of polynomials of the form xd−1 where d|ϕ(n).

Q6) What is greatest integer function.

A6)

A function that returns a constant number for each specific interval is known as the biggest integer function. An open and closed bracket, [ ], is commonly used to symbolise these functions. These are the integer values of the expression inside the brackets, rounded down. The biggest integer functions are illustrated in the following examples:

• $f(x) = [ -5.678]$
• $g(x) = [-x + 1]$
• $h(x) = [-4x2 – 5]$

We'll find the number's maximum integer value when the expression inside the brackets is only a constant.

Let's start by figuring out how to find the largest integer value of a given number. When looking for the largest integer values, keep the following two rules in mind:

If the number in the brackets is not an integer, the smaller integer closest to the supplied number is returned.

• For example, if we have $f(x) = [-15.698]$, the two closest integers are $-16$ and $-15$. For the greatest integer values, we always choose the smaller integer. This means that $[-15.698] = -16$.

We return the original number if the number inside the brackets is an integer.

• This means that if we have $g(x) = [48]$, the greatest integer value is equal to $48$.

Here are some more examples of the greatest integer values:

Once we've mastered finding the largest integer values, we can use that knowledge to graph the largest integer functions. We'll study why this function is also known as a step function in the next section of this essay.

Q7) How to find the greatest integer value?

A7)

Let's start by figuring out how to find the largest integer value of a given number. When looking for the largest integer values, keep the following two rules in mind:

If the number in the brackets is not an integer, the smaller integer closest to the supplied number is returned.

• For example, if we have $f(x) = [-15.698]$, the two closest integers are $-16$ and $-15$. For the greatest integer values, we always choose the smaller integer. This means that $[-15.698] = -16$.

We return the original number if the number inside the brackets is an integer.

• This means that if we have $g(x) = [48]$, the greatest integer value is equal to $48$.

Here are some more examples of the greatest integer values:

Once we've mastered finding the largest integer values, we can use that knowledge to graph the largest integer functions. We'll study why this function is also known as a step function in the next section of this essay.

Q8) How to graph greatest integer function?

A8)

It's time to learn how to provide the biggest integer function on a $xy$-coordinate system. When graphing any other function, we use the same procedure:

• Create a table of values that meets the function's requirements.

• Draw a graph with these points.

• To construct the function, connect the points with a line or a curve.

But what distinguishes the biggest integer or step function from others? As open and closed points, we're using intervals and endpoints.

• On the smaller integer, there will be a shaded point, and on the larger integer, there will be an unfilled dot.

• Vertical lines will then connect each of these.

• For each interval, the same procedure will be followed.

Let's start by graphing [f(x) = [x]], which we can do by making a table of data first.

We may plot each open and closed dot now that we know the values for each interval. After that, draw a line between each pair of dots. The interval [[0, 1)] will be plotted as follows:

Q9) Explain in short the greatest integer function.

A9)

We now know everything there is to know about the biggest integer function, including its fundamental definition, attributes, and graph.

In the next section, we'll begin working on more complex issues, but first, let's review everything we've learned so far:

• We can use the largest integer functions (also known as step functions) to locate the lower integer value that is near to a given number.

• The graph of the step function can be determined by finding values of $y$ at specific intervals of $x$.

• The graph of the biggest integer functions resembles a staircase step.

• We can graph different functions using the graph of $f(x) = [x]$.

Q10) State the properties of Euler’s phi Function.

A10)

To calculate the Euler totient function for any number, the following qualities are sufficient:

• For any 1qp, gcd(p,q)=11 if p is a prime number. As a result, we have:

ϕ(p)=p−1

• If p is a prime number and k1k1 is true, then there are precisely pk/p divisible by p between 1 and pk. This results in:

ϕ(pk)=pk−pk−1.

• If aa and b are substantially prime, the following is true:

ϕ(ab)=ϕ(a)⋅ϕ(b).

This relationship is not easily discernible. The Chinese remainder theorem proves it. The Chinese remainder theorem ensures that for each 0xa0xa and each 0yb, a unique 0zab with zx(moda) and zy(moda) exists (modb) It's simple to show that z is  coprime to abab if and only if x and y are coprime to aa and b. As a result, the number of integers coprime to ab equals the product of a and b.

• In general, if aa and bb are not coprime, the equation is

ϕ(ab)=ϕ(a)⋅ϕ(b)⋅d

Gcd= (a,b).

As a result, we may get (n) by factorising n using the first three properties (decomposition of n into a product of its prime factors). If n=p1a1p2a2pkak, and the prime elements of n are pi, then

ϕ(n)=ϕ(p1a1)⋅ϕ(p2a2)⋯ϕ(pkak)

=(p1a1−p1a1−1)⋅(p2a2−p2a2−1)⋯(pkak−pkak−1)

=pa11⋅(1−1p1)⋅pa22⋅(1−1p2)⋯pakk⋅(1−1pk)

=n⋅(1−1p1)⋅(1−1p2)⋯(1−1pk)

Q11) State the Eulers Theorem.

A11)

Euler's theorem expresses the most renowned and important property of Euler's totient function:

aϕ(m)≡1(modm)

If a and m are both fairly prime

In the scenario where mm is prime, Euler's theorem is transformed into Fermat's little theorem:

Am−1≡1(modm)

Euler's theorem and Euler's totient function are both used to compute the modular multiplicative inverse, for example.

As a result, we have the following equivalence:

An≡anmodϕ(m)(modm)

This allows you to compute xnmodm for very large n, especially if n is the result of another calculation, because it allows you to compute n as a modulo.

Q12) Elaborate reduced set of residues.

A12)

Modulo mm residue of aa As a result, any integer modulo m is congruent to one of the integers 0,1,2,...,m1.

A full residue system modulo mm is a collection of integers in which each integer is modulo mm congruent with exactly one other integer in the set.

The set of integers 0,1,2,...,m1 is the simplest complete residue system modulo mm. Every integer modulo mm is congruent to one of these integers.

A complete residue system modulo 5 is formed by the set of integers 0,1,2,3,4. 6,7,8,9,10 could be another full residue system modulo 55.

A reduced residue system modulo mm is a collection of integers riri such that (ri,m)=1 for all ii and rirj(mod m) for all ijij.

It's worth noting that eliminating all the components of the entire residue system set that aren't approximately prime to mm yields a reduced residue system modulo mm.

A reduced residue system modulo 6 is the set of integers 1,5.

The lemma that follows can be used to find a complete residue system modulo any positive integer m.

In mathematics, a reduced residue system modulo n is a subset R of the numbers that:

1. Gcd(r, n) = 1 for each r in R,
2. R contains φ(n) elements,
3. No two elements of R are congruent modulo n.[1][2]

The totient function of Euler is denoted by.

A reduced residue system modulo n can be created by deleting all numbers that are not relatively prime to n from a complete residue system modulo n. A full residue system modulo 12 is, for example, 0 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11. The only integers in this set that are relatively prime to 12 are the so-called totatives 1, 5, 7 and 11, hence the corresponding reduced residue system modulo 12 is 1, 5, 7, 11. The totient function can be used to find the cardinality of this set: (12) = 4. Modulo 12 systems with decreased residues include:

• {13,17,19,23}
• {−11,−7,−5,−1}
• {−7,−13,13,31}
• {35,43,53,61}
• If {r1, r2, ... , rφ(n)} is a reduced residue system modulo n with n > 2, then

{\displaystyle \sum r_{i}\equiv 0\!\!\!\!\mod n} .

• A generator for the additive group of integers modulo n is every number in a reduced residue system modulo n.

Q13) Define Number Theoretic Functions.

A13) 

The product of the values of these functions at two reasonably prime integers equals the product of the values of the functions at these integers. We begin by proving a few multiplicative function theorems that we will utilise later. Then we look at special functions and show that the previously seen Euler -function is truly multiplicative. The sum of divisors and the number of divisors functions are also defined. Define the Mobius function afterwards, which looks at integers in terms of their prime decomposition. The sum of the values of ff at the divisors of a given integer nn is the summatory function of a given function. The Mobius inversion of this function is then found, which writes the values of ff in terms of the summatory function's values. We will conclude this chapter by presenting integers with intriguing features and proving some of them.

Q14) Define Euler’s Phi-Function.

A14)

The totient function , also called Euler's totient function, is defined as the number of positive integers  that are relatively prime to (i.e., do not contain any factor in common with) n, where 1 is counted as being relatively prime to all numbers. Since a number less than or equal to and relatively prime to a given number is called a totative, the totient function , can be simply defined as the number of totatives of n. For example, there are eight totatives of 24 (1, 5, 7, 11, 13, 17, 19, and 23), so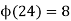 

The totient function is implemented in the Wolfram Language as EulerPhi[n].

The number 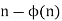, is called the cototient of n and gives the number of positive integers that have at least one prime factor in common with n.

Q15) Define Euler’s Theorem and state the properties.

A15)

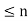The totient function , also called Euler's totient function, is defined as the number of positive integers  that are relatively prime to (i.e., do not contain any factor in common with) n, where 1 is counted as being relatively prime to all numbers. Since a number less than or equal to and relatively prime to a given number is called a totative, the totient function 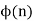, can be simply defined as the number of totatives of n. For example, there are eight totatives of 24 (1, 5, 7, 11, 13, 17, 19, and 23), so 

The totient function is implemented in the Wolfram Language as EulerPhi[n].

The number 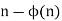, is called the cototient of n and gives the number of positive integers that have at least one prime factor in common with n.

Q16) How to find the greatest integer value and graph greatest integer function?

A16)

Let's start by figuring out how to find the largest integer value of a given number. When looking for the largest integer values, keep the following two rules in mind:

If the number in the brackets is not an integer, the smaller integer closest to the supplied number is returned.

• For example, if we have $f(x) = [-15.698]$, the two closest integers are $-16$ and $-15$. For the greatest integer values, we always choose the smaller integer. This means that $[-15.698] = -16$.

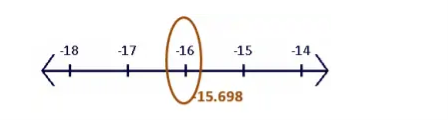
We return the original number if the number inside the brackets is an integer.

• This means that if we have $g(x) = [48]$, the greatest integer value is equal to $48$.

Here are some more examples of the greatest integer values:

Once we've mastered finding the largest integer values, we can use that knowledge to graph the largest integer functions.

Graph:

It's time to learn how to provide the biggest integer function on a $xy$-coordinate system. When graphing any other function, we use the same procedure:

• Create a table of values that meets the function's requirements.

• Draw a graph with these points.

• To construct the function, connect the points with a line or a curve.

But what distinguishes the biggest integer or step function from others? As open and closed points, we're using intervals and endpoints.

• On the smaller integer, there will be a shaded point, and on the larger integer, there will be an unfilled dot.

• Vertical lines will then connect each of these.

• For each interval, the same procedure will be followed.

Let's start by graphing [f(x) = [x]], which we can do by making a table of data first.

We may plot each open and closed dot now that we know the values for each interval. After that, draw a line between each pair of dots. The interval [[0, 1)] will be plotted as follows:

Q17) n!,ϕ(n),π(n) which denotes the number of primes less than or equal to n.

A17)

An arithmetical function is multiplicative if f(mn)=f(m)f(n) whenever gcd(m,n)=1, and totally multiplicative or completely multiplicative if this holds for any m,n. Thus f(1)=1 unless f is the zero function, and a multiplicative function is completely determined by its behaviour on the prime powers.

Q18) The divisors of 12 are 1,2,3,4,6,12. Their totients are 1,1,2,2,2,4 which sum to 12.

A18)

The function f(n)=1 is (totally) multiplicative. Let d(n) be the number of divisors of n. Then since d(n)=∑d|n1 we see that d(n) is multiplicative.

The function f(n)=n is (totally) multiplicative. Let σ(n) be the sum of divisors of n. Then since σ(n)=∑d|nn we see that σ(n) is multiplicative. In general, we can apply this trick to any power of n.

Q19) Show that the Dirichlet inverse of λ is ∣μ∣.

A9)

Both λ and ∣μ∣ are multiplicative, so their Dirichlet convolution λ∗∣μ∣ is multiplicative. Therefore, e is also multiplicative, so it suffices to show that the two functions agree on prime powers. (This important fact is explained in the wiki on multiplicative functions.)

Now,

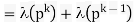
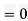
Since e(pk)=0, the functions agree on prime powers and hence are the same.

Q20) Show that d∗φ=σ.

A20)

Start with 1∗φ=I and convolve both sides with 1:

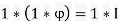
Q21) Show that

A21)

The left side is

Where φ=μ∗I comes from Möbius inversion of φ∗1=I. Rearranging and moving parentheses around gives

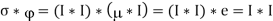
And

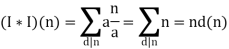
Q22) Find the value of x such that ⌊x+3⌋ = 3

A22)

From the definition of the greatest integer function, we have 3 ≤ x+1 < 4

Subtract 1 in this inequality.

We get, 2 ≤ x < 3

x can take the values greater than or equal to 2 and less than 3.

Q23) What is the domain of the given greatest integer functions:

a) f(x)=1/⌊x⌋

(b) g(x)=1{x}?

A23)

(a) The denominator should not be 0, that is, ⌊x⌋≠0

The greatest integer part of a number is 0 if that number lies in the interval [0,1)

Thus, to obtain the domain, this interval must be excluded from the set of real numbers.

This means that the domain of f is R−[0,1)

(b) Once again, the denominator should not be 0, which means that {x}≠0

When is the fractional part of a number equal to 0?

Only when that number is an integer!

Thus, the domain of g is R−Z, that is, all integers have been excluded from the set of real numbers.

A) The domain of f is R−[0,1) and the domain of g is R−Z.

Q24) Which of the following cannot be the value of [ 3√1 ] + [ 3√2 ] + [ 3√3 ] + ........+ [ 3√n > ] ?

A24)

Breaking the problem into steps,

• The value of [ 3√1 ] is 1 and it will remain 1 till [ 3√7 ] as cube of 2 is 8, so [ 3√8 ] = 2. Hence, the sum of first 7 terms is 7.
• The values of each term from [ 3√8 ] to [ 3√26 ] is 2. The sum of these 19 terms is 38. The sum of all the 26 terms will be 7 + 38 = 45.
• It also implies that for 7 < n < 27, the sum of these terms will be 7 + 2k. That means the sum 37, which is of this form only is definitely possible. So, the first option is possible.
• From [ 3√27 ] to [ 3√63 ], each of the 37 terms has value 3 and their total will be 111. Now total up to this point is 156. Hence, 153 is also possible.
• Now, [ 3√64 ] = 4 and the value of next 61 terms will be 4 each. That also means the sum for n > 63 will be 156 + 4k.

Now, 188 is a number of this form and is possible and 190 is not possible as it cannot be written in the form of 156 + 4k. Hence, we have successfully identified the answer.

Q25) Find the value of [√1 ] + [√2 ] + [√3 ] + [√4 ] + ..... + [√24 ], where [x] is the greatest integer less than or equal to x.

A25)

Here from [ √1 ] to [ √3 ] each term has value 1, as the square root of all these numbers will be greater than equal to 1 but less than 2. The greatest integer less than those will be 1. So, the total of these three terms will be 3.

• The value of each term from [ √4 ] to [ √8 ] is 2 on the base of the same logic as explained above, so the total of these 5 terms is 10.
• From [√9 ] to [ √15], the value of each term is 3 and total of these 7 terms is 21.
• Similarly, the value of each term from [ √16 ] to [ √24 ] is 4 and the sum of these 9 terms is 36.

So, we have [√1 ] + [√2 ] + [√3 ] + [√4 ] + ..... + [√24 ] = 3 + 10 + 21 + 36 = 70.